Лабораторная работа №7 исследование преобразования сигналов безынерционными нелинейными звеньями

Цель работы: Изучить преобразовательные свойства безынерционных нелинейных звеньев.

Задачи работы:

1. Исследовать преобразования регулярных сигналов безынерционными нелинейными звеньями.

1. Исследовать прохождение стационарных случайных процессов через безынерционные нелинейные звенья.

ВВЕДЕНИЕ.

Нелинейные элементы, используемые в технике связи и имеющие "гладкие" статические характеристики обычно описываются степенным рядом

.

Так как интерес представляет, как правило, изменение сигнала – постоянная составляющая из рассмотрения исключается. Для уменьшения сложности вычислений, во внимание принимаются слагаемые со степенью, не выше второй. С учетом этого:

В спектральной области входному сигналу соответствует сигнал на выходе нелинейного элемента

Классическим сигналом, прохождение через нелинейность которого, исследуется, является сигнал с ограниченным равномерным спектром

здесь

Спектр мощности квадратичной составляющей выходного сигнала имеет вид:

,

где

- константа, определяемая шириной спектра входного сигнала.

Результирующий спектр мощности выходного сигнала будет иметь вид

Классическими регулярными сигналами, прохождение через нелинейность которых исследуется, являются гармонический сигнал и сумма двух гармонических компонент с различными частотами.

.

Для гармонического входного сигнала на выходе нелинейного звена имеем:

из чего видно, что выходной сигнал приобретает дополнительно постоянную составляющую и вторую гармонику. Если на входе нелинейного звена действует сигнал, содержащий две гармонические компоненты, то

Из вышеприведенного соотношения следует, что наряду с дополнительной постоянной составляющей и компонентами удвоенной частоты выходной сигнал имеет компоненты с суммарной и разностной частотами, являющимися продуктами взаимодействия двух гармонических компонент входного сигнала на нелинейности.

Такое взаимодействие в реальной системе связи может привести к негативным последствиям – появлению нежелательных компонент в спектре выходного сигнала. Другим негативным следствием упомянутого взаимодействия сигналов может быть подавление слабого сигнала сильным. Рассмотренные выше эффекты в нелинейных звеньях используются также и с положительным результатом в умножителях частоты, смесителях и т.д.

Примером "негладкой" (существенной) нелинейности является нелинейность типа "ограничение" (см. рис. 7.1).

Звеном с такой характеристикой обычно моделируют усилители, ограничители сигналов и т.д.

Нелинейные свойства в большей или меньшей мере обнаруживаются практически во всех элементах электронных схем, и они оказывают существенное влияние на работу устройств каналов связи. В одних случаях нелинейные свойства совершенно необходимы для обеспечения преобразования сигналов (детектор огибающей, умножитель частоты), в других – оказывают негативное влияние на работу устройств, которые по своему назначению должны быть линейными. В каждом из таких приложений возникает необходимость воздействовать на параметры элементов с целью получения наилучшего результата.

В данной лабораторной работе в качестве устройства, реализующего преобразовательные свойства нелинейности, рассматривается детектор огибающей. Здесь за счет оптимизации параметров нелинейности, параметров сигналов и параметров линейных звеньев, входящих в состав устройства, стремятся наилучшим образом использовать нелинейность для достижения наибольшего значения коэффициента преобразования, наибольшего соотношения сигнал-шум и т.д.

Примером другого класса устройств, рассматриваемых в данной работе, является радиочастотный усилитель, который по своему назначению является линейным устройством. Однако, в силу наличия даже слабых нелинейностей активных элементов (транзисторов, ИМС, электронных ламп) и действии на его входе сигналов значительного уровня, он может быть источником интермодуляционных помех и паразитных каналов приема. Упрощенные схемы вышеназванных устройств приведены на рисунках 7.2 и 7.3.

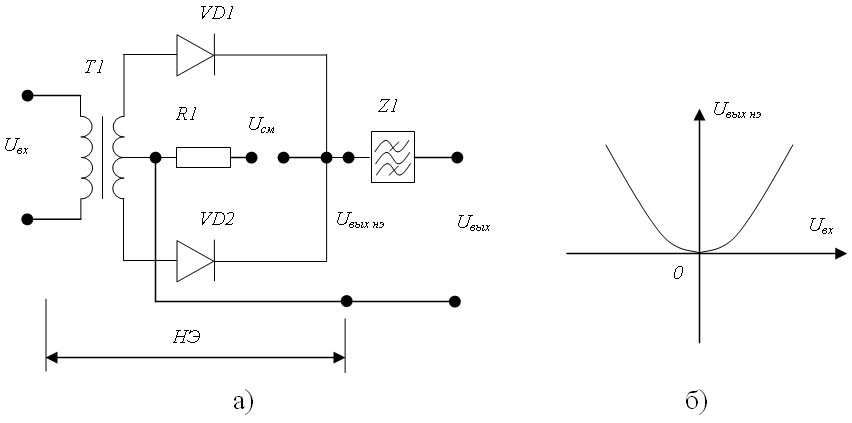
Рисунок 7.2 – Детектор огибающей а) и статическая характеристика нелинейного элемента б).

Рисунок 7.3. – Радиочастотный усилитель а) и статическая характеристика эквивалентной нелинейности б).

В состав устройств кроме нелинейного элемента, представленного диодами или транзисторами, входят цепи подачи начального смещения, позволяющие задавать нужный режим работы нелинейного элемента, цепи согласования, обеспечивающие наилучшие условия передачи мощности сигнала в нелинейный элемент и от него в нагрузку, и полосовые фильтры, определяющие границы спектров сигналов.

ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ

В первой части лабораторной работы исследуются общие свойства нелинейных звеньев. Объектом исследования в данной работе является простейшая структура (см. рис. 7.4), содержащая нелинейные элементы с рассмотренными выше характеристиками, источники входных сигналов и регистраторы. В качестве входных сигналов используются гармонические сигналы, Гауссов белый шум и сигнал с равномерным спектром ограниченным по частоте. Последний сигнал получается путем пропускания импульса (δ-функции) через фильтр низких частот, форма АЧХ которого стремится к идеальной. Задачи данной части работы реализуются путем анализа в частотной области выходных сигналов нелинейностей при действии различных сигналов на входе.

Во второй части лабораторной работы рассматриваются модели двух узлов канала связи (детектора огибающей и усилителя), на работу которых значительное влияние оказывают нелинейные свойства их элементов.

Несмотря на заметное различие схем устройств, они могут быть промоделированы в пакете SystemView с помощью моделей имеющих общую основу и включающих источники сигналов, собственно нелинейность, фильтры, а так же средства регистрации и обработки результатов моделирования. Различия состоят в используемых входных сигналах, параметрах нелинейности и фильтров, измеряемых величинах, обработке и интерпретации результатов измерений.

Так при исследовании детектора огибающей источником входного сигнала является амплитудный модулятор, а задача исследования состоит в оценке качества восстановления передаваемого сообщения, представленного гармоническим сигналом, при использовании различных видов нелинейностей и для различных параметрах сигналов. В качестве показателей качества здесь могут быть использованы коэффициент нелинейных искажений восстановленного сигнала

где – мощность -ой гармоники выходного сигнала в абсолютных единицах измерения (в Вт),

и потери детектирования

,

где – соотношение сигнал шум на входе и выходе детектора огибающей в децибелах.

При исследовании усилителя со слабой нелинейностью задача состоит в оценивании защищенности усилителя от паразитного влияния на его работу внеполосных сигналов значительного уровня. Входным сигналом в этом исследовании является двухтоновый сигнал

.

Здесь одна из компонент, например, с частотой считается полезным сигналом, а вторая, с близкой ей частотой – помехой. В качестве показателя защищенности усилителя от действия сигналов значительного уровня можно использовать уровень сигнала на входе усилителя, при котором на выходе усилителя мощность интермодуляционной компоненты второго порядка с частотой

или компоненты третьего порядка с частотой

или

сравняются с мощностью полезной усиленной компоненты с частотой .