2.6. Фундаментальная последовательность. Критерий Коши сходимости последовательности

Определение 1. Последовательность называется фундаментальной, если такое, что и выполняется неравенство .

Это определение эквивалентно следующему.

Определение 2. Последовательность называется фундаментальной, если такое, что и выполняется неравенство .

Геометрически это означает, что если последовательность фундаментальна, то такое, что расстояние между любыми двумя членами последовательности с номерами, бóльшими, чем , меньше .

Теорема (критерий Коши). Для того, чтобы последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.

Доказательство необходимости.

Пусть последовательность {x_n} сходится и . Зададим ε>0, тогда, согласно определению предела последовательности, существует такое n_ε , что для всех n≥n_ε выполняется неравенство ││<. Пусть теперь n≥n_ε и m≥n_ε, тогда │х_n–x_m│=│(x_n–a)+(x_m–a)│≤│x_n–a│+│x_m–a│<+=ε, т.е. выполняется условие Коши.

Доказательство достаточности.

Пусть последовательность {x_n} удовлетворяет условию Коши, т.е. для всякого ε>0 существует такое n_ε, что если n≥n_ε и m≥n_ε, то │х_n–x_m│<ε. Возьмём для примера ε=1,тогда существует такое что при n≥n₁ и m≥n₁ выполняется неравенство │х_n-x_m│<1 ,т.е. при n≥n₁.Это значит, что последовательность x_n, n=n₁, n₁+1,… ограничена. Поэтому в силу теоремы 4 Больцано-Вейерштрасса (см. 2.2) существует ее сходящаяся подпоследовательность {}.

Пусть . Покажем, что вся данная последовательность {x_n} также сходится и имеет пределом число a. Зададим ε>0. Тогда, во-первых, по определению подпоследоваельности, для всех выполняется неравенство │–a│< <. Во-вторых, так как последовательность {x_n} удовлетворяет условию Коши, то существует такое n_ε, что для всех n≥n_ε и m≥n_ε выполняется неравенство │х_n–x_m│<.

Положим N_ε=max{n_ε, } и зафиксируем некоторое n_k≥N_ε. Тогда для всех n≥ N_ε получим: │x_n–a│=│(x_n–)+(– –a)│≤ │x_n–│+│–a│<+=ε, а это и доказывает, что .

Пример 1. Пользуясь критерием Коши, доказать сходимость последовательности , где .

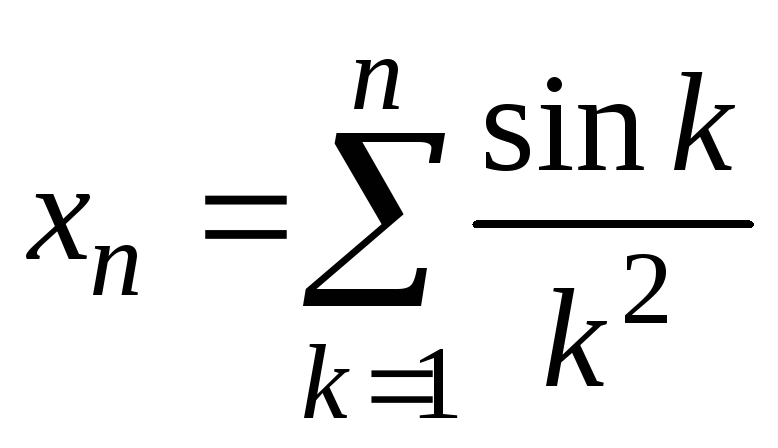Решение. В силу критерия Коши достаточно доказать, что последовательность – фундаментальная. Для этого оценим . Имеем .

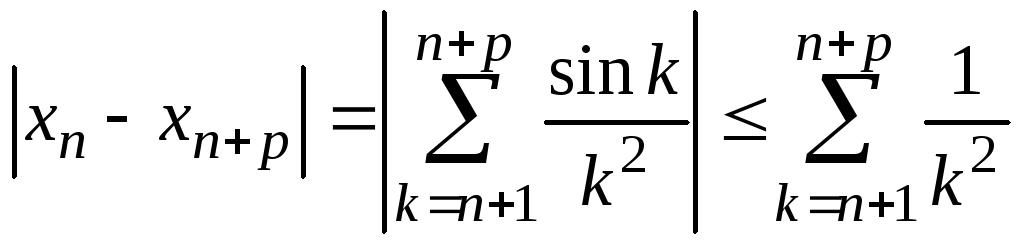Так как , то

.

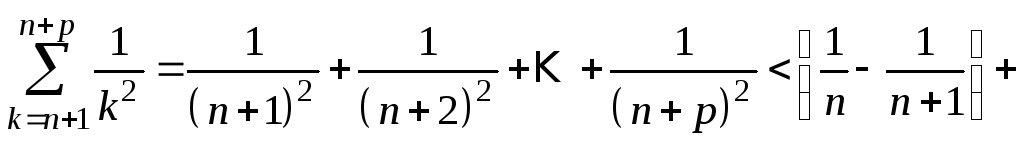
Поэтому имеем

. (*)

Зададим теперь произвольное и положим . Тогда выполняется неравенство , откуда . Следовательно, и , используя неравенство (*), получаем . Это доказывает фундаментальность последовательности , а значит и ее сходимость.

Пример 2. Пользуясь критерием Коши, доказать расходимость последовательности , где .

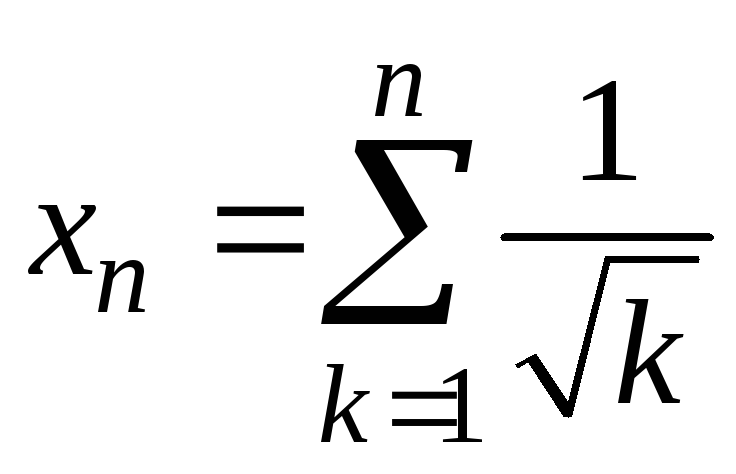Решение. В силу критерия Коши достаточно доказать, что последовательность не является фундаментальной. Для этого оценим . Имеем

.

В частности, при получаем . Возьмем . Тогда такие, что . В самом деле, в силу доказанного неравенства достаточно взять любое и . Это доказывает, что последовательность не является фундаментальной, а, следовательно, она расходящаяся.

2.7. Предельные точки последовательности. Верхний и нижний пределы

Пусть - некоторая числовая последовательность. Рассмотрим произвольную возрастающую последовательность целых положительных чисел (). Выберем из члены с номерами :

.

Полученная числовая последовательность называется подпоследовательностью последовательности .

Теорема 1. Если , то любая подпоследовательность сходится к при .

Определение 1. Число называется предельной точкой (или частичным пределом) последовательности , если из последовательности можно выделить подпоследовательность , сходящуюся к .

Сравните с определением 6 из п. 1.7.

Можно и по другому сформулировать определение предельной точки.

Определение 2. Число называется предельной точкой последовательности , если в любой -окрестности точки содержится бесконечно много членов последовательности .

На языке последовательностей теорема 1 из п. 1.6. формулируется так.

Теорема 2 (Больцано-Вейерштрасса). Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Из теоремы 1 следует, что сходящаяся последовательность имеет только одну предельную точку, совпадающую с ее пределом.

Из теоремы 2 следует, что всякая ограниченная последовательность имеет, по крайней мере, одну предельную точку.

Определение 3. Наибольшая (наименьшая) предельная точка последовательности , ограниченной сверху (снизу), называется верхним (нижним) пределом этой последовательности и обозначается .

Очевидно, если сходится, то . Если последовательность не ограничена сверху (снизу), то полагают .

Пример 1. Доказать расходимость последовательности .

Решение. Рассмотрим две подпоследовательности этой последовательности и (). Очевидно, что , . Таким образом, последовательность имеет две предельные точки: и , а поэтому не может быть сходящейся, поскольку сходящаяся последовательность имеет только одну предельную точку.

Пример 2. Найти все предельные точки последовательности , верхний и нижний пределы этой последовательности.

Решение. Каждое из чисел , , , , , встречается в последовательности бесконечно много раз, поскольку . Поэтому каждое указанное число является предельной точкой последовательности . Других предельных точек последовательность не имеет, так как если число не совпадает ни с одним из этих 181 чисел, то существует окрестность точки , не содержащая ни одного члена последовательности. Из найденных 181 предельных точек наименьшей является , а наибольшей 1, т.е. , .