2.5. Признак сходимости ограниченной монотонной последовательности. Число «е» как предел последовательности рациональных чисел

Определение 1. Последовательность называется ограниченной сверху (снизу), если такое, что .

Определение 2. Последовательность называется ограниченной, если такое, что .

С геометрической токи зрения это означает, что все члены последовательности находятся в некоторой окрестности (-окрестности) точки .

Определение 3. Последовательность называется неограниченной, если такое, что .

Пример 1. Докажем, что последовательность с общим членом ограничена.

Решение. Мы имеем , поэтому

.

Это означает, что заданная последовательность ограничена и сверху и снизу, т.е. является ограниченной.

Определение 4. Последовательность называется строго возрастающей, если , и строго убывающей, если .

Пример 2. Докажем, что последовательность с общим членом возрастает.

Решение. Мы имеем , поэтому

.

Так как , то для всех выполняется неравенство , значит возрастает.

Определение 5. Последовательность называется невозрастающей (неубывающей), если .

Все такие последовательности называют монотонными. Монотонные последовательности всегда ограничены хотя бы с одной стороны: невозрастающая последовательность ограничена сверху, а неубывающая последовательность – снизу своим первым членом. Если же монотонная последовательность ограничена и с другой стороны, то она сходится.

Теорема 2 (Вейерштрасс). Монотонная ограниченная последовательность имеет предел.

Доказательство: Пусть {a_n} неубывающая и ограниченная сверху последовательность. Так как она ограничена сверху, то существует sup{a_n}. Пусть s =sup{a_n}. Покажем, что . По определению верхней грани для любого ε>0 существует номер N такой, что Поскольку последовательность неубывающая, при любом nN получаем т.е. что и требовалось доказать.

Пример 3. Важнейшим примером применения признака Вейерштрасса является доказательство существования предела последовательности

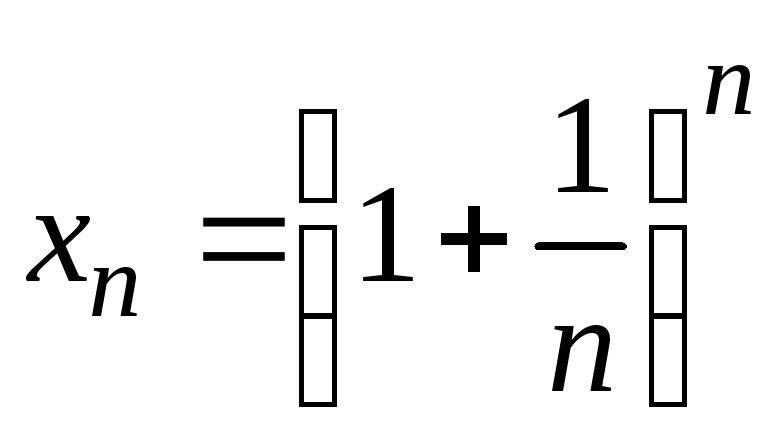, n N (1)

Покажем, что данная последовательность является монотонной и ограниченной сверху.

Решение. По формуле бинома Ньютона

(a+b)ⁿ=aⁿ+a ^n-1 ·b+^n-2·b²+…ⁿ

Полагая a=1, b=, получим

ⁿ=1+

=1+1+

или

ⁿ=1+1+ (2)

Из равенства (2) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины (1-), (1-), …возрастают. Поэтому последовательность{x_n}= -возрастающая, при этом

(1+)ⁿ >2 (3)

Покажем что она ограничена. Заменим каждую скобку в правой части равенства (2) на единицу; правая часть увеличится, получим неравенство

<1 +1+

Усилим полученное неравенство, заменив числа 3, 4, 5,…, стоящие в знаменателях дробей, числом 2:

<1 +

Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:

1+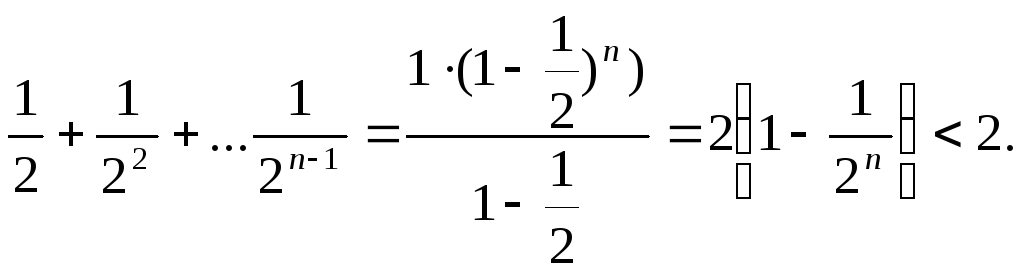

Поэтому <1 + 2=3 (4)

Итак, последовательность ограниченна, при этом для выполняются неравенства (3) и (4):

2<< 3

Следовательно, на основании теоремы Вейерштрасса последовательность

x_n=, nN, имеет предел, обозначаемый обычно буквой е:

Поскольку и последовательность (1) строго возрастает, то . Можно показать, что число – иррациональное и даже трансцендентное, т.е. оно не является корнем никакого уравнения с целыми коэффициентами.