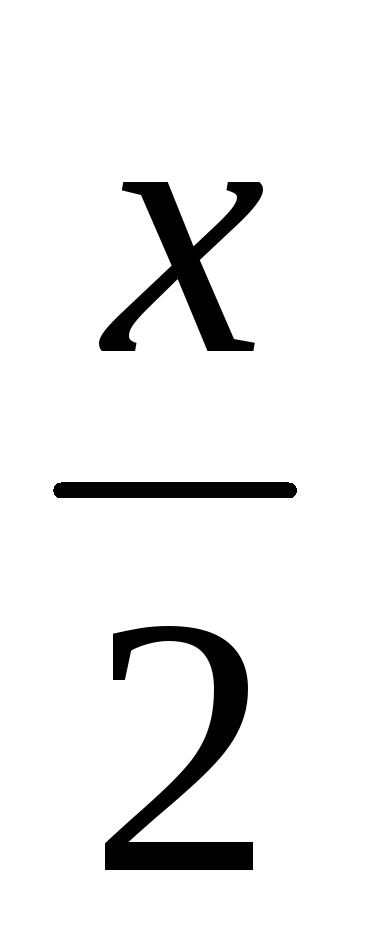- •Лекция №7 предел функции
- •4.1. Определения предела функции в точке.Теорема об эквивалентности определений. Односторонние пределы.
- •4.2. Бесконечно малые функции, их свойства. Бесконечно большие функции
- •4.3. Основные теоремы о пределах
- •4.4. Признаки существования пределов
- •Раскрытие некоторых неопределенностей
- •4.5. Критерий Коши
- •4.6 Сравнение бесконечно малых функций
- •Вычислить пределы функций.
- •4. Задачи Группа а
- •Группа б
- •Группа в
4.6 Сравнение бесконечно малых функций
Если
функции
![]() и
и
![]() бесконечно малы при
бесконечно малы при
![]() ,
то
,
то
![]() (неопределенность вида
(неопределенность вида
![]() )
может равняться либо нулю, либо
бесконечности, либо какому-нибудь числу,
отличному от нуля; наконец, он может не
существовать.
)
может равняться либо нулю, либо
бесконечности, либо какому-нибудь числу,
отличному от нуля; наконец, он может не
существовать.
Если
![]() ,
то при
,
то при
![]() функция
функция
![]() быстрее стремится к нулю, чем
быстрее стремится к нулю, чем
![]() .
Говорят, что
.
Говорят, что
![]() – бесконечно малая
более высокого порядка, чем
– бесконечно малая
более высокого порядка, чем
![]() .
Пишут
.
Пишут
![]() .
.
Если
![]() ,
то
,
то
![]() – бесконечно малая
более низкого порядка, чем
– бесконечно малая
более низкого порядка, чем
![]() .
Пишут
.
Пишут
![]() .
.
Если
![]() ,
то
,
то
![]() и
и
![]() – бесконечно малые
одного порядка, чем
– бесконечно малые
одного порядка, чем
![]() .
Пишут
.
Пишут
![]() и
и
![]() .
.
Особенно
важен частный случай, когда
![]() .
В этом случае
.
В этом случае
![]() и
и
![]() называются эквивалентными
бесконечно малыми (при
называются эквивалентными
бесконечно малыми (при
![]() ).
Пишут
).
Пишут
![]() .
.
Если
![]() не существует, то
не существует, то
![]() и
и
![]() называют несравнимыми
бесконечно малыми.
называют несравнимыми
бесконечно малыми.
Функция
![]() при
при
![]() называется бесконечно
малой первого порядка.
Если
называется бесконечно
малой первого порядка.
Если
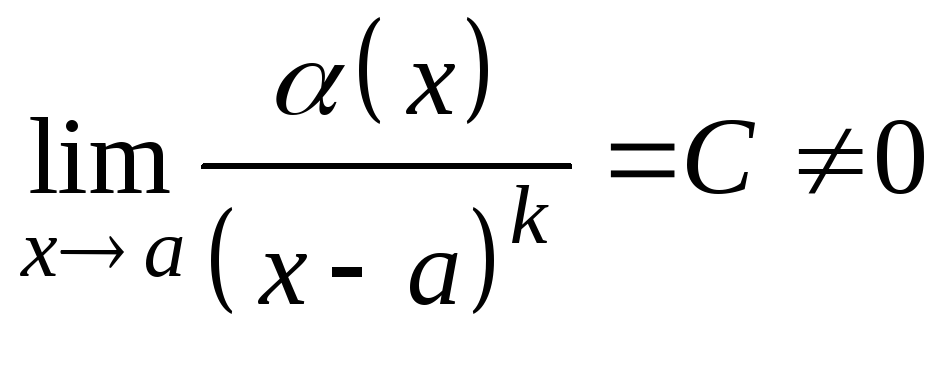 ,
то бесконечно малую
,
то бесконечно малую
![]() называют бесконечно
малой порядка
называют бесконечно
малой порядка
![]() .
.
Пример
1. Вычислить предел
![]() .
.
Решение.
Так как
![]() ,
а из первого замечательного предела
следует
,
а из первого замечательного предела
следует
![]() ,
то имеем
,
то имеем
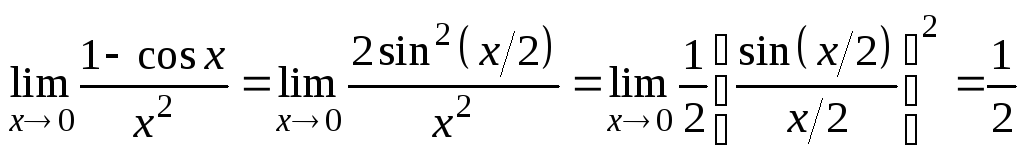 .
.
Поэтому
![]() и
и
![]() – эквивалентные бесконечно малые при
– эквивалентные бесконечно малые при
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() – бесконечно малая второго порядка по
сравнению с
– бесконечно малая второго порядка по
сравнению с
![]() .
.
Из первого
замечательного предела, его следствий
и следствий из второго замечательного
предела следует при
![]() эквивалентность следующих функций
эквивалентность следующих функций
x~sinx~tgx~arctgx~ln(1+x) ~ex-1
Пример
2. Показать, что бесконечно малые
величины
![]() и
и
![]() при
при
![]() являются эквивалентными.
являются эквивалентными.
Решение:
Рассмотрим
![]()
Пример
3. Показать, что бесконечно малые
величины
![]() и
и
![]() при
при
![]() являются эквивалентными.
являются эквивалентными.
Решение:
Рассмотрим
Теорема 1.
Для того чтобы функции
![]() и
и
![]() были эквивалентными при
были эквивалентными при
![]() ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
![]() .
.
Необходимость:
Пусть f
эквивалентно g при x![]() ,
т.е α(x)=φ(x)β(x),
где
,
т.е α(x)=φ(x)β(x),
где
![]() .
Тогда α(x)- β(x)= φ(x) β(x)- β(x)=[ φ(x)-1] β(x)=ε(x)
β(x), где ε(x)=[ φ(x)-1]
.
Тогда α(x)- β(x)= φ(x) β(x)- β(x)=[ φ(x)-1] β(x)=ε(x)
β(x), где ε(x)=[ φ(x)-1]![]() 0
при x
0
при x![]() ,
т.е имеем
,
т.е имеем
![]()
Достаточность:
Пусть выполняется
![]() ,
т.е α(x)= β(x)+ε(x)
β(x), где
,
т.е α(x)= β(x)+ε(x)
β(x), где
![]() .
Тогда α(x)= β(x)[1+ε(x)]=
φ(x)β(x),где
φ(x)= 1+ ε(x)
.
Тогда α(x)= β(x)[1+ε(x)]=
φ(x)β(x),где
φ(x)= 1+ ε(x)
![]() 0
при x
0
при x![]() ,т.е.
f эквивалентно g
при x
,т.е.
f эквивалентно g
при x![]() ,
,
Это условие можно записать
в виде
![]() .
Оно означает, что разность эквивалентных
бесконечно малых является бесконечно
малой более высокого порядка.
.
Оно означает, что разность эквивалентных
бесконечно малых является бесконечно
малой более высокого порядка.
При вычислении пределов весьма полезной оказывается следующая теорема.
Теорема 2.
Если при
![]() функции
функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() бесконечно малы и a1~a,
β1~β, то
бесконечно малы и a1~a,
β1~β, то
![]() ,
Условие эквивалентности функций f
и f1 при
х стремящемся к х0 означает, что
f(x)=φ(x)
f1(х),
где
,
Условие эквивалентности функций f
и f1 при
х стремящемся к х0 означает, что
f(x)=φ(x)
f1(х),
где
![]() ,
а условие эквивалентности функций g
и g1 при х стремящемся
к х0- что g(x)=ψ(x)g1(х),
где
,
а условие эквивалентности функций g
и g1 при х стремящемся
к х0- что g(x)=ψ(x)g1(х),
где
![]() .
Кроме того, поскольку существует предел
.
Кроме того, поскольку существует предел
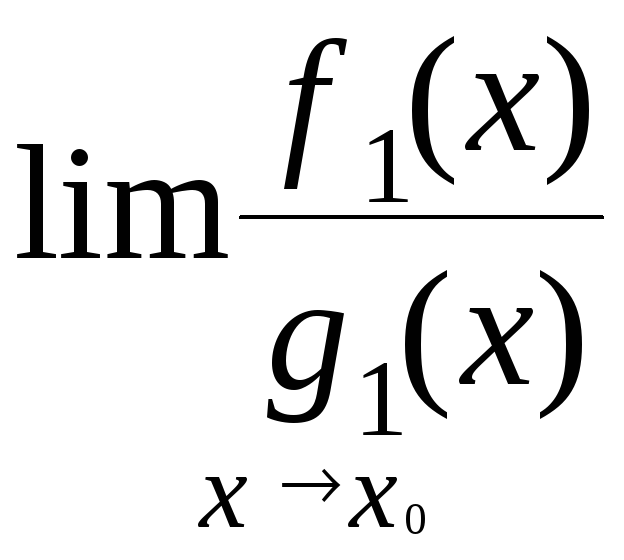 ,
функция
,
функция
![]() определена в некоторой проколотой
окрестности точки х0 и , следовательно,
всюду в этой окрестности выполняется
неравенство g1(х)
определена в некоторой проколотой
окрестности точки х0 и , следовательно,
всюду в этой окрестности выполняется
неравенство g1(х)![]() 0.
Поскольку g(x)=ψ(x)g1(х),
и, очевидно, ψ(x)
0.
Поскольку g(x)=ψ(x)g1(х),
и, очевидно, ψ(x)
![]() 0
в некоторой проколотой окрестности
точки х0, то функция g(x)
обладает тем же свойством. Поэтому
функция
0
в некоторой проколотой окрестности
точки х0, то функция g(x)
обладает тем же свойством. Поэтому
функция
![]() определена в некоторой проколотой
окрестности точки х0.Теперь имеем:
определена в некоторой проколотой
окрестности точки х0.Теперь имеем:
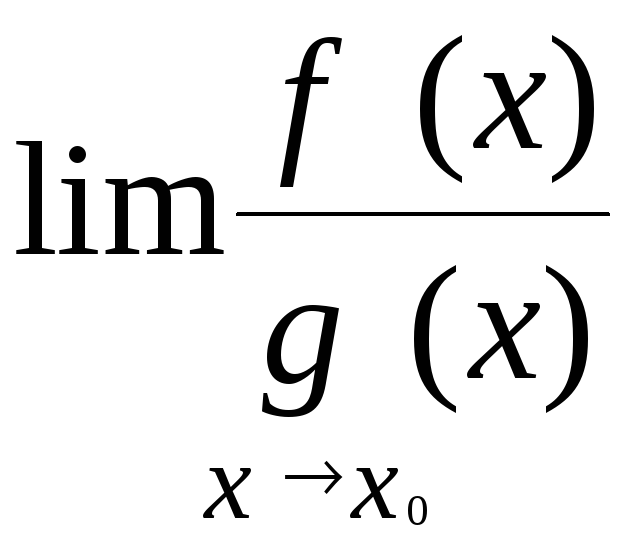 =
=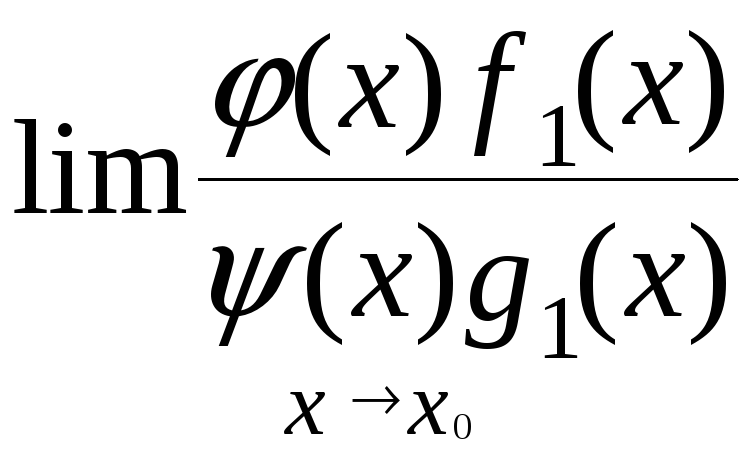 =
=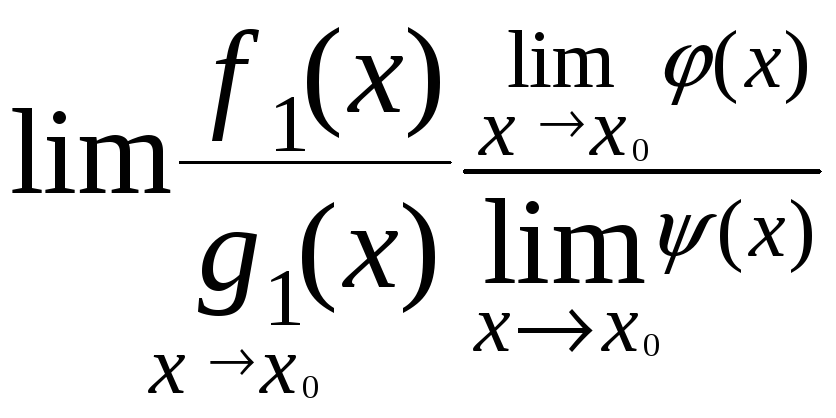 =
=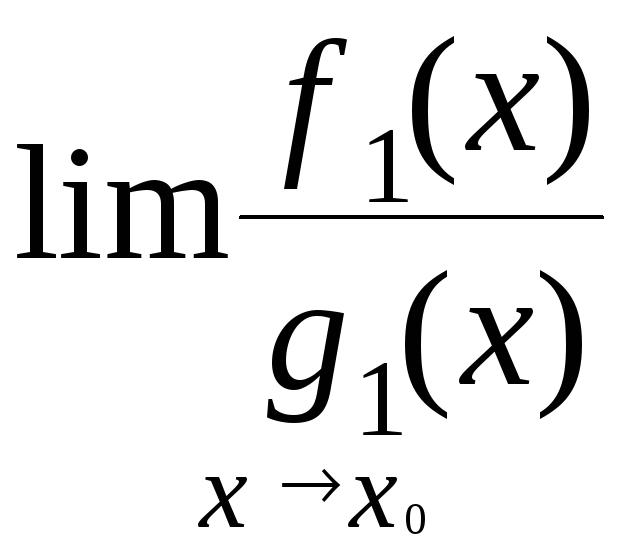
либо оба предела не существуют.
Пример 2. Вычислить предел
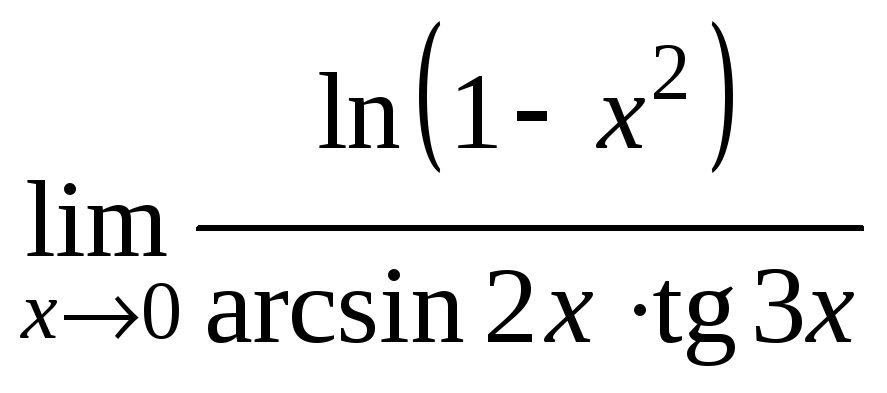 .
.
Решение. Поскольку
ln(1-x2)~-x2, arcsin2x~2x, tg3x~3x при
![]() ,
то
,
то
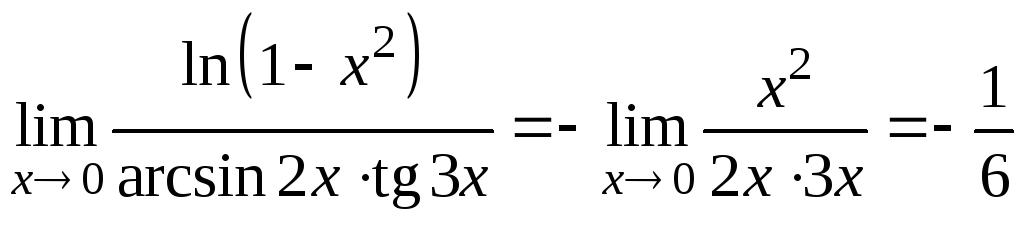 .
.
Пример
2.16. Показать, что бесконечно малые
величины
![]() и
и
![]() при
при
![]() являются эквивалентными.
являются эквивалентными.
Решение:
Рассмотрим
![]()
Пример
2.17. Показать, что бесконечно малые
величины
![]() и
и
![]() при
при
![]() являются эквивалентными.
являются эквивалентными.
Решение:
Рассмотрим
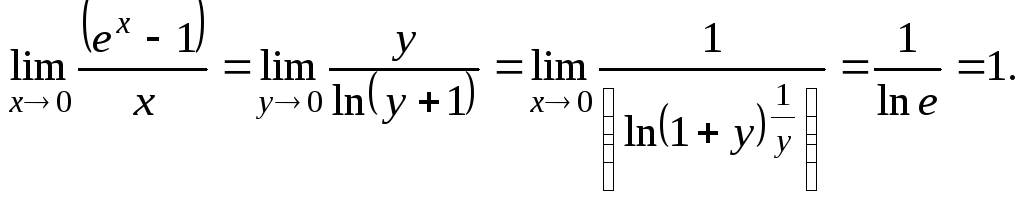
Бесконечно
малая величина
![]() является бесконечно малой величиной
более высокого порядка малости по
сравнению с бесконечно малой величиной
является бесконечно малой величиной
более высокого порядка малости по
сравнению с бесконечно малой величиной![]() ,
если
,
если
![]() .
.
При вычислении пределов бесконечно малые величины могут заменяться эквивалентными.
Ниже приведены важнейшие эквивалентности, которые используются при вычислении пределов:
-
sin x ~ x при x→0;
-
tg x ~ x при x→0;
-
arcsin x ~ x при x→0;
-
arctg x ~ x при x→0;
-
1 – cos x ~
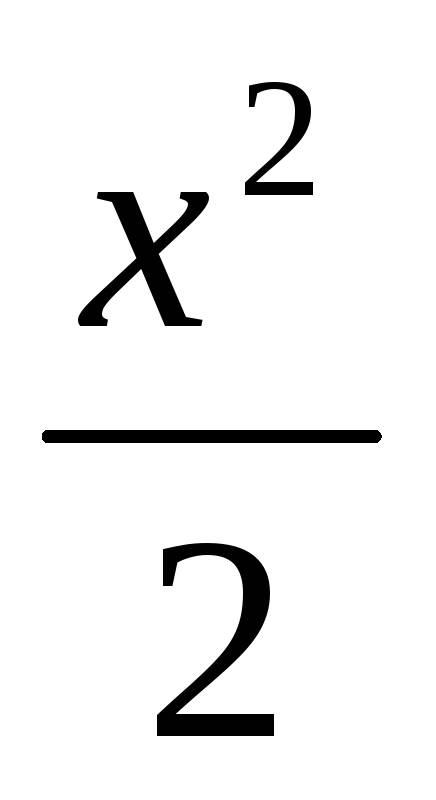 при
x→0;
при
x→0; -
ex – 1 ~ x при x→0;
-
ax – 1~ x·lna при x→0;
-
ln(1+x) ~ x при x→0;
-
loga(1+x) ~ x·logae при x→0;
-
(1+x)k -1~k· x, k >0 при x→0; в частности,
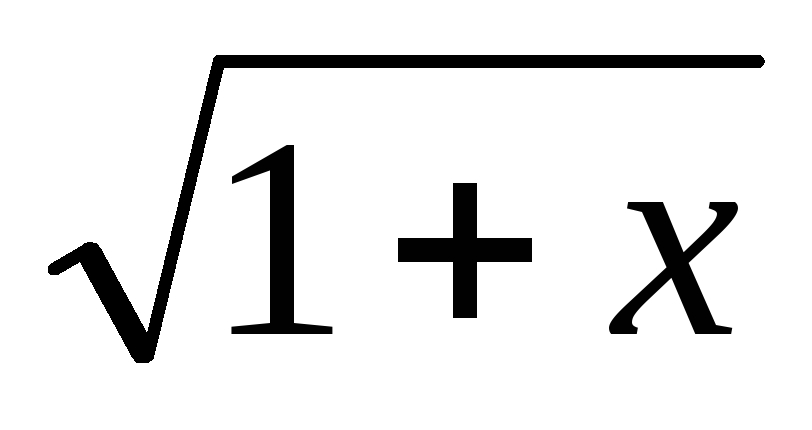 -1
x
~
-1
x
~