
- •Лекция №7 предел функции
- •4.1. Определения предела функции в точке.Теорема об эквивалентности определений. Односторонние пределы.
- •4.2. Бесконечно малые функции, их свойства. Бесконечно большие функции
- •4.3. Основные теоремы о пределах
- •4.4. Признаки существования пределов
- •Раскрытие некоторых неопределенностей
- •4.5. Критерий Коши
- •4.6 Сравнение бесконечно малых функций
- •Вычислить пределы функций.
- •4. Задачи Группа а
- •Группа б
- •Группа в
4.4. Признаки существования пределов
Теорема
1. Если функция
![]() – неубывающая и ограничена сверху, то
существует ее предел
– неубывающая и ограничена сверху, то
существует ее предел
![]() .
Если функция
.
Если функция
![]() – невозрастающая и ограничена снизу,
то существует ее предел
– невозрастающая и ограничена снизу,
то существует ее предел
![]() .
.
На основании
данного признака доказывается
существование второго
замечательного предела
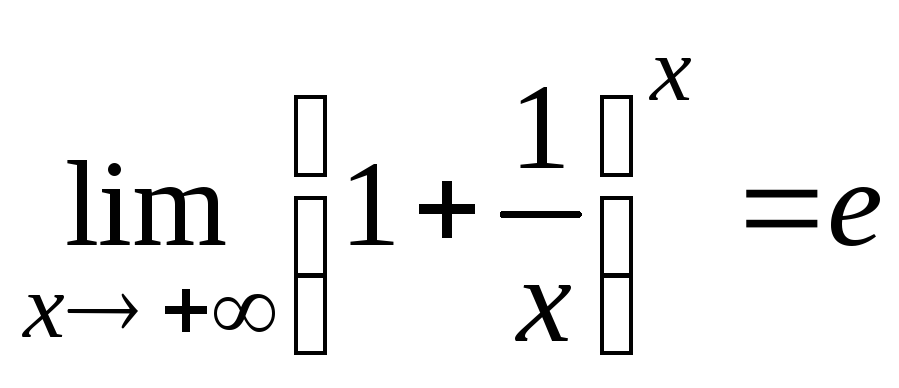 ,
где
,
где
![]() -
иррациональное число
-
иррациональное число
![]() .
.
Если
в равенстве положить 1/x
=a, то
при
![]() имеем
имеем
![]() и получаем
и получаем
![]() используем при раскрытии,
неопределенность вида
используем при раскрытии,
неопределенность вида
![]() .
.
При решении конкретных задач на пределы могут быть полезны модифицированные варианты записи второго замечательного предела:
![]() ,
,
![]() ,
,
где
![]() является бесконечно большой величиной,
а
является бесконечно большой величиной,
а
![]() - бесконечно малой величиной при
- бесконечно малой величиной при
![]() ,
или при
,
или при![]() .
.
Пример 1.
![]()
![]() =
=![]()
![]()
![]() =
=
=
![]()
![]()
![]()
![]() =
е×1=е.
=
е×1=е.
Пример 2.
![]()
![]() =
=![]()
![]()
![]()
![]() =
=
=![]()
![]()
![]()
![]()
![]()
![]() =
е× е×
е =
=
е× е×
е =![]()
![]()
![]()
Пример 2.
![]()
![]() =
=![]()
![]() =
=![]()
![]()
=![]()
![]() =
=![]()
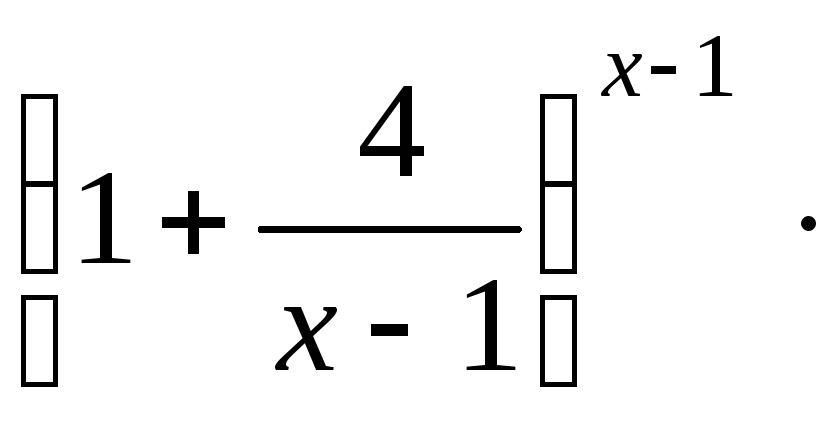
![]()
![]() =
=
=![]()
![]() =
=![]()
Пример
3. Вычислить предел
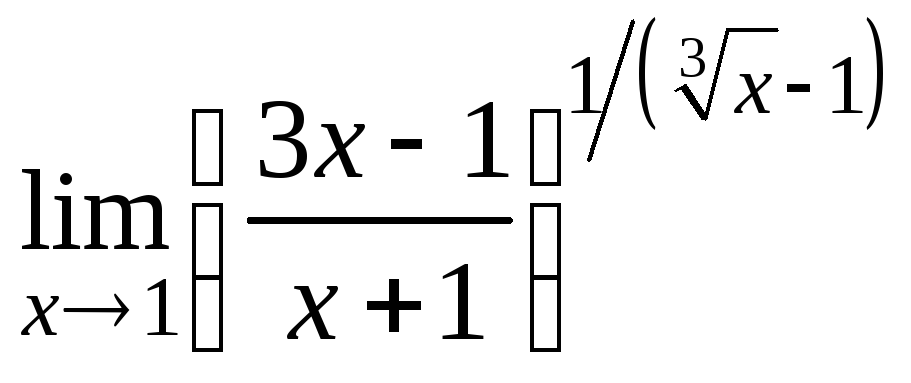 .
.
Решение.
Этот предел
является неопределенностью
вида
![]() .
Сделаем замену
.
Сделаем замену
![]() .
Тогда
.
Тогда
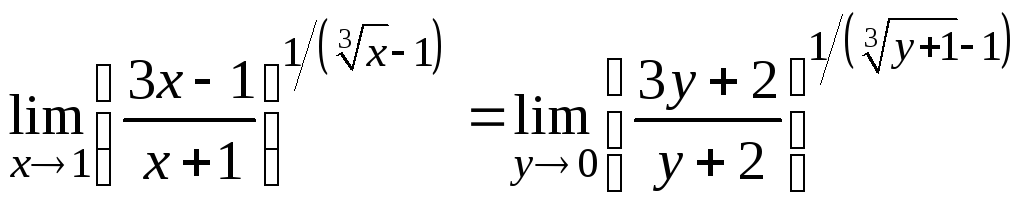 .
.
Приводим
дробь к виду
![]() ,
где
,
где
![]() – бесконечно малая функция, и умножаем
и делим степень на
– бесконечно малая функция, и умножаем
и делим степень на
![]() .
Получаем
.
Получаем
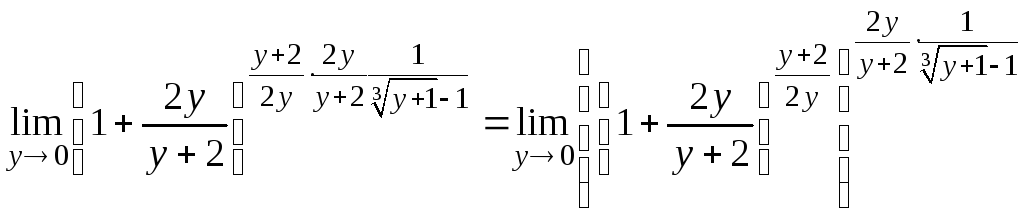 .
.
Применив
второй замечательный предел, преобразуем
данный предел к виду
![]() .
Полученный предел является неопределенностью
вида
.
Полученный предел является неопределенностью
вида
![]() ,
поэтому умножаем числитель и знаменатель
на выражение, дополняющее знаменатель
второй дроби до разности кубов. Получаем
,
поэтому умножаем числитель и знаменатель
на выражение, дополняющее знаменатель
второй дроби до разности кубов. Получаем
![]() .
.
Теорема
2 (о пределе промежуточной переменной).
Пусть функции
![]() ,
,
![]() ,
,
![]() определены в некоторой окрестности
точки
определены в некоторой окрестности
точки
![]() ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
![]() и удовлетворяют неравенствам
и удовлетворяют неравенствам
![]() .
Если при этом
.
Если при этом
![]() ,
тогда и
,
тогда и
![]() .
.
С
помощью теоремы о пределе промежуточной
переменной доказывается существование
первого замечательного
предела
![]() .
.
Раскрытие некоторых неопределенностей
Рассмотрим
предел функции![]() (или
при
(или
при![]() ),
который при непосредственной подстановке
),
который при непосредственной подстановке
![]() =
=
![]() приходит к одному из случаев
неопределенности. Укажем приемы для
решения таких примеров, приемы «раскрытия
неопределенности».
приходит к одному из случаев
неопределенности. Укажем приемы для
решения таких примеров, приемы «раскрытия
неопределенности».
1.Рассмотрим
предел отношения многочленов при
![]()
![]() ,
,
где
![]() ,
,
![]()
![]() .
Для раскрытия получающейся неопределенности
.
Для раскрытия получающейся неопределенности
![]() необходимо вынести
необходимо вынести
![]() в старшей степени в числителе и знаменателе
в старшей степени в числителе и знаменателе
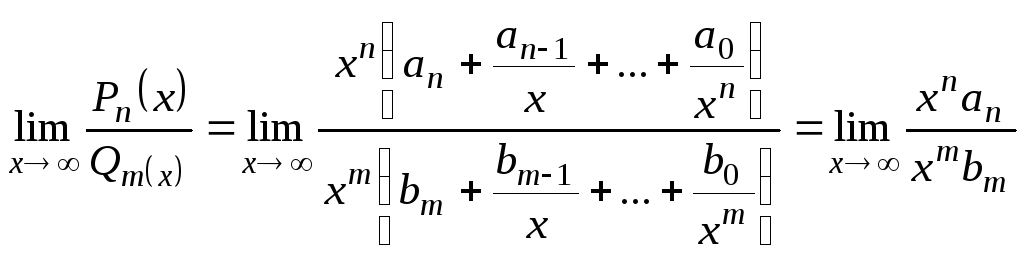 .
.
Если
![]() ,
то предел равен отношению коэффициентов
при старших степенях
,
то предел равен отношению коэффициентов
при старших степенях
![]() .
Если же
.
Если же
![]() >
>![]() ,
то
,
то
![]()
![]() =0.
=0.
В
случае
![]() >
>![]()
![]() =
=![]() ,
,
где знак бесконечности
определяется знаком коэффициента![]() .
.
Пример 6.
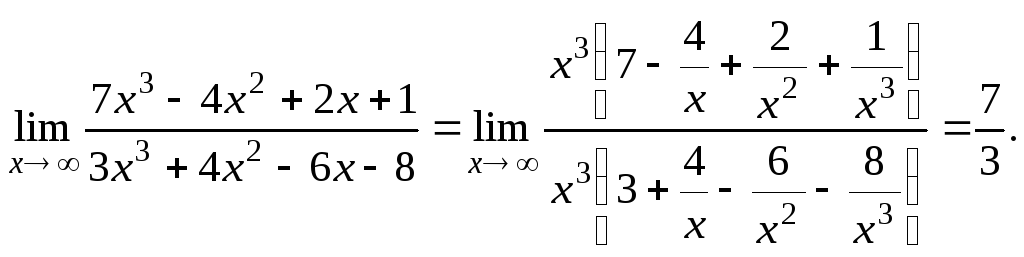
Здесь
было использовано, что при
![]() величины
величины
![]() стремятся к нулю.
стремятся к нулю.
2.
Если в пределе многочлены в числителе
и знаменателе стремятся к нулю, то
получается неопределенность вида
![]() ,
для раскрытия которой надо разложить
числитель и знаменатель на множители
и сократить одинаковые бесконечно малые
величины.
,
для раскрытия которой надо разложить
числитель и знаменатель на множители
и сократить одинаковые бесконечно малые
величины.
Пусть
![]() является действительным корнем кратности
является действительным корнем кратности
![]() многочлена, стоящего в числителе, т.е.
многочлена, стоящего в числителе, т.е.
![]() ,
где
,
где
![]() .
.
Кроме
того,
![]() является
действительным корнем кратности
является
действительным корнем кратности
![]() многочлена знаменателя, т.е.
многочлена знаменателя, т.е.
![]() ,
где
,
где
![]() .
.
Если
![]() =
=![]() ,
то
,
то
![]()
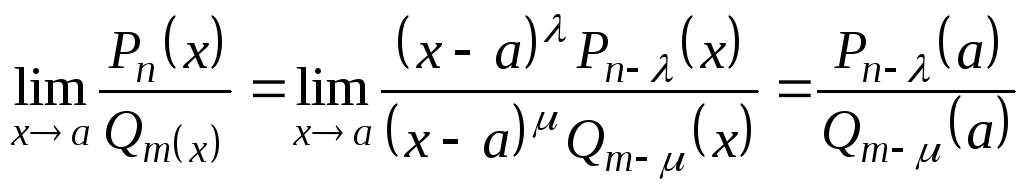 .
.
Если
![]() >
>![]() ,
то
,
то
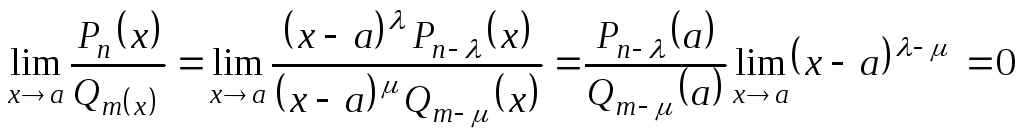 .
.
Если
![]() <
<![]() ,
то
,
то
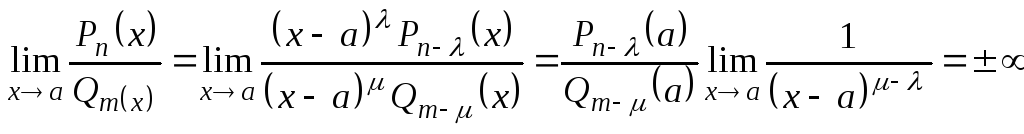 .
.
Пример 7.
![]() .
.
Пример 8.
![]() .
.
3.
Если дробь является иррациональной,
т.е. в числителе или знаменателе есть
корни, то для раскрытия неопределенности
вида
![]() необходимо выделять в качестве множителей
бесконечно малые величины, не содержащие
радикалов, посредством умножения
числителя и знаменателя на сопряженное
выражение.
необходимо выделять в качестве множителей
бесконечно малые величины, не содержащие
радикалов, посредством умножения
числителя и знаменателя на сопряженное
выражение.
Пример 9.
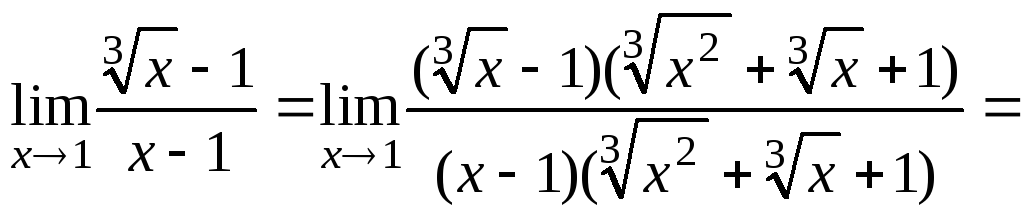
![]()
Пример 10.
![]()
![]() .
.
При
раскрытии неопределенности вида
![]() для представления бесконечно малых
величин в удобном виде, не содержащем
иррациональности, необходимо умножить
и разделить на сопряженное выражение.
для представления бесконечно малых
величин в удобном виде, не содержащем
иррациональности, необходимо умножить
и разделить на сопряженное выражение.
Пример 11.
![]()

![]() .
.
Раскрытие
другого варианта неопределенности вида
![]() требует приведения к общему знаменателю.
В результате преобразований получим
уже рассмотренный случай неопределенности
требует приведения к общему знаменателю.
В результате преобразований получим
уже рассмотренный случай неопределенности
![]() .
.
Пример 12.
![]()
![]()
![]()
