
- •Лекция №7 предел функции
- •4.1. Определения предела функции в точке.Теорема об эквивалентности определений. Односторонние пределы.
- •4.2. Бесконечно малые функции, их свойства. Бесконечно большие функции
- •4.3. Основные теоремы о пределах
- •4.4. Признаки существования пределов
- •Раскрытие некоторых неопределенностей
- •4.5. Критерий Коши
- •4.6 Сравнение бесконечно малых функций
- •Вычислить пределы функций.
- •4. Задачи Группа а
- •Группа б
- •Группа в
Лекция №7 предел функции
4.1. Определения предела функции в точке.Теорема об эквивалентности определений. Односторонние пределы.
Впервые определение предела функции было дано О. Коши в 1821 г.
Пусть
функция
![]() определена на некотором множестве
определена на некотором множестве
![]() .
Рассмотрим последовательность точек
.
Рассмотрим последовательность точек
![]() ,
сходящуюся к точке
,
сходящуюся к точке
![]() ,
при этом
,
при этом
![]() может и не принадлежать множеству
может и не принадлежать множеству
![]() .
Соответствующие значения функции в
точках этой последовательности также
образуют числовую последовательность
.
Соответствующие значения функции в
точках этой последовательности также
образуют числовую последовательность
![]() .
.
Определение
1 (по Гейне). Число
![]() называется пределом
функции
называется пределом
функции
![]() в точке
в точке
![]() (при
(при
![]() ),
пишут
),
пишут
![]() ,
если для любой сходящейся к
,
если для любой сходящейся к
![]() последовательности значений аргумента
последовательности значений аргумента
![]() ,
отличных от
,
отличных от
![]() ,
соответствующая последовательность
значений функции
,
соответствующая последовательность
значений функции
![]() сходится к числу
сходится к числу
![]() .
.
Функция
![]() может иметь в точке только один предел,
так как последовательность
может иметь в точке только один предел,
так как последовательность
![]() имеет только один предел.
имеет только один предел.
Определение
2 (по Коши). Число
![]() называется пределом
функции
называется пределом
функции
![]() в точке
в точке
![]() (при
(при
![]() ),
пишут
),
пишут
![]() ,
если для любого числа
,
если для любого числа
![]() существует такое число
существует такое число
![]() ,
что для всех
,
что для всех
![]() (
(![]() ),
удовлетворяющих неравенству
),
удовлетворяющих неравенству
![]() ,
выполняется
,
выполняется
![]() .
.
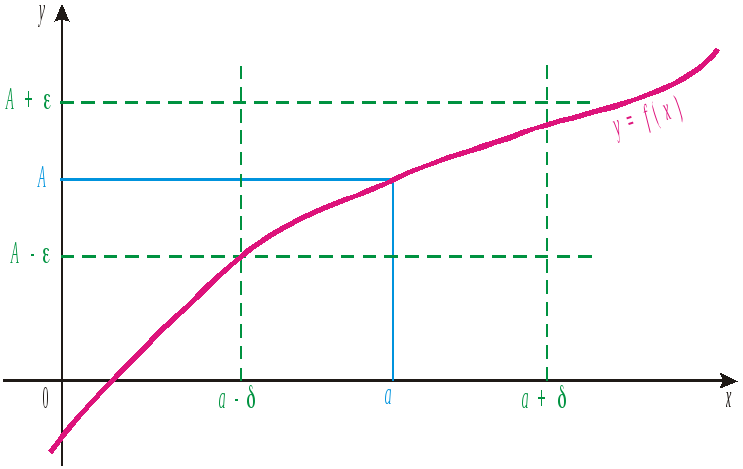
Рис. 1
Определение
3 (геометрическое определение предела
функции). Число
![]() называется пределом функции
называется пределом функции
![]() ,
если для любой
,
если для любой
![]() окрестности
точки
окрестности
точки
![]() найдется такая
найдется такая
![]() окрестность
точки
окрестность
точки
![]() ,
что для всех
,
что для всех
![]() из этой
из этой
![]() окрестности
соответствующие значения функции лежат
в
окрестности
соответствующие значения функции лежат
в
![]() окрестности
точки
окрестности
точки
![]() ,
т.е. точки графика функции
,
т.е. точки графика функции
![]() лежат внутри полосы шириной
лежат внутри полосы шириной
![]() ,
ограниченной прямыми
,
ограниченной прямыми
![]() ,
,
![]() .
Очевидно, что величина
.
Очевидно, что величина
![]() зависит от выбора
зависит от выбора
![]() (рис. 1).
(рис. 1).
Пример
1. Доказать, что
![]() .
.
Решение.
Воспользуемся неравенством
![]()
![]() .
Зададим произвольное
.
Зададим произвольное
![]() и положим
и положим
![]() .
Тогда, если
.
Тогда, если
![]() ,
то
,
то
![]() .
Это и означает (согласно определению
предела функции по Коши), что
.
Это и означает (согласно определению
предела функции по Коши), что
![]() .
.
Теорема 1. Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство.
Пусть b является
пределом функции
![]() в точке а
по Коши. Докажем, что это же число является
пределом функции
в точке а
по Коши. Докажем, что это же число является
пределом функции
![]() в точке а
по Гейне. Пусть
в точке а
по Гейне. Пусть
![]() – любая сходящаяся к а
последовательность значений аргумента,
все элементы которой отличны от а.
Требуется доказать, что соответствующая
последовательность значений функции
– любая сходящаяся к а
последовательность значений аргумента,
все элементы которой отличны от а.
Требуется доказать, что соответствующая
последовательность значений функции
![]() сходится к b.
сходится к b.
Фиксируем
произвольное положительное число ε
и по нему положительное число δ,
которое в силу определения предела
функции по Коши гарантирует справедливость
неравенства
![]() для
всех значений х,
для которых 0<|x–a|<δ.
В силу сходимости последовательности
для
всех значений х,
для которых 0<|x–a|<δ.
В силу сходимости последовательности
![]() к а для
указанного числа δ
найдётся такой номер N,
что при всех n
к а для
указанного числа δ
найдётся такой номер N,
что при всех n![]() N
справедливо неравенство
N
справедливо неравенство
![]() .
Поскольку
.
Поскольку
![]() для всех номеров n, то
при всех
для всех номеров n, то
при всех
![]() справедливы неравенства 0<
справедливы неравенства 0<![]() и, значит, в силу определения предела
функции по Коши
и, значит, в силу определения предела
функции по Коши
![]() ,
но это и означает сходимость
последовательности
,
но это и означает сходимость
последовательности
![]() к числу b.
к числу b.
Пусть
теперь число b является
пределом функции
![]() в точке а
по Гейне. Докажем, что это же число
является пределом функции
в точке а
по Гейне. Докажем, что это же число
является пределом функции
![]() в точке а
по Коши. Предположим, что это не так.
Тогда для некоторого положительного
числа ε и для любого
сколь угодно малого положительного
числа δ найдётся хотя
бы одно значение аргумента х,
такое, что
в точке а
по Коши. Предположим, что это не так.
Тогда для некоторого положительного
числа ε и для любого
сколь угодно малого положительного
числа δ найдётся хотя
бы одно значение аргумента х,
такое, что
![]() ,
но
,
но
![]() .
Таким образом, мы можем взять
последовательность
.
Таким образом, мы можем взять
последовательность
![]() с натуральными n и
утверждать, что для каждого ее элемента
с натуральными n и
утверждать, что для каждого ее элемента
![]() найдется хотя бы одно значение аргумента
xn такое,
что
найдется хотя бы одно значение аргумента
xn такое,
что
![]() ,
но
,
но
![]() .
Левое из неравенств означает, что
последовательность {xn}
сходится к числу а
и состоит из чисел, отличных от а.
Но в таком случае согласно определению
предела по Гейне соответствующая
последовательность значений функции
.
Левое из неравенств означает, что
последовательность {xn}
сходится к числу а
и состоит из чисел, отличных от а.
Но в таком случае согласно определению
предела по Гейне соответствующая
последовательность значений функции
![]() обязана сходится к b,
а этому противоречит правое из неравенств,
справедливое для всех номеров n.
Полученное противоречие доказывает
теорему.
обязана сходится к b,
а этому противоречит правое из неравенств,
справедливое для всех номеров n.
Полученное противоречие доказывает
теорему.
Пример
2. Доказать, что функция
![]() не имеет предела при
не имеет предела при
![]() .
.
Решение.
Докажем, что эта функция
не удовлетворяет определению предела
функции при
![]() по Гейне. Для этого укажем такую бесконечно
большую последовательность
по Гейне. Для этого укажем такую бесконечно
большую последовательность
![]() ,
что последовательность
,
что последовательность
![]() расходится. Положим
расходится. Положим
![]() .
Тогда
.
Тогда
![]() ,
а последовательность
,
а последовательность
![]() расходится. Отсюда следует, что функция
расходится. Отсюда следует, что функция
![]() не имеет предела при
не имеет предела при
![]() .
.
В
определении предела функции считается,
что
![]() стремится к
стремится к
![]() любым способом, оставаясь меньше или
больше, чем
любым способом, оставаясь меньше или
больше, чем
![]() .
Если способ приближения аргумента
.
Если способ приближения аргумента
![]() к
к
![]() существенно влияет на значение предела,
то рассматриваются односторонние
пределы.
существенно влияет на значение предела,
то рассматриваются односторонние
пределы.
Определение
4. Число
![]() называется правым
(левым) пределом функции
называется правым
(левым) пределом функции
![]() в точке
в точке
![]() при
при
![]() ,
пишут
,
пишут
![]() (
(![]() ),
если для любого числа
),
если для любого числа
![]() существует такое число
существует такое число
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() (
(![]() ),
выполняется неравенство
),
выполняется неравенство
![]() .
.
Теорема
2. Для того, чтобы функция
![]() имела в точке
имела в точке
![]() предел, необходимо и достаточно, чтобы
в этой точке существовали левый и правый
пределы и чтобы они были равны. В этом
случае предел функции равен односторонним
пределам
предел, необходимо и достаточно, чтобы
в этой точке существовали левый и правый
пределы и чтобы они были равны. В этом
случае предел функции равен односторонним
пределам
![]() .
.
Доказательство.
В самом деле, пусть
![]() .
Тогда, согласно определению предела
функции в точке a,
это означает, что для любого числа ε>0
существует такое число δ>0,
что для всех точек x,
удовлетворяющих условию
.
Тогда, согласно определению предела
функции в точке a,
это означает, что для любого числа ε>0
существует такое число δ>0,
что для всех точек x,
удовлетворяющих условию
![]() ,
,
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
Тем самым, как для точек x,
таких, что
.
Тем самым, как для точек x,
таких, что
![]() ,
так и для таких, что
,
так и для таких, что
![]() ,
справедливо неравенство
,
справедливо неравенство
![]() .
А это, согласно определению и означает,
что число А
является как пределом функции справа,
так и пределом функции слева:
.
А это, согласно определению и означает,
что число А
является как пределом функции справа,
так и пределом функции слева:
![]() .
.
Обратно,
пусть существуют оба предела и они
равны![]() .
Согласно определению для всякого ε>0
существуют такие
.
Согласно определению для всякого ε>0
существуют такие
![]() и
и
![]() ,
что для всех х,
удовлетворяющих условию
,
что для всех х,
удовлетворяющих условию
![]() и для всех х,
удовлетворяющих условию
и для всех х,
удовлетворяющих условию
![]() справедливо неравенство
справедливо неравенство![]() .
Если обозначить через δ
наибольшее из чисел δ1
и δ2,
то очевидно, что для всех х,
удовлетворяющих условию
.
Если обозначить через δ
наибольшее из чисел δ1
и δ2,
то очевидно, что для всех х,
удовлетворяющих условию
![]() ,
,
![]() ,
будет справедливо неравенство
,
будет справедливо неравенство
![]() .
Это и означает, что
.
Это и означает, что
![]() .
.
Пример 3. Пусть
![]()
и не
определена при
![]() .
Существует ли
.
Существует ли
![]() ?
?
Решение.
Вычислим в точке
![]() односторонние пределы функции
односторонние пределы функции
![]() ;
;
![]() .
.
Отсюда по
теореме 2 следует, что
![]() существует и равен нулю.
существует и равен нулю.
Дадим определение предела функции при стремлении аргумента к бесконечности.
Определение
5.
Число
![]() называется пределом
функции
называется пределом
функции
![]() при
при
![]() ,
пишут
,
пишут
![]() ,
если для любого числа
,
если для любого числа
![]() существует такое число N,
что для всех
существует такое число N,
что для всех
![]() (
(![]() ),
удовлетворяющих неравенству
),
удовлетворяющих неравенству
![]() ,
выполняется
,
выполняется
![]() .
.
Определение
предела
![]() функции
функции
![]() при
при
![]() графически иллюстрируется следующим
образом:
графически иллюстрируется следующим
образом:
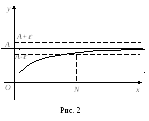
Для
любой сколь угодно малой -окрестности
около ординаты
![]() найдется такое значение
найдется такое значение
![]() ,
что для всех
,
что для всех
![]()
![]() график функции не будет выходить за
пределы полосы шириной 2.
график функции не будет выходить за
пределы полосы шириной 2.
