Лекция №9

5. Первый и второй замечательные пределы

Теорема 1. – первый замечательный предел. Читается: предел

отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю.

Д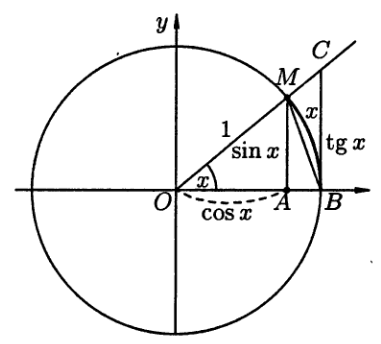оказательство. Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. (см.рис.1). Пусть 0 < x <. На рисунке |AM|=sinx, дуга МВ численно равна центральному углу x, |BC| = tgx. Очевидно, имеем S_ΔМОВ < S_{сектора МОВ} < S_ΔCОВ. На основании соответствующих формул геометрии получаем Разделим неравенства на получим

или Так как и ,

то по признаку (о пределе промежуточной функции) существования пределов

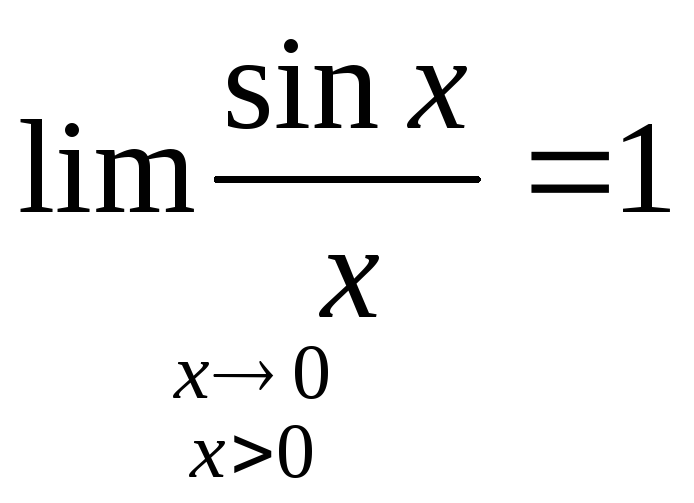(1)

Пусть теперь x < 0. Имеем где –x >0

Поэтому 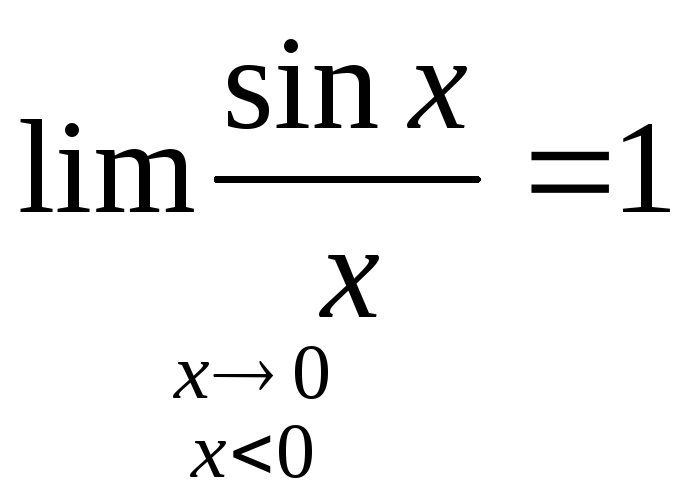(2)

Рис.1. Из равенств (1) и (2) вытекает равенство

Следствия.

1. .

2. .

3. .

Пример 1.

Пример 2.

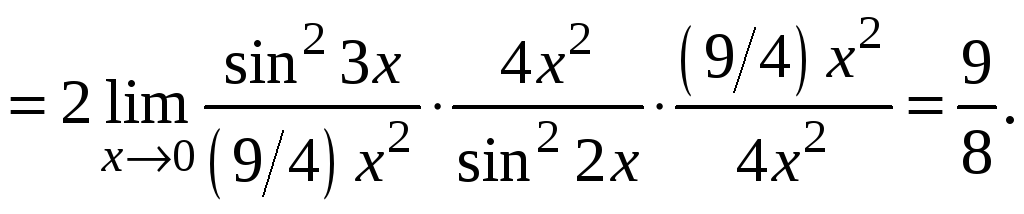
Теорема 2. 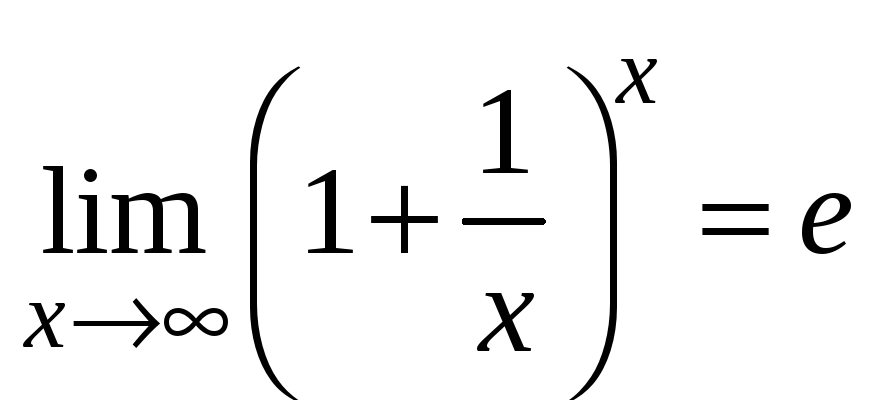– второй замечательный предел.

Доказательство. Рассмотрим переменную величину . Так как для любого действительного х, справедливо неравенство , то, очевидно,

.

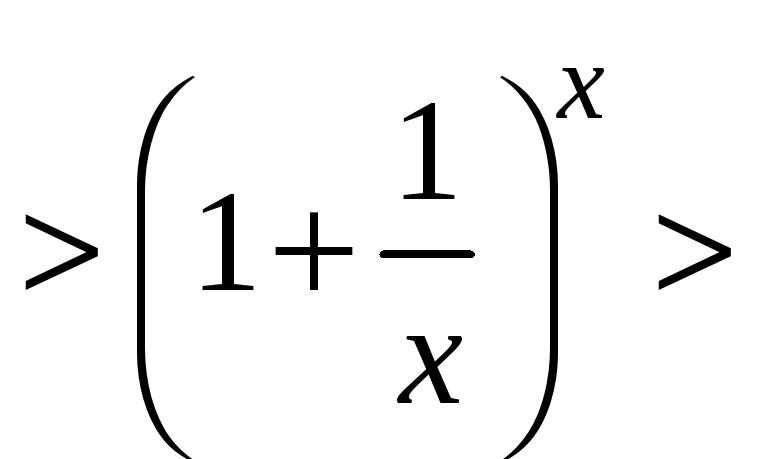
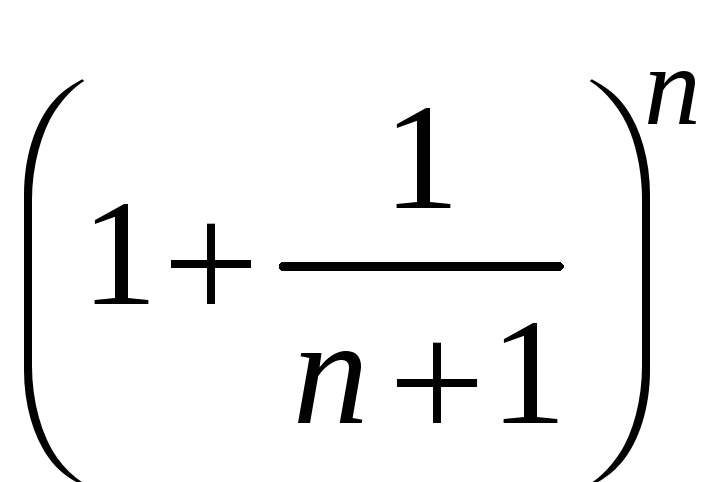Легко показать (п. 2.5), что

, ,

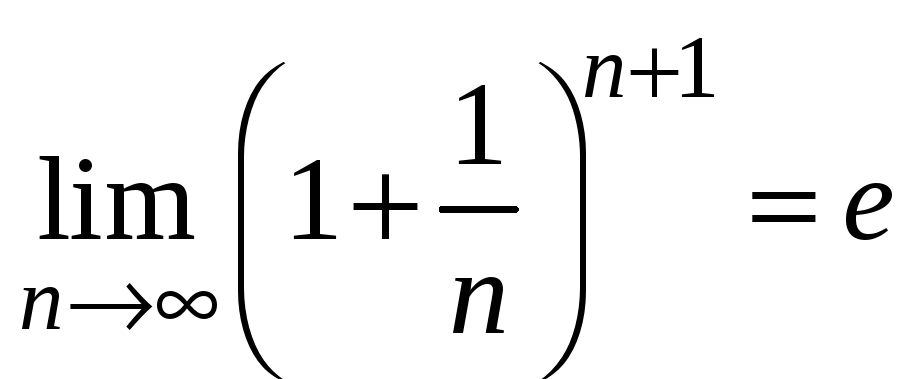_{а, значит, по теореме 3 (п. 4.2) о промежуточной переменной}

,

где – иррациональное число .

Следствия.

1. .

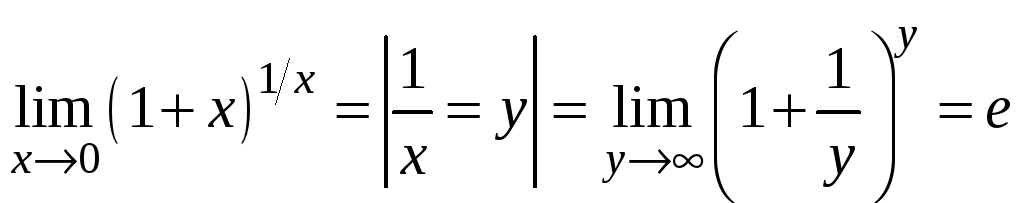2.

.

3. – следует из 2.

4.

– следует из 3.

5. 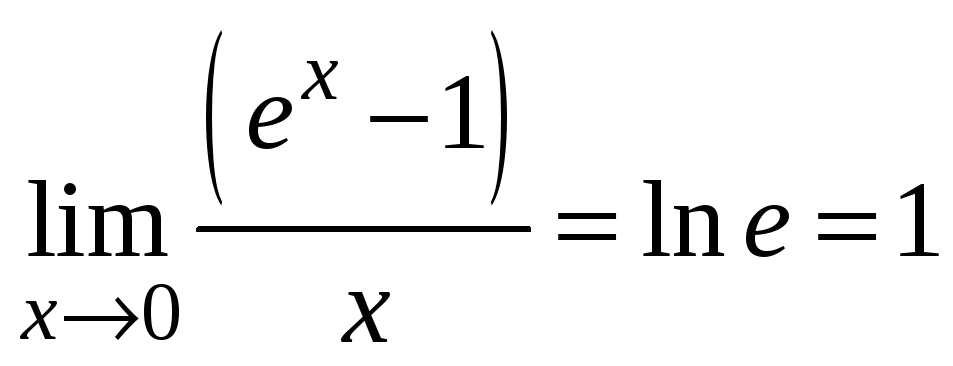– следует из 4.

Пример 3. ==

==.

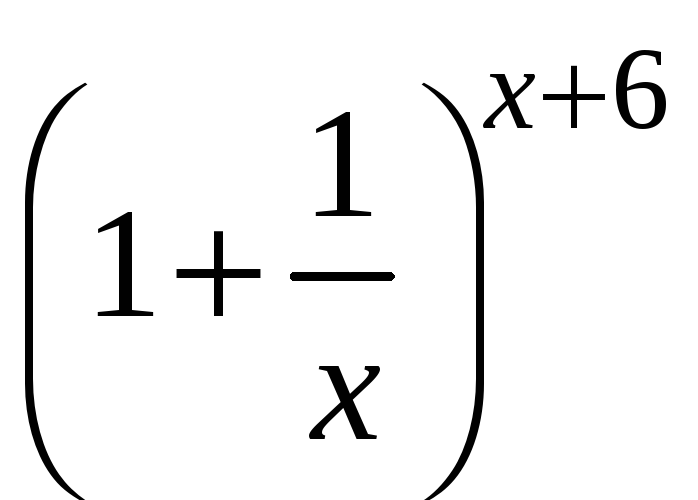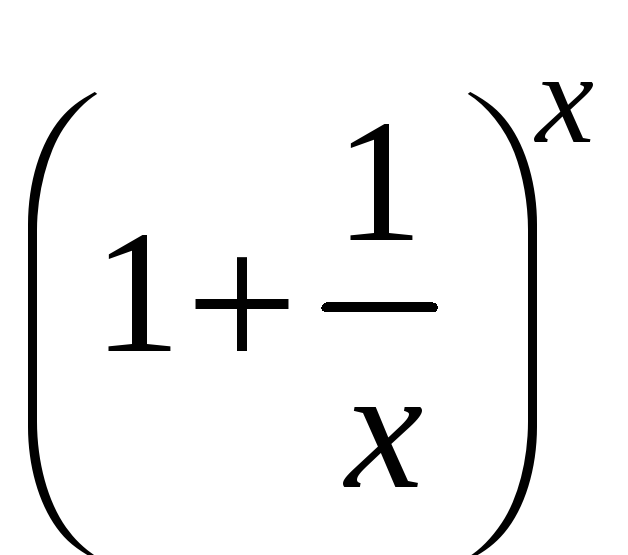
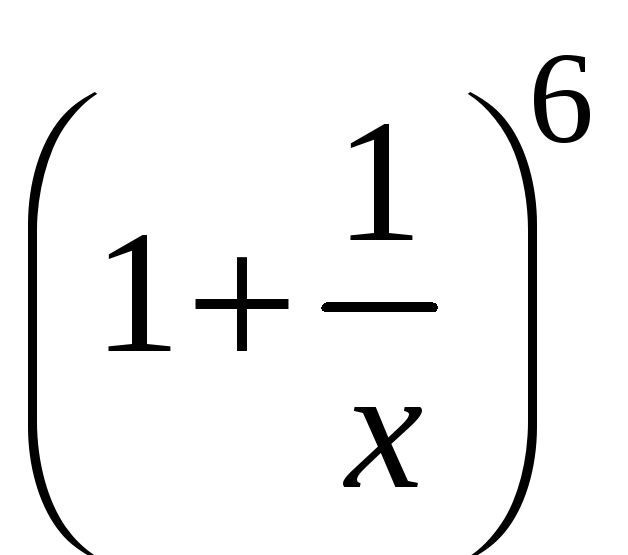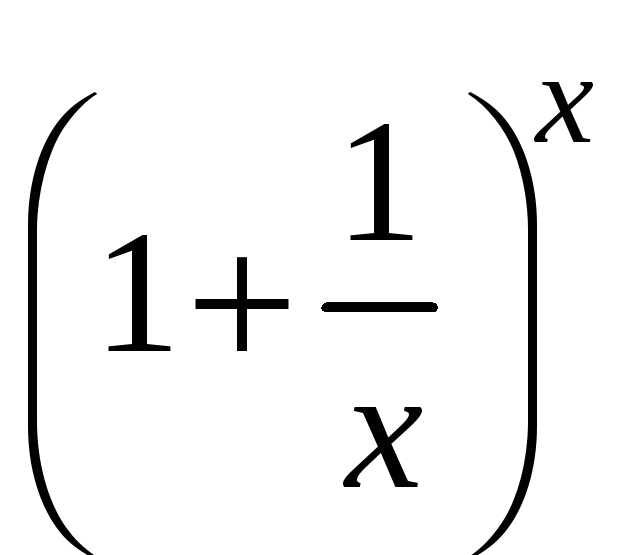
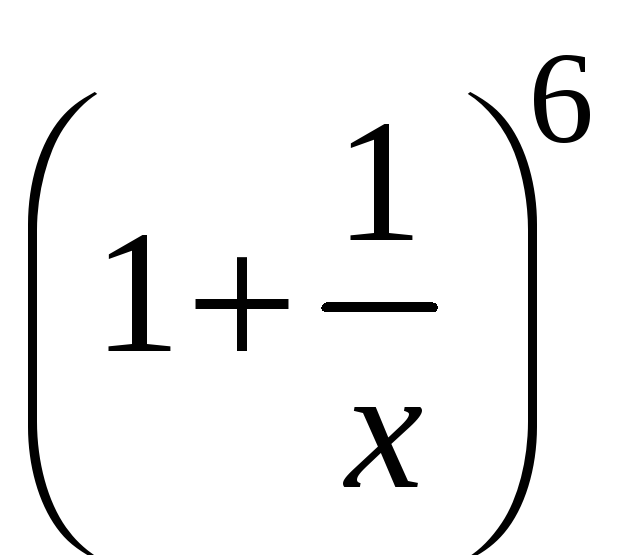Пример 4. ==

===

==

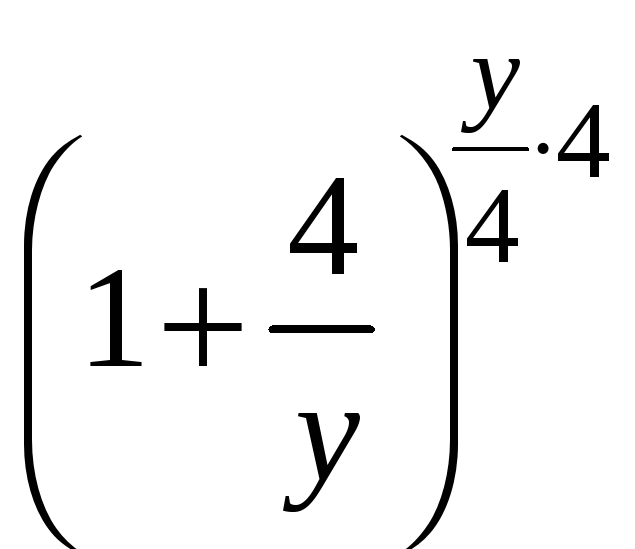
5.6. Свойства функций, непрерывных на отрезке. Теоремы Вейерштрасса и Больцано-Коши

Определение. Функция называется непрерывной на отрезке , если она непрерывна в каждой внутренней точке отрезка, в точке справа, а в точке слева.

Теорема 1 (первая теорема Вейерштрасса). Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

Лемма. Функция , непрерывная в точке , ограничена в некоторой ее окрестности.

Доказательство леммы. Пусть ; тогда согласно второму определению непрерывности функции в точке для данного существует такое, что для всех выполняется неравенство . Используя это неравенство, получаем , т.е. , где . Отсюда заключаем, что функция ограничена в -окрестности точки .

Доказательство теоремы. Предположим обратное, т.е. допустим, что функция неограниченна на отрезке . Разделим отрезок пополам, тогда, по крайней мере, на одном из двух полученных отрезков функция неограничена (в противном случае она была бы ограничена на ). Обозначим этот отрезок через . Разделим пополам и обозначим через тот отрезок, на котором функция не ограничена, и т.д. Продолжая этот процесс неограниченно, получаем последовательность вложенных отрезков

,

на каждом из которых не ограничена, причем при . По лемме о вложенных отрезках существует точка , принадлежащая всем отрезкам. Функция по условию определена и непрерывна в точке , следовательно, согласно доказанной лемме в некоторой окрестности точки она ограничена. При достаточно большом в эту окрестность попадет отрезок , на котором функция также ограничена. Но это противоречит тому, что не ограничена на каждом из вложенных отрезков. Полученное противоречие доказывает теорему.

Для интервала теорема 1 не имеет места. Так, например, функция непрерывна на , но не ограничена на этом интервале.

Разрывная функция, определенная в любой точке отрезка, может не быть ограниченной на этом отрезке, например,

.

Теорема 2 (вторая теорема Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений: , (рис. 52).

Доказательство. Так как функция непрерывна на отрезке , то по теореме 1 она ограничена на этом отрезке. Следовательно, существуют точная верхняя и точная нижняя грани функции на отрезке . Покажем, что функция достигает , т.е. существует такая точка , что . Будем рассуждать от противного. Пусть функция не принимает ни в одной точке значения, равного . Тогда для всех справедливо неравенство . Рассмотрим на вспомогательную, всюду положительную функцию . Функция непрерывна как частное двух непрерывных функций. Следовательно, функция ограничена, т.е. найдется положительное число такое, что для всех , откуда . Таким образом, число , меньшее , является верхней гранью на отрезке . Но это противоречит тому, что число является точной верхней, т.е. наименьшей верхней гранью функции на отрезке . Это противоречие и доказывает, что существует точка , в которой .

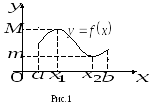Аналогично доказывается, что функция достигает на своей точной нижней грани .

Изображенная на рис. 52 функция непрерывна на отрезке , принимает наибольшее значение в точке , а наименьшее – в точке . Для любого имеет место неравенство .

Разрывная функция, определенная в любой точке отрезка, может не быть ограниченной на этом отрезке, например,

Теорема 2 не решает вопрос о числе точек, в которых непрерывная на отрезке функция имеет наибольшее (наименьшее) значение, она утверждает о существовании по крайней мере одной такой точки. Так, функция на отрезке имеет и и достигает их соответственно в точках , и , .

Если функция непрерывна на интервале или разрывна на отрезке, то теорема 2 не верна. Приведите примеры.

Рассмотрим теорему о прохождении непрерывной функции через нулевое значение при смене знаков.

Теорема 3 (первая теорема Больцано-Коши). Если функция непрерывна на отрезке и на концах его принимает значения разных знаков, то найдется хотя бы одна точка , в которой обращается в нуль: .

Доказательство. Пусть для определенности и (рис. 53). Разделим отрезок пополам. Если значение функции в середине отрезка равно нулю, то теорема доказана. В противном случае выберем тот из двух полученных отрезков, на концах которого функция имеет значения разных знаков, и обозначим его . Разделим отрезок пополам. Если значение функции в середине отрезка равно нулю, то теорема доказана. В противном случае выберем тот из двух полученных отрезков, на концах которого функция имеет значения разных знаков, и обозначим его . Если продолжать этот процесс неограниченно, то либо на каком-то -м шаге значение функции в середине отрезка окажется равным нулю и тогда теорема доказана, либо получим последовательность вложенных отрезков , причем при и на концах каждого отрезка функция имеет значения разных знаков. По лемме о вложенных отрезках существует точка , принадлежащая всем отрезкам. Докажем, что . Действительно, если допустить, что , то по теореме об устойчивости знака непрерывной функции существует окрестность точки , в которой . В эту окрестность при достаточно большом попадет отрезок , следовательно, на отрезке будет выполнено неравенство . Но это противоречит тому, что на концах отрезка функция имеет значения разных знаков. Аналогично доказывается, что не может быть меньше нуля. Остается принять, что . При этом очевидно, что точка .

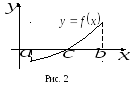Геометрический смысл теоремы заключается в том, что если график непрерывной функции переходит с одной стороны оси на другую, то он обязательно пересекает ось (рис. 53).

Рассмотрим теорему о прохождении непрерывной функции через любое промежуточное значение.

Теорема 4 (вторая теорема Больцано-Коши). Если функция непрерывна на отрезке и на концах его принимает значения и , то для любого числа , заключенного между и : , найдется такая точка , что .

Доказательство. Пусть для определенности и (рис. 54). Рассмотрим вспомогательную функцию . Эта функция непрерывна на отрезке (как разность непрерывных функций) и принимает на концах этого отрезка значения разных знаков:

,

.

По теореме 3 существует точка такая, что . Отсюда .

Следствие 1. Если функция определена и непрерывна на некотором промежутке , то множество ее значений также представляет собой некоторый промежуток.

Геометрическая интерпретация теоремы Больцано-Коши сводится к тому, что для любого числа , заключенного между и , найдется такая внутренняя точка , что , т.е. прямая пересечет график функции , по крайней мере, в одной точке (рис. 3).

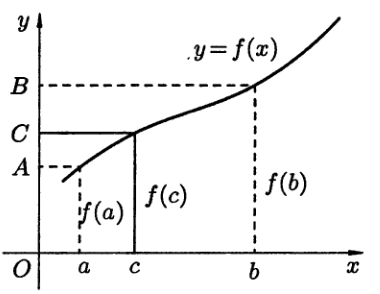
Рис.3.

Таким образом, непрерывная на отрезке функция принимает все промежуточные значения между ее значениями на концах отрезка.

Теоремы 3 и 4 называют теоремами о промежуточных значениях. Они могут быть использованы для приближенного вычисления корней уравнений. Пусть надо решить уравнение .

Следствие 2. Если функция y=f(x) непрерывна на отрезке [a;b] и на его концах принимает значения разных знаков, то внутри отрезка [a;b] найдется хотя бы одна точка c, в которой данная функция f(x) обращается в нуль: f(c)=0

Геометрический смысл теоремы: если график непрерывной функции переходит с одной стороны оси Ох на другую, то он пересекает ось Ох (см. рис. 4).

Следствие 2 лежит в основе так называемого «метода половинного деления», который используется для нахождения корня уравнения f(x)=0.

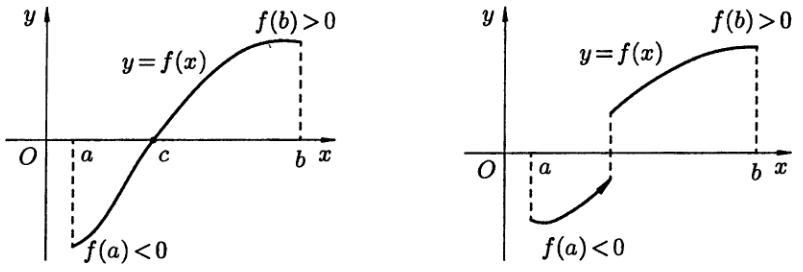
Рис.4. Рис.5.

Утверждения теорем Вейерштрасса и Больцано–Коши, вообще говоря, делаются неверными, если нарушены какие-либо из ее условий: функция непрерывна на отрезке [a;b], а в интервале (a;b), либо функция на отрезке [a;b] имеет разрыв.

Рисунок 5 показывает это для следствия теоремы Больцано-Коши: график разрывной функции не пересекает ось Oх.