1.2.2. Приемы интегрирования уравнений Ньютона

Рассмотрим уравнение движения материальной точки при условии зависимости силы от координат, скорости и времени

.

Обычно рассматривают три частных случая:

1. Сила зависит только от времени, 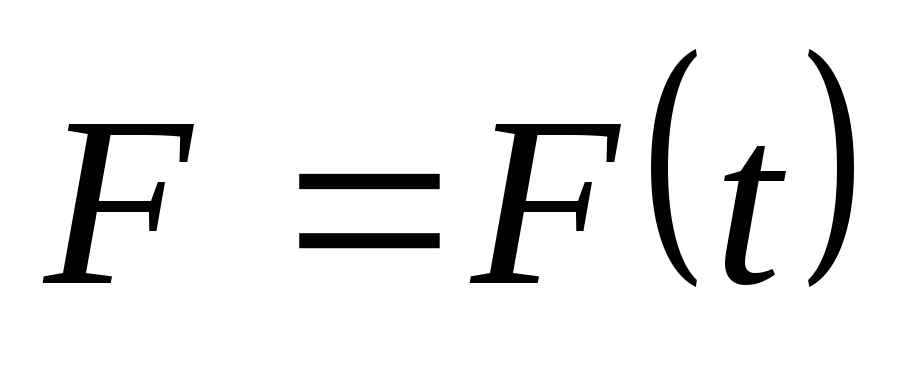, задача решается двукратным интегрированием по времени, (пример - реактивное движение ракеты).

2. Сила зависит только от скорости, 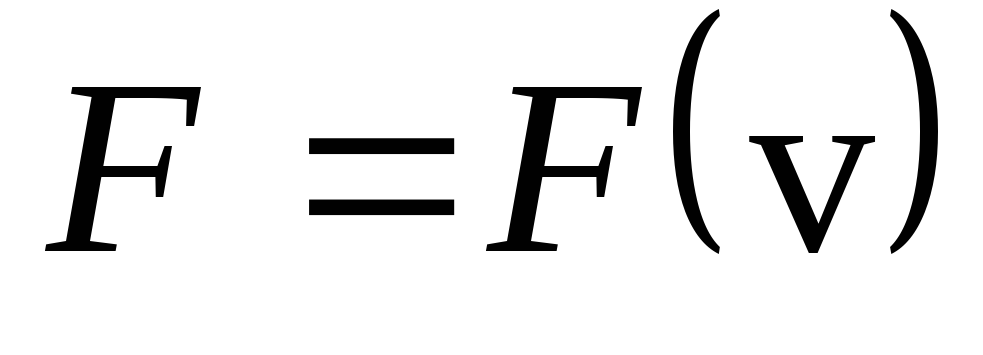. В этом случае для одномерного движения записывая 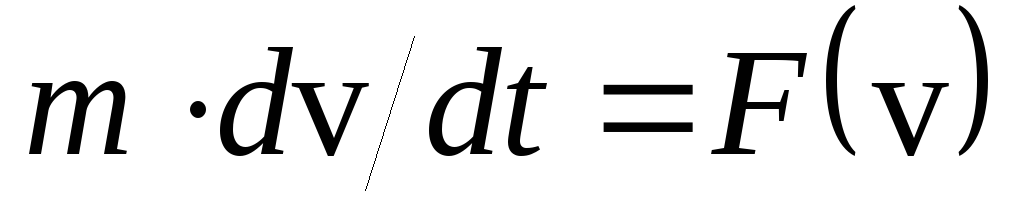, можно разделить переменные, 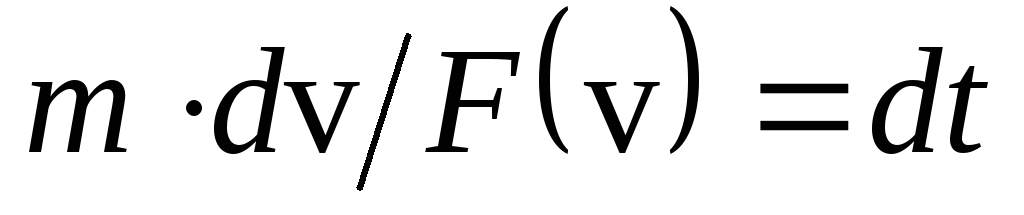и получить зависимость t(v), обращая которую, находим v(t), (пример- движение тела в среде с сопротивлением).

3. Сила зависит только от координат, 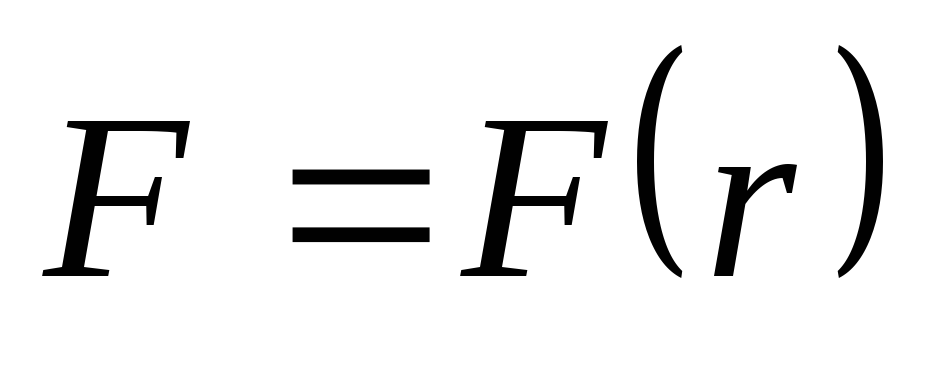, в этом случае интегрирование обычно осуществляется с привлечением закона сохранения момента количества движения и закона сохранения энергии, (классический пример - задача о движении материальной точки в поле центральных сил).

Пример. Вычисление периода колебаний математического маятника.

Запишем закон сохранения энергии для материальной точки, совершающей колебания в вертикальной плоскости под действием силы тяжести: , где: -масса, -длина нити, -угол отклонения нити от вертикали, -максимальный угол отклонения от вертикали.

Разделяя переменные, получим: .

К сожалению, интеграл не вычисляется в элементарных функциях, но легко вычисляется численными методами.

Окончательное выражение для периода колебаний имеет вид 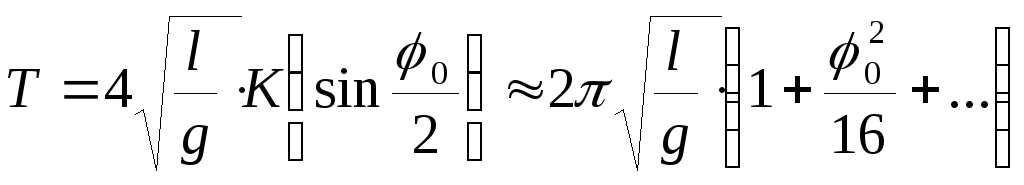, где – полный эллиптический интеграл 1-го рода.

1.2.3. Принцип относительности Галилея

Основывается на следующих постулатах:

1. В любой ИСО пространство однородно и изотропно.

2. Время однородно и абсолютно, т.е. одинаково протекает во всех ИСО. Скорость распространения сигнала может быть бесконечной.

3. Масса частиц одинакова во всех ИСО.

4. Координаты и время в двух ИСО связаны преобразованиями Галилея, , , , - преобразования Галилея.

5. Любое механическое явление, при одинаковых начальных условиях протекает одинаковым образом во всех ИСО (принцип относительности Галилея).

Обоснование принципа относительности Галилея основано на инвариантности величин, входящих в уравнения механики. Величина называется инвариантной, если она не меняется при соответствующих преобразованиях координат, времени. После двукратного дифференцирования преобразований Галилея по времени, получим , т.е. ускорение инвариантно относительно преобразований Галилея. Сила также инвариантна, т.к. она зависит от относительных расстояний и скоростей. Таким образом, все величины, входящие во второй закон Ньютона инвариантны, следовательно, инвариантны и сами уравнения. Окончательно, принцип относительности Галилея можно сформулировать таким образом: все законы классической механики инвариантны относительно преобразований Галилея.

Типовые задачи динамики:

Задача №7. Тормозить или поворачивать? Водитель автомобиля видит стену, перпендикулярную направлению движения. Что меньше: тормозной путь при прямолинейном движении, или минимальный радиус поворота?

Задача №8. Оцените перегрузку, которую испытывает пилот, при посадке на палубу авианосца. Тормозной путь равен 100м, посадочная скорость 216км/час.

Задача №9. Шарик для пинг-понга падает с большой высоты. Чему равно ускорение шарика сразу после отскока от абсолютно упругой поверхности.

Задача №10 (№ 1.59 из сборника задач [5]). Частица движется вдоль оси X по закону , где и – положительные постоянные. В момент t=0 сила, действующая на частицу, равна F₀. найти значение силы F_x в точках поворота и в момент, когда частица опять окажется в точке X=0.

Решение: ; ;

, ; , ; ;

; .

Задача №11 (№ 1.60 из сборника задач [5]). найти модуль и направление силы, действующей на частицу массы m при ее движении в плоскости XY по закону , , где A, B, – постоянные.

Решение: , ;

, ; .

Задача №12 (№ 1.69 из сборника задач [5]). Небольшое тело m начинает скользить по наклонной плоскости из точки, расположенной над вертикальным упором. Коэффициент трения между телом и наклонной плоскостью k=0,14. При каком значении угла время соскальзывания будет наименьшим? Расстояние по горизонтали между точками старта и финиша считать постоянным.

Решение: , очевидно ,

. ;

откуда, после вычисления производной по :

и, окончательно, .

Задача №13 (№ 1.84 из сборника задач [5]). Катер массы m движется по озеру со скоростью V₀. В момент t=0 выключили его двигатель. Считая силу сопротивления пропорциональной скорости катера, , найти:

1. время движения катера с выключенным двигателем;

2. скорость катера в зависимости от пути, пройденного с выключенным двигателем, а также полный путь до остановки.

Решение: ; ; ;

; ; , .

Задача №14 (№ 1.93 из сборника задач [5]). Велосипедист едет по круглой горизонтальной площадке радиуса R. Коэффициент трения зависит только от расстояния r до центра площадки как , где k₀ – постоянная. Найти радиус окружности с центром в точке O, по которой велосипедист может ехать с максимальной скоростью. Какова эта скорость?

Решение: ; ;

; ; .