-
Уравнение (закон) изменения скорости при равнопеременном движении:
,
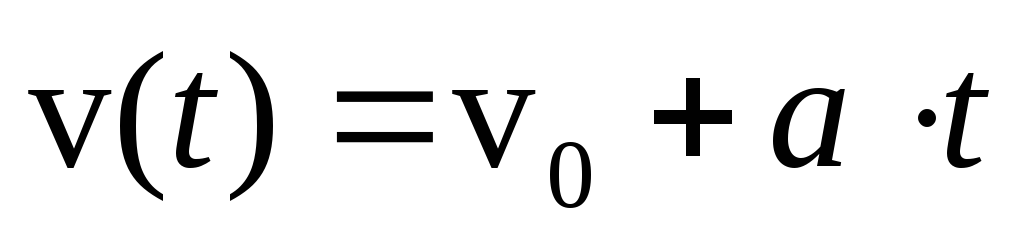или в координатной форме:
-
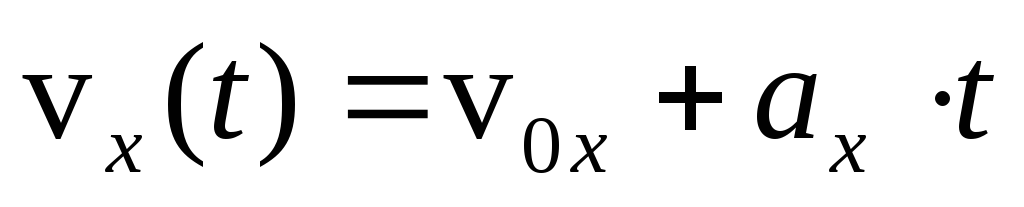
Формула для средней скорости при равнопеременном движении:
. -
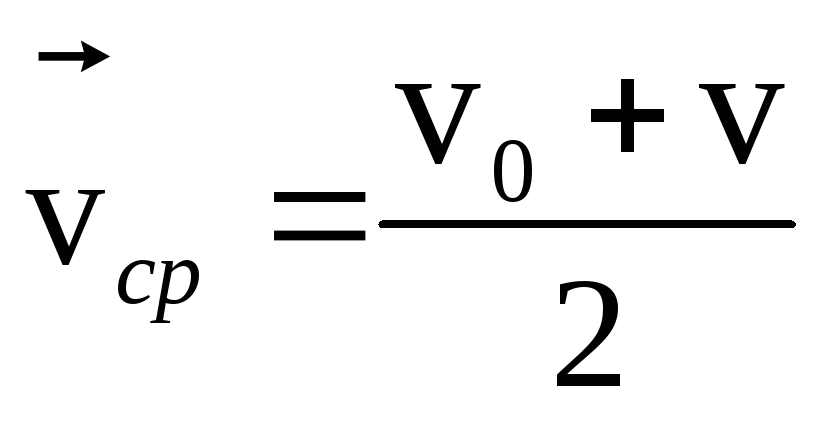П
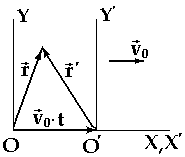
Рис.2
реобразования Галилея, формула сложения скоростей: Пусть имеются две системы отсчета, К и К’, причем К’ движется вдоль положительного направления X с постоянной скоростью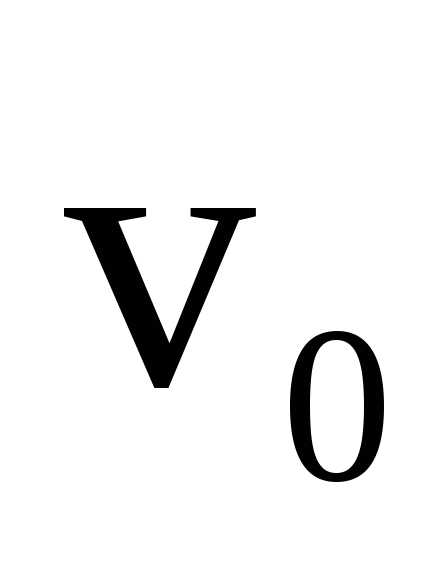
и в начальный момент времени начала
координат совпадали, тогда очевидно
,
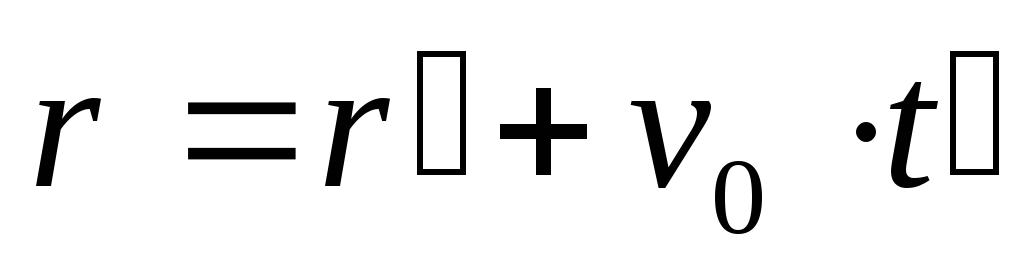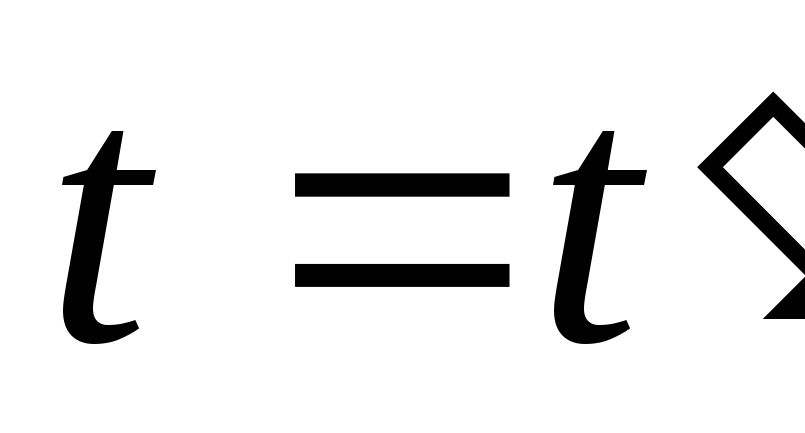- это и есть преобразования координат,
времени Галилея. Продифференцировав
преобразования Галилея по времени,
получим классическую формулу сложения
скоростей
.
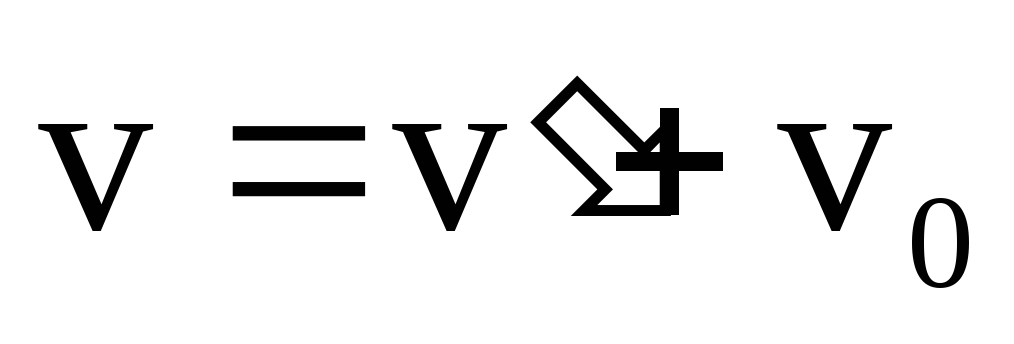Скорость
МТ относительно условно неподвижной
системы отсчета равна векторной сумме
скоростей, относительно подвижной СО
и подвижной СО относительно неподвижной. -
Формула для пути с исключенным временем: .
Основные определения кинематики вращательного движения:
18.
Период
– это
значение интервала времени, за который
тело совершает полный оборот по
циклической траектории.
Частота –
величина обратная периоду,
,
.
Число
оборотов в секунду равно частоте, но
обозначается n,
.
19.
Угловая
скорость
– скалярная величина, равная первой
производной угла поворота по времени,
.
Далее мы введем угол и угловую скорость
как векторные величины. При равномерном
движении
.
20. Ускорение при криволинейном движении – имеет две составляющие: тангенциальную, отвечающую за изменение скорости по величине и нормальную, или центростремительную, отвечающую за искривление траектории
С
учетом выражения
окончательно
получаем:
,
,
где
-единичный
вектор, направленный к центру кривизны,
- единичный вектор вдоль касательной к
траектории. Более компактный вывод
выглядит так:
,
следовательно,
и
.
Типичные
задачи
кинематики:
Задача №2. Чему равна скорость точек A,B,C,D на диске, рис.4, катящемся по плоскости без проскальзывания (чистое качение). Изобразите геометрическое место точек диска, у которых скорость по модулю равна скорости поступательного движения диска.
Задача № 3. Два автомобиля едут в попутном направлении с заданной скоростью. На какой минимальной дистанции необходимо держаться второму автомобилю, чтобы обезопасить себя от попадания камней, вырывающихся из-под колес первого автомобиля. Под каким углом к горизонту в системе отсчета, связанной с землей вылетают самые опасные камни? Сопротивлением воздуха пренебречь.
Ответ:
,
- вперед по ходу движения.
Задача
№ 4. Критическое
для тела человека кратковременное
ускорение (при котором есть шанс избежать
серьезных травм) равно
.
Каким должен быть минимальный тормозной
путь, если начальная скорость автомобиля
равнялась 100км/ч?
Задача
№ 5. (№1.23
из сборника задач [5]).
Точка
движется, замедляясь, по прямой с
ускорением, модуль которого зависит от
ее скорости
по закону
,
где
- положительная постоянная. В начальный
момент скорость точки равна
.
Какой путь она пройдет до остановки?
За какое время этот путь будет пройден?
Решение:
записывая выражение для модуля ускорения
и, разделяя переменные, получим:
.
Интегрируя с учетом начального условия
,
получим:
.
Остановке соответствует момент
времени
.
Интегрируя
выражение для скорости, получаем
.
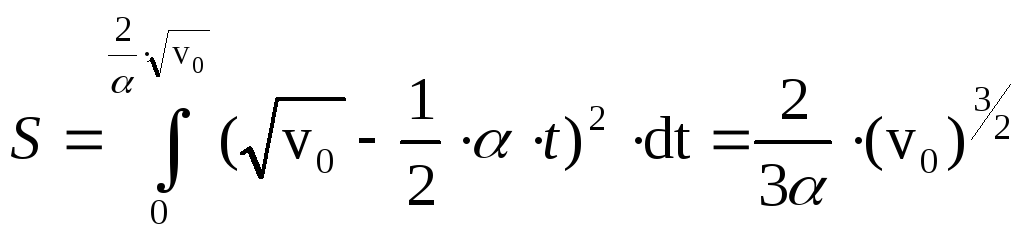Ответ:
.
Задача
№6 (№
1.39 из сборника задач [5]). Точка движется
по дуге окружности радиуса R. Ее скорость
зависит от пройденного пути S по закону
,
где
– постоянная. Найти угол
между вектором полного ускорения и
вектором скорости в зависимости от S.
Решение:
.
Разделив переменные и проинтегрировав,
получим:
;
;
;
;
.
Вопросы для контроля:
-
Можно ли утверждать, что каждая частица покоится в собственной системе отсчета?
-
Можно ли утверждать, что ускорение автомобиля равно нулю, если спидометр все время показывает одно и тоже значение?
-
В какой точке траектории снаряд имеет наименьшую скорость?
-
В чем ошибочность утверждения, что равнопеременное движение – это движение с постоянным по величине ускорением?
-
Как вы себе представляете синхронизацию часов, находящихся в разных частях пространства?
-
Можно ли по уравнению траектории восстановить уравнение движения тела?
-
Могут ли вектора скорости и ускорения составлять между собой тупой угол?
-
Как связаны между собой линейная и угловая скорость? Тангенциальное и угловое ускорения?
-
В каких системах отсчета выполняется классическое правило сложения скоростей?
-
В чем суть преобразований Галилея?