Взаємне розташування прямої та площини.

Розглянемо основні задачі про взаємне розташування прямої та площини.

1. Знайти точку перетину прямої 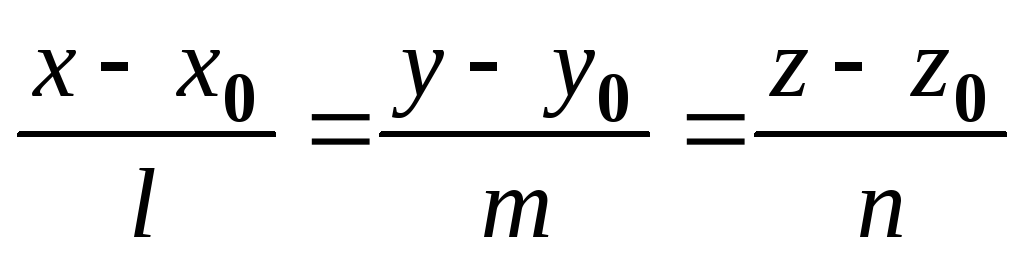з площиною .

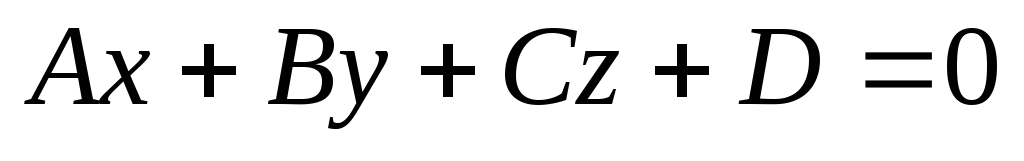Використаємо рівняння прямої у параметричній формі (1) та підставимо їх у рівняння площини. Таким чином з’ясуємо, при якому значенні параметру має місце перетин прямої з площиною. Визначивши таким чином коефіцієнт , знайдемо координати точки перетину прямої та площини.

Приклад 4. Знайти точку перетину прямої з площиною .

Підставимо параметричні рівняння прямої у рівняння площини: , звідки . Отже, – точка перетину даної прямої з площиною.

2. Знайти кут між прямою 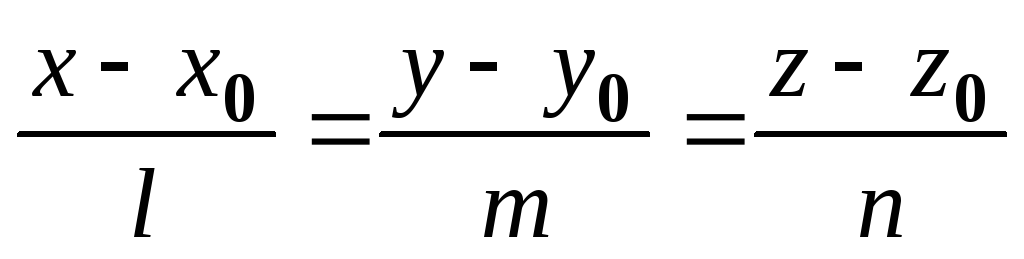та площиною 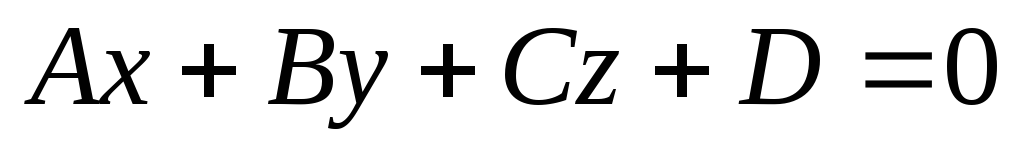.Сформулювати умови їх паралельності та ортогональності.

Неважко зрозуміти, що або , де – це кут між нормаллю площини та напрямним вектором прямої. Тому . Пряма та площина паралельні, коли , а перпендикулярні – при , тобто .

Приклад 5. Знайти кут між прямою та площиною .

Тут – напрямний вектор прямої, а – нормаль площини. Тоді

3. Сформулювати умови належності прямої 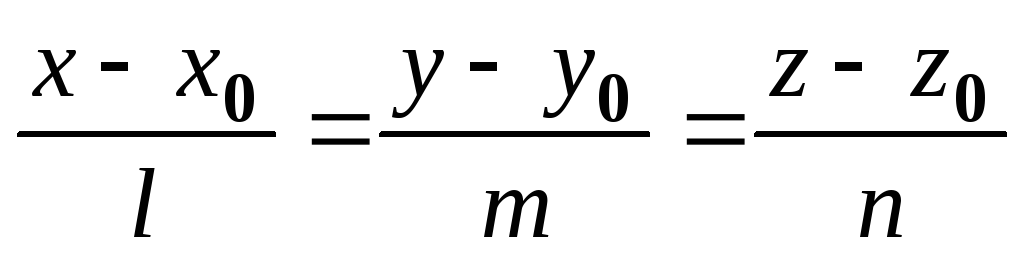до площини .

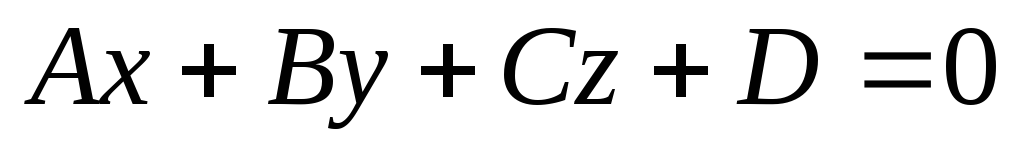Для того, щоб пряма лежала у площині необхідно і достатньо виконання двох умов: пряма паралельна площині і одна точка прямої належить площині. Запишемо ці умови аналітично: .

4. Сформулювати умови перетину двох непаралельних прямих 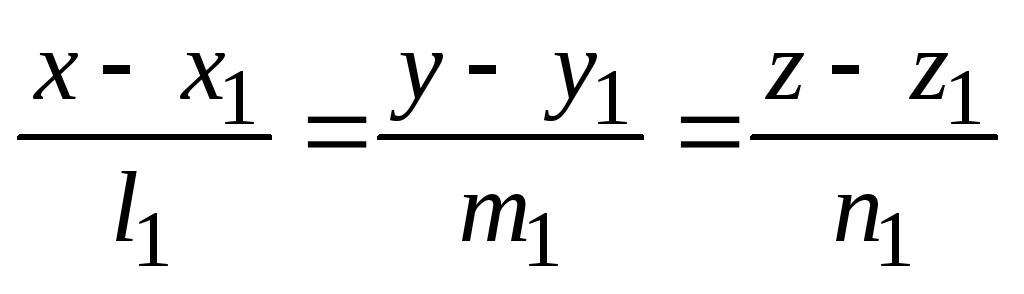та .

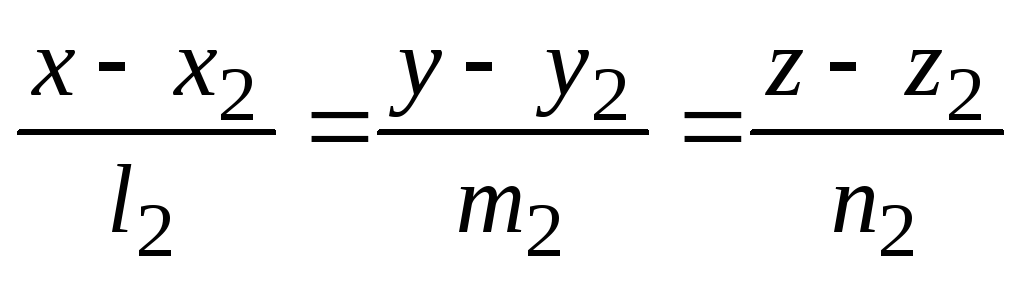Переконайтесь самостійно, що умова перетину двох непаралельних прямих еквівалентна умові компланарності векторів , та , де та .

5. Записати рівняння площини, що проходить через дві задані паралельні прямі.

6. Записати рівняння площини, що проходить через дві задані прямі, що перетинаються.

7. Знайти точку симетричну заданій відносно заданої площини.

Приклад 6. Знайти точку, симетричну точці відносно площини .

Опустимо перпендикуляр із точки на площину та знайдемо точку перетину його з площиною. Точка

буде серединою відрізку , де – шукана симетрична точка. Отже, перпендикуляр має проходити через точку , а його напрямним вектором буде нормаль заданої площини. Таким чином одержимо рівняння цього перпендикуляра: . Точку знайдемо, як описано в прикладі 4: . Далі, оскільки точка – середина відрізку , то її координати є напівсумою відповідних координат точок та , звідки й знаходимо .

8. Знайти відстань між двома заданими паралельними прямими.

9. Знайти відстань до заданої прямої від точки, що не лежить на даній прямій.

Приклад 7. Знайти відстань точки від прямої .

Побудуємо площину, що проходить через точку перпендикулярно до заданої прямої: , або . Відшукаємо точку перетину цієї площини із заданою прямою: . Шукана відстань дорівнює довжині відрізку : .

6