10

Функции многих переменных.

Изучение различных законов природы приводит к понятию функции многих переменных. Например, объем параллелепипеда V = xyz, т.е. является функцией трех переменных. Кинетическая энергия есть функция массы и скорости точки

T = m v²_{/ 2.}

Определение. Переменная z называется функцией от переменных x и у, если по некоторому правилу или закону каждой паре значений х и у из некоторой области их изменения D ставится в соответствие определенное значение z.

Символически функция нескольких переменных обозначается так

z = f(x, y), u = F(x, y,z) и т.д.

Область (D) называется областью определения функции.

Существуют следующие способы задания функции.

1. Аналитический. Зависимость между аргументами задается с помощью формулы

z = x² + y², W = sin^u/_v + x² – ln (y + z) и т.д.

2. Табличный. Зависимость между х и у задается в виде таблицы с двумя входами.

x y y₁ y₂ ... y_m

x₁ z₁₁ z_{12 .....} z_1m

x₂ z₂₁ z₂₂ .... z_2m

..............................................

x_n z_n1 z_n2 .... z_{n m}

3. Графический. Уравнение z = f(x, y) определяет в пространстве поверхность, которая называется графиком функции.

. Например, z = x² + y². Графиком является параболоид вращения.

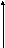z

y

x

Совокупность пар значений х и у, в которых функция имеет смысл, называют областью определения функции. Если каждую пару (х,у) изображать точкой плоскости Oxy, то область определения функции z = f(x,y) изобразится как некоторая совокупность плоскости. y

Например y x

Предел, непрерывность.

Для функции многих переменных справедливо определение предела переменной величины, данное ранее.

Функция f(x,y) называется непрерывной в точке х = х₀, у = у₀, если она определена в этой точке и

Частные производные.

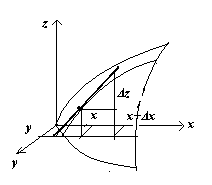f(x + ∆x, y) – f(x, y) = ∆_xz – частное приращение функции по х. Найдем

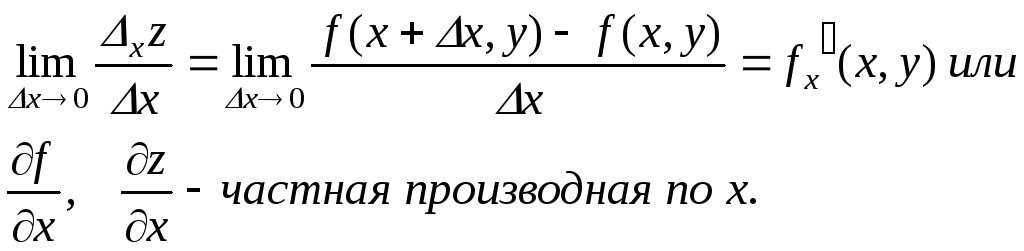
Аналогично определяется частная производная по у.

f(x, y + - частное приращение по у.

Полное приращение и полный дифференциал функции.

∆z = f(x + ∆x, y + ∆y) – f(x,y) – полное приращение

(x + ∆x, y + ∆y) функции.

ρ Пусть функция f(x, y) и ее производные f′_x (x, y),

. (х, у) f′_y(x, y) непрерывны в некоторой окрестности

х точки (x, y).

Определения.

1. Дифференциалами независимых переменных x и у называются их приращения и обозначаются dx = Δx и dy = Δy/

2. Частными дифференциалами функции f(x, y) называются выражения

3. Полным дифференциалом функции f(x, y) называется выражение

Можно показать, что полное приращение функции связано с полным дифференциалом

следующим соотношением

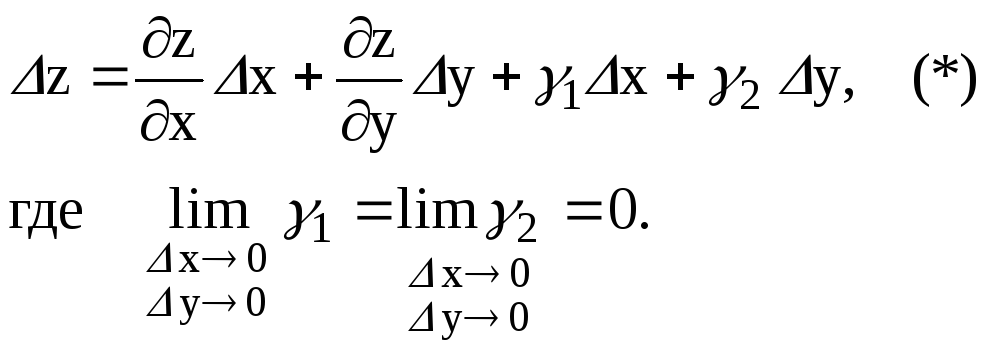
Пусть Очевидно, ρ→0 при Δx→0 и Δy→0.

Рассмотрим

- бесконечно малая более высокого порядка, чем ρ.

Следовательно, полное приращение функции отличается от полного дифференциала на бесконечно малую высшего порядка, чем ρ = .