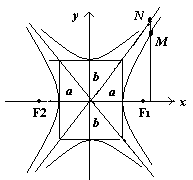
Гипербола.

Гиперболой называется геометрическое место точек, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2a.

F₂M – F₁M = . Обозначим F₂F₁ = 2c, 2a < 2c, a < c.

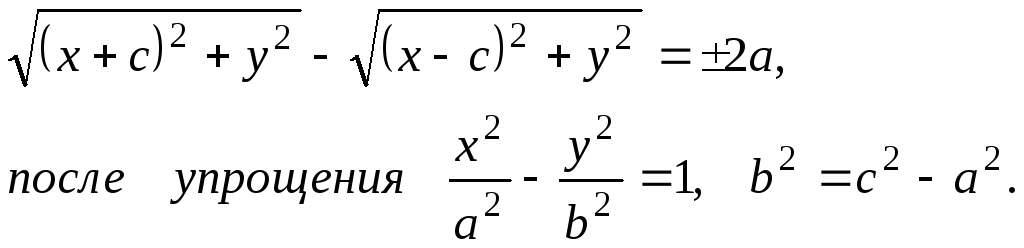
Точки пересечения с осями координат - y = 0, x = .

x = 0 – точек пересечения с осью оу нет.

Оси координат являются осями симметрии гиперболы

Пусть x ≥ 0, y ≥ 0. . Отсюда |x| ≥ a .

y_min= 0 при x = a, у возрастает при возрастании х. Прямые

называются асимптотами гиперболы. − сопряженная гипербола. Парабола.

Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом и от данной прямой, называемой директрисой.

MF = MD, KF = p, Другие виды параболы

y² = 2px -каноническое уравнение параболы. y² = -2px x² =2py x² = -2py

Ох – ось симметрии, x ≥ 0, .

Общее уравнение кривых второго порядка.

В общем уравнении кривых второго порядка положим В = 0. Тогда уравнение принимает вид

Ax² + Cy² + 2Dx + 2Ey + F = 0.

1. AC >0 – уравнение эллиптического типа, определяет, вообще говоря, эллипс со смещенным центром и осями симметрии, параллельными осям координат, или случаи его вырождения. Уравнение приводится к виду

y b

a a

y₀

b

x

x₀

2. АС < 0 – уравнение гиперболического типа, определяет, вообще говоря, гиперболу со смещенным центром и осями симметрии, параллельными осям координат, или случаи ее вырождения. Уравнение приводится к виду

y

b

b

y₀ a a

b

x₀ x

3. AC = 0 – уравнение параболического типа, определяет, вообще говоря, параболу со смещенной вершиной и осью симметрии, параллельной той оси, при которой нет квадрата в уравнении или случаи ее вырождения.

3.1. A = 0, D ≠ 0. Уравнение приводится к виду и определяет параболу с осью симметрии, параллельной оси x.

y -^C/_2D > 0 y

O₁ -^C/_2D> 0

x x

-^C/_2D < 0

-^C/_2D < 0 O₁

3.2. C = 0, E ≠ 0. Уравнение приводится к виду и определяет параболу с осью симметрии, параллельной оси y.

П р и м е р ы. Определить вид и построить кривую.

1. 4x² – y² – 8x + 4y – 4 = 0. 4(x² – 2x + 1 – 1) –(y² – 4y + 4 – 4) – 4 = 0, 4(x −1)² – (y – 2)² = 4,

y

Гипербола,

O₁(1, 2), a = 1, b = 2. 2

1 x

2. 2x² + 4x + y = 0, y = -2x² – 4x − парабола, координаты вершины x₀ = -1, y₀ = 2,

y Ось симметрии параллельна оси ox, ветви направлены в

O₁(-1, 2)

вниз. Точки пересечения с осями координат:

y = 0, x₁ = 0, x₂ =-2.

o x