1.8. Алгебра линейных операторов.

В этом разделе мы рассмотрим алгебраические операции, позволяющие по известным линейным операторам получать новые линейные операторы.

1) Сумма линейных операторов.

Если и - линейные операторы, действующие из пространства в пространство , то однозначно определен линейный оператор , называемый суммой операторов и так, что

Тем самым оператор , как функция, определен стандартно как сумма функций.

2. Умножение линейного оператора на число.

Если - линейный оператор, и - вещественное число, то оператор , называемый результатом умножения на число , определяется так:

Линейность нового оператора также очевидна. Ясно и то, что .

Легко доказать, что операции сложения и умножения на число обладают следующими свойствами:

1. 

2. 

3. существует линейный оператор такой, что для любого

4. для каждого линейного оператора 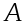существует линейный оператор такой, что

5. 

6. 

7. 

8. 

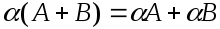
В записанных выше тождествах суть произвольные линейные операторы, действующие из некоторого линейного пространства в некоторое линейное пространство . Оператор , называемый нулевым оператором, определяется так:

(т.е. этот оператор каждый вектор отображает в нулевой вектор).

Оператор , называемый противоположным к , определен как , т.е.

Через противоположный оператор, как и в случае векторов, определяется разность линейных операторов:

Итак, мы получаем, что множество всех линейных операторов, действующих из в , само является линейным пространством. Это линейное пространство будем обозначать .

В частности, если - какое-то линейное пространство, а - множество вещественных чисел, определенное как одномерное арифметическое векторное пространство, то линейное пространство называется линейным пространством, сопряженным к , и обозначается . Элементы сопряженного пространства называются линейными функционалами, или ковекторами. Позже мы изучим структуру этого пространства (в конечномерном случае) подробнее.

Продолжим рассмотрение операций над линейными операторами.

3) Композиция линейных операторов.

Если и - линейные операторы, то в этом случае (а именно, когда область значений оператора содержится в области определения оператора ) определен оператор , называемый композицией (или произведением) на :

Таким образом, композиция линейных операторов - это обычная композиция функций. Линейность нового оператора легко доказывается.

Пусть - множество всех линейных преобразований некоторого линейного пространства . Тогда для любых операторов (преобразований) из имеют место следующие тождества:

1. 

2. 

3. , где - тождественное преобразование:

4. (для любого вещественного ).

5. 

Стандартное доказательство этих тождеств опускается. Можно заметить аналогию приведенных алгебраических законов с алгеброй матриц. Мы увидим, что это не случайно. Заметим также, что тождества (1), (2), (4) имеют место для любых линейных операторов подходящих типов.

4) Обратный линейный оператор.

Пусть - линейный оператор. Если определен такой линейный оператор , что , то он называется обратным к .

Из определения сразу следует, что если обратный оператор определен, то

В частности, если (т.е., рассматриваются линейные преобразования), то можно написать двойное тождество

Утверждение 1.8 Если обратный линейный оператор существует, то он - единственный.

Доказательство. Предположим, что существуют два линейных оператора и , обратных к . Тогда:

, где через обозначено тождественное преобразование пространства , .

Пусть - линейное преобразование пространства . Линейное преобразование назовем левым обратным к , если

.

Аналогично определяется линейное преобразование, правое обратное к :

.

Как и для матриц доказывается

Утверждение 1.9 Если для линейного преобразования существует левое и правое обратное преобразования, то они равны и совпадают с обратным к .

Доказательство. Имеем:

.

Доказанное утверждение можно распространить и на произвольный линейный оператор , но тогда - тождественное преобразование пространства , соответственно - тождественное преобразование пространства .

Доказанное только что позволяет нам ввести обозначение для линейного оператора, обратного к .

Определение 1.14 Линейный оператор называется обратимым, если существует обратный к нему линейный оператор.

Основным результатом настоящего раздела является следующая теорема:

Теорема 1.2 (Критерий обратимости линейного оператора). Линейный оператор обратим тогда и только тогда, когда он является изоморфизмом на .

Доказательство. 1) Необходимость. Если оператор обратим, то его ядро тривиально, т.е. состоит из одного нулевого вектора. Действительно, пусть для некоторого ненулевого . Тогда , что невозможно. Следовательно, , и - мономорфизм. Полагая теперь, что , получим для некоторого , откуда - в противоречии с предположением. Окончательно получаем, что - изоморфизм.

2) Достаточность. Пусть - изоморфизм. Тогда для каждого существует единственный такой, что .

Введем отображение так, что

Другими словами, мы определили такое отображение из в , что образ есть тот самый (единственный в силу того, что изоморфизм!) , для которого :

(здесь использовано так называемое «йота-обозначение», или «йота-оператор»:означает «тот единственный , для которого истинно »).

Из определения отображения сразу следует, что

Это значит, что осталось только показать, что отображение линейно.

Имеем: для произвольных пусть , а . Тогда

Совершенно аналогично доказывается, что (для любого вещественного ).

Итак, отображение линейно и, следовательно, .

Теорема доказана.

Следствие 1.1 Если - изоморфизм, то - также изоморфизм.

Следствие 1.2 Композиция изоморфизмов есть изоморфизм, причем для изоморфизмов .

Определение 1.15 Линейные пространства и называются изоморфными, если существует изоморфизм одного из них на другое.

Для изоморфных пространств будем писать . На основании доказанного выше мы можем утверждать:

1. 

2. 

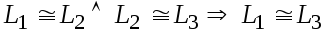
3. для всякого .

Содержательно тот факт, что два линейных пространства изоморфны, означает, что между этими пространствами можно установить такое взаимно однозначное соответствие , что для любых векторов одного из этих пространств

,

т.е., с точки зрения линейных операций над векторами, эти пространства неразличимы. Тогда, например, если вычисления удобнее выполнять в каком-то одном пространстве, то эти вычисления можно выполнить именно в этом пространстве, а получив результат, «вернуться» в другое пространство.

Оказывается, любое конечномерное линейное пространство совпадает «с точностью до изоморфизма» с арифметическим векторным пространством для подходящего .

Теорема 1.3 Конечномерное линейное пространство , размерность которого изоморфно арифметическому пространству .

Доказательство. Выберем в пространстве какой-то базис и разложим по нему произвольно выбранный вектор :

Отображение зададим тогда так:

,

т.е., любому вектору сопоставляется столбец его координат в некотором базисе. Ясно, что относительно фиксированного базиса отображение взаимно однозначно. Линейность его также легко проверяется.

Итак, в силу доказанной теоремы, если отождествлять изоморфные линейные пространства, то любое конечномерное линейное пространство совпадает с пространством арифметических векторов подходящей размерности.

Например, в пространстве матриц система матриц, где ,

образует базис.

Следовательно, .

Заметим еще, что если отождествлять конечномерное линейное пространство с изоморфным ему арифметическим, то исчезает и принципиальное различие между мономорфизмом и изоморфизмом.

Действительно, если мономорфизм рассматривать как изоморфизм на , то при получим цепочку изоморфизмов:

,

что дает нам право считать мономорфизм изоморфизмом арифметического пространства на себя.