
- •Глава 1. Элементы линейной алгебры
- •1.1. Понятие линейного пространства
- •Единственность нулевого вектора
- •Единственность противоположного вектора
- •Результат умножения на нуль
- •Результат умножения на
- •Результат умножения произвольного числа на нулевой вектор
- •1.2. Линейно зависимые и линейно независимые системы векторов. Базис и размерность.
- •1.3. Подпространства и линейные оболочки
- •1.4. Преобразования базисов
- •1.5. Вещественное евклидово пространство
- •1.6. Ортогональные системы векторов
- •1.7. Линейные операторы
- •1.8. Алгебра линейных операторов.
- •1.9. Матрица линейного оператора
- •1.10. Ортогональное дополнение
- •1.11. Собственные векторы и собственные числа линейного оператора.
- •1.12. Линейные формы
- •1.13. Билинейные и квадратичные формы
- •1.14. Сопряженный оператор. Самосопряженность
- •1.15. Ортогональные матрицы и ортогональные преобразования
- •1.16. Квадратичные формы в евклидовых пространствах. Закон инерции
- •1.17.Знакоопределенные квадратичные формы. Критерий Сильвестра.
- •1.18. Гиперповерхности второго порядка
- •1.19. Норма линейного оператора
1.3. Подпространства и линейные оболочки
Определение 1.3
Подмножество
![]() линейного пространства
линейного пространства
![]() называется подпространством
пространства
называется подпространством
пространства
![]() ,
если вместе с любыми двумя векторами
оно содержит их сумму, а вместе с любым
вектором - результат умножения его на
любое число.
,
если вместе с любыми двумя векторами
оно содержит их сумму, а вместе с любым
вектором - результат умножения его на
любое число.
Утверждение 1.1
Подмножество
![]() линейного пространства
линейного пространства
![]() является подпространством
является подпространством
![]() тогда и только тогда, когда для любой
системы векторов в
тогда и только тогда, когда для любой
системы векторов в
![]() оно
содержит их произвольную линейную
комбинацию.
оно
содержит их произвольную линейную
комбинацию.
Доказательство. Упражнение.
Примеры.
1) В пространстве
![]() всех
геометрических векторов подмножество
всех векторов, параллельных некоторой
плоскости, будет подпространством, а
подмножество всех векторов, концы
которых лежат на некоторой плоскости,
не будет подпространством.
всех
геометрических векторов подмножество
всех векторов, параллельных некоторой
плоскости, будет подпространством, а
подмножество всех векторов, концы
которых лежат на некоторой плоскости,
не будет подпространством.
2) Множество всех
решений однородной линейной системы
есть, как мы видели в первом семестре,
векторное пространство, которое будет
ни чем иным, как подпространством
арифметического пространства
![]() (где
(где
![]() в данном случае есть число неизвестных
системы).
в данном случае есть число неизвестных
системы).
3) В пространстве
![]() рассмотрим подмножество всех многочленов
степени, не превосходящей некоторого
фиксированного
рассмотрим подмножество всех многочленов
степени, не превосходящей некоторого
фиксированного
![]() .
Сумма любых двух таких многочленов
снова есть многочлен из заданного
множества, равно как и результат умножения
такого многочлена на произвольное число
остается в данном множестве многочленов.
Следовательно, множество многочленов
степени не выше
.
Сумма любых двух таких многочленов
снова есть многочлен из заданного
множества, равно как и результат умножения
такого многочлена на произвольное число
остается в данном множестве многочленов.
Следовательно, множество многочленов
степени не выше
![]() является подпространством пространства
является подпространством пространства
![]() .
Можно доказать, что система многочленов
.
Можно доказать, что система многочленов
![]() является
базисом этого подпространства
(упражнение!), и, таким образом, размерность
данного подпространства многочленов
равна
является
базисом этого подпространства
(упражнение!), и, таким образом, размерность
данного подпространства многочленов
равна
![]() .
Мы имеем здесь, стало быть, пример
конечномерного подпространства
бесконечномерного линейного пространства.
.
Мы имеем здесь, стало быть, пример
конечномерного подпространства
бесконечномерного линейного пространства.
Определение 1.4
Линейной оболочкой
системы векторов
![]() некоторого линейного пространства
некоторого линейного пространства
![]() называется множество всех линейных
комбинаций векторов системы.
называется множество всех линейных
комбинаций векторов системы.
Линейную оболочку
будем обозначать
![]() .
По определению тогда
.
По определению тогда
![]()
В первом семестре мы определили понятие ранга системы векторов как наибольшего числа линейно независимых векторов системы. Нетрудно доказать следующий результат:
Утверждение 1.2 Ранг системы векторов равен размерности ее линейной оболочки.
Примеры. 1) В
пространстве геометрических векторов
возьмем систему векторов, состоящую из
некоторых двух ненулевых и неколлинеарных
векторов
![]() .
Тогда
.
Тогда
![]() (для
произвольных вещественных
(для
произвольных вещественных
![]() и
и
![]() ).
Геометрически это множество векторов,
параллельных плоскости векторов
).
Геометрически это множество векторов,
параллельных плоскости векторов
![]() (любые два неколлинеарных вектора могут
быть «положены» в некоторую плоскость,
определенную однозначно с точностью
до параллельного
(любые два неколлинеарных вектора могут
быть «положены» в некоторую плоскость,
определенную однозначно с точностью
до параллельного
переноса) - см. рис. 1.1.









Рис. 1.1
2) Пространство
многочленов, рассмотренное выше, есть
линейная оболочка системы степенных
функций
![]() .
.
1.4. Преобразования базисов
Пусть задан в линейном
пространстве
![]() некоторый базис
некоторый базис
![]() .
Тогда любой вектор
.
Тогда любой вектор
![]() может быть разложен единственным образом
по базису (материал первого семестра!):
может быть разложен единственным образом
по базису (материал первого семестра!):
![]()
Введем новый базис
![]() .
В этом базисе тот же самый вектор
.
В этом базисе тот же самый вектор
![]() будет иметь уже другие координаты:
будет иметь уже другие координаты:
![]()
Возникает задача: связать между собой координаты произвольного вектора в двух различных базисах. Эту задачу будем называть задачей преобразования базисов.
Чтобы технически удобно решить эту задачу и подобные ей, введем в рассмотрение новый объект - векторную матрицу-строку. Это обычная матрица-строка, но ее элементами являются не числа, а векторы (из некоторого линейного пространства). Любую систему векторов можно задать в виде векторной матрицы строки.
Для векторной
матрицы-строки
![]() определим умножение ее справа на обычную
числовую матрицу
определим умножение ее справа на обычную
числовую матрицу
![]() размера
размера
![]() для данного
для данного
![]() ,
равного числу векторов строки и
произвольного
,
равного числу векторов строки и
произвольного
![]() следующим образом:
следующим образом:
![]()
Таким образом, по
определению, результатом умножения
векторной матрицы строки справа на
числовую матрицу будет новая векторная
матрица-строка, число компонент которой
равно числу столбцов матрицы
![]() ,
и каждая компонента вычисляется как
умножение векторной строки на
соответствующий столбец числовой
матрицы по тому же правилу, что и в
обычном матричном умножении, но только
вместо числового умножения используется
умножение вектора на число.
,
и каждая компонента вычисляется как
умножение векторной строки на
соответствующий столбец числовой
матрицы по тому же правилу, что и в
обычном матричном умножении, но только
вместо числового умножения используется
умножение вектора на число.




Легко доказать (по аналогии с доказательством ассоциативности умножения числовых матриц) следующее равенство:
![]() (каковы бы ни были
числовые матрицы
(каковы бы ни были
числовые матрицы
![]() и
и
![]() ,
произведение которых существует).
,
произведение которых существует).
С использованием векторных матриц-строк удобно записывать разложение произвольных систем векторов по данному базису.
Пусть дан базис (в
виде векторной матрицы-строки)
![]() и система векторов
и система векторов
![]() .
Запишем разложение векторов системы
.
Запишем разложение векторов системы
![]() по базису
по базису
![]() :
:

Или, с использованием векторных матриц-строк:
![]()
Нетрудно сообразить,
что j-ый
столбец матрицы
![]() - это столбец координат вектора
- это столбец координат вектора
![]() в базисе
в базисе
![]() .
.
Утверждение 1.3
Если система
![]() линейно независима, то столбцы матрицы
линейно независима, то столбцы матрицы
![]() линейно независимы.
линейно независимы.
Доказательство.
Предположим противное - тогда найдутся
числа
![]() ,
не все равные нулю, такие, что
,
не все равные нулю, такие, что
 ,
,
или, покомпонентно:

С учетом этих равенств рассмотрим линейную комбинацию
![]()
Подставляя вместо
каждого вектора
![]() ,
его разложение по базису
,
его разложение по базису
![]() ,
получим:
,
получим:

Итак, мы получили нетривиальную линейную комбинацию линейно независимых векторов, равную нулю, что невозможно.
Можно заметить, что,
проводя рассуждения доказательства
утверждения 1.3 в обратном порядке,
получим, что верно и обратное: если
столбцы матрицы
![]() линейно
независимы, то система векторов
линейно
независимы, то система векторов
![]() линейно
независима. Следовательно, для
распознавания линейной независимости
произвольной системы векторов
конечномерного линейного пространства
достаточно составить матрицу из столбцов
координат векторов системы в произвольном
фиксированном базисе и доказать линейную
независимость этих столбцов, используя,
например, метод элементарных преобразований
(т.е., вычислив ранг составленной
матрицы).
линейно
независима. Следовательно, для
распознавания линейной независимости
произвольной системы векторов
конечномерного линейного пространства
достаточно составить матрицу из столбцов
координат векторов системы в произвольном
фиксированном базисе и доказать линейную
независимость этих столбцов, используя,
например, метод элементарных преобразований
(т.е., вычислив ранг составленной
матрицы).
Для одного вектора
![]() его разложение по базису задается в
виде:
его разложение по базису задается в
виде:
![]() ,
где
,
где
![]() -
столбец координат вектора
-
столбец координат вектора
![]() в базисе
в базисе
![]() .
.
Вернемся к задаче преобразования базисов. Запишем разложение нового («штрихованного») базиса в старом (не «штрихованном»):
![]()
Матрица
![]() (квадратная порядка
(квадратная порядка
![]() )
называется матрицей
перехода от
базиса
)
называется матрицей
перехода от
базиса
![]() к
базису
к
базису
![]() .
Каждый ее столбец есть, как мы только
что доказали, столбец координат
соответствующего вектора нового базиса
в старом базисе. В силу утверждения 1.3
столбцы матрицы
.
Каждый ее столбец есть, как мы только
что доказали, столбец координат
соответствующего вектора нового базиса
в старом базисе. В силу утверждения 1.3
столбцы матрицы
![]() линейно
независимы, тем самым ее ранг равен
линейно
независимы, тем самым ее ранг равен
![]() ,
и матрица
,
и матрица
![]() является
невырожденной.
является
невырожденной.
Тогда для разложения
вектора
![]() в новом базисе получим:
в новом базисе получим:
![]()
Отсюда по теореме о единственности разложения вектора по базису (первый семестр!)
![]()
Так как матрица
![]() не вырождена, то
не вырождена, то
![]()
Итак, чтобы вычислить столбец координат вектора в новом базисе, достаточно матрицу, обратную к матрице перехода, умножить на столбец координат вектора в старом базисе.
По контрасту заметим, что для того, чтобы получить сам новый базис (как векторную матрицу-строку), нужно старый базис умножить на саму матрицу перехода.
Таким образом, можно заметить, что сами базисы и координаты векторов в базисах при переходе от базиса к базису перевычисляются «зеркально» по отношению к друг другу.
Утверждение 1.4
1) Если
![]() -
матрица перехода от базиса
-
матрица перехода от базиса
![]() к
базису
к
базису
![]() ,
то обратная матрица
,
то обратная матрица
![]() является матрицей перехода от базиса
является матрицей перехода от базиса
![]() к базису
к базису
![]() .
.
-
Если
 -
матрица перехода от базиса
-
матрица перехода от базиса
 к
базису
к
базису
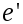 ,
а
,
а
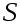 -
матрица перехода от базиса
-
матрица перехода от базиса
 к
базису
к
базису
 ,
то
,
то
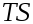 -
матрица перехода от базиса
-
матрица перехода от базиса
 к базису
к базису
 .
.
Схематически:
Т T S
![]()




![]()
![]()
![]()
![]()


 T-
-1
T-
-1
TS
Доказательство. Упражнение.
Со сложными
преобразованиями базисов связана
следующая задача: пусть векторы базисов
![]() и
и
![]() заданы
своими координатами в некотором базисе
заданы
своими координатами в некотором базисе
![]() (который
сам может быть явно и не определен).
Требуется найти матрицу
(который
сам может быть явно и не определен).
Требуется найти матрицу![]() перехода от
перехода от
![]() к
к
![]() .
.
Составляем матрицы
перехода от
![]() к
к![]() и
от
и
от
![]() к
к
![]() (по
столбцам координат векторов базисов
(по
столбцам координат векторов базисов
![]() и
и
![]() ).
Пусть это будут матрицы
).
Пусть это будут матрицы
![]() и
и
![]() соответственно. Тогда используя
утверждение 1.4, легко получим (см. рис.
1.2):
соответственно. Тогда используя
утверждение 1.4, легко получим (см. рис.
1.2):
![]()


![]()
A B

![]()
![]()
T
рис. 1.2
