
- •Глава 1. Элементы линейной алгебры
- •1.1. Понятие линейного пространства
- •Единственность нулевого вектора
- •Единственность противоположного вектора
- •Результат умножения на нуль
- •Результат умножения на
- •Результат умножения произвольного числа на нулевой вектор
- •1.2. Линейно зависимые и линейно независимые системы векторов. Базис и размерность.
- •1.3. Подпространства и линейные оболочки
- •1.4. Преобразования базисов
- •1.5. Вещественное евклидово пространство
- •1.6. Ортогональные системы векторов
- •1.7. Линейные операторы
- •1.8. Алгебра линейных операторов.
- •1.9. Матрица линейного оператора
- •1.10. Ортогональное дополнение
- •1.11. Собственные векторы и собственные числа линейного оператора.
- •1.12. Линейные формы
- •1.13. Билинейные и квадратичные формы
- •1.14. Сопряженный оператор. Самосопряженность
- •1.15. Ортогональные матрицы и ортогональные преобразования
- •1.16. Квадратичные формы в евклидовых пространствах. Закон инерции
- •1.17.Знакоопределенные квадратичные формы. Критерий Сильвестра.
- •1.18. Гиперповерхности второго порядка
- •1.19. Норма линейного оператора
1.15. Ортогональные матрицы и ортогональные преобразования
Определение 1.26 Квадратная невырожденная матрица называется ортогональной, если обратная к ней совпадает с транспонированной.
Роль ортогональных матриц в теории евклидовых пространств проясняет следующая теорема:
Теорема 1.15 Матрица ортогональна тогда и только тогда, когда она является матрицей перехода от одного ортонорма некоторого евклидова пространства к другому.
Доказательство.
Пусть
![]() - ортогональная матрица
- ортогональная матрица
![]() -ого
порядка. Докажем, что ее столбцы образуют
ортонормированный базис в
-ого
порядка. Докажем, что ее столбцы образуют
ортонормированный базис в
![]() .
.
Вычислим скалярное
произведение
![]() -ого
столбца на
-ого
столбца на
![]() -ый:
-ый:
![]() ,
,
так как
транспонированный
![]() -ый
столбец есть
-ый
столбец есть
![]() -ая
строка транспонированной матрицы,
совпадающей с обратной.
-ая
строка транспонированной матрицы,
совпадающей с обратной.
Рассматривая
столбцы матрицы
![]() как столбцы координат в каноническом
базисе, получим, что матрица
как столбцы координат в каноническом
базисе, получим, что матрица
![]() есть матрица перехода от одного ортонорма
(канонического базиса) в
есть матрица перехода от одного ортонорма
(канонического базиса) в
![]() к другому (состоящему из столбцов данной
матрицы).
к другому (состоящему из столбцов данной
матрицы).
Обратно, пусть
![]() и
и
![]() -
два ортонорма в
-
два ортонорма в
![]() -мерном
евклидовом пространстве, причем
-мерном
евклидовом пространстве, причем
![]() .
.
Вычислим матрицу
Грама для базиса
![]() (см.
п.1.6):
(см.
п.1.6):
![]() ,
,
так как матрица
Грама любого ортонорма единичная.
Отсюда, поскольку матрица
![]() ,
как матрица перехода, обратима,
,
как матрица перехода, обратима,
![]() .
.
Теорема доказана.
Определение 1.27 Линейный оператор, действующий в конечномерном евклидовом пространстве, называется ортогональным, если он задается (в каком-то ортонорме) ортогональной матрицей.
Таким образом, по
определению, оператор
![]() ортогонален, если в некотором ортонорме
ортогонален, если в некотором ортонорме
![]() он
задан ортогональной матрицей:
он
задан ортогональной матрицей:
![]() ,
,
где
![]() .
.
Легко доказать, что в любом ортонорме матрица ортогонального оператора ортогональна.
В самом деле, если
ортонорм
![]() ,
то поскольку матрица
,
то поскольку матрица
![]() ортогональна (теорема 1.15), то
ортогональна (теорема 1.15), то
![]()
Точно так же доказывается, что
![]()
Из доказанного сразу ( с учетом утверждения (6) теоремы 1.5 и следствия 1.4) вытекает:
Утверждение 1.21 Ортогональный оператор обратим, причем обратный к нему совпадает с сопряженным.
Теорема 1.16 Следующие условия равносильны:
-
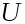 -
ортогональный оператор,
-
ортогональный оператор, -
для любых векторов
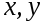

-
 .
.
Доказательство. Из условия (1) следует условие (3) (утверждение 1.21), а из этого последнего - условие (2):
![]()
Осталось доказать,
что из (2) следует (1). Для этого докажем,
что матрица![]() (в
произвольном ортонорме) оператора
(в
произвольном ортонорме) оператора
![]() ,
сохраняющего скалярное произведение,
обратима. Вычислим ядро оператора
,
сохраняющего скалярное произведение,
обратима. Вычислим ядро оператора
![]() .
Пусть для ненулевого вектора
.
Пусть для ненулевого вектора
![]()
![]() .
Тогда
.
Тогда
![]() ,
что невозможно. Итак,
,
что невозможно. Итак,
![]() ,
т.е. из
,
т.е. из
![]() следует
следует
![]() .
Это значит,
что система
.
Это значит,
что система
![]() имеет только нулевое решение, откуда
(первый семестр!)
имеет только нулевое решение, откуда
(первый семестр!)
![]() ,
т.е. матрица
,
т.е. матрица
![]() обратима. Тогда
из условия сохранения скалярного
произведения получим:
обратима. Тогда
из условия сохранения скалярного
произведения получим:
![]()
Так как это имеет
место для любых векторов
![]() ,
то
,
то
![]() ,
а так как матрица
,
а так как матрица
![]() обратима, то
обратима, то
![]() ,
и оператор
,
и оператор
![]() является ортогональным.
является ортогональным.
Теорема доказана.
Замечание.
Доказав тривиальность ядра оператора
![]() ,
мы могли бы также сослаться на утверждение
1.7, замечания, сделанные в конце п. 1.8, и
на утверждение (6) теоремы 1.5.
,
мы могли бы также сослаться на утверждение
1.7, замечания, сделанные в конце п. 1.8, и
на утверждение (6) теоремы 1.5.
В силу этой теоремы можно ортогональный оператор определить как оператор, сохраняющий скалярное произведение, или как оператор, у которого обратный совпадает с сопряженным.
Отсюда, в частности, следует, что самосопряженный ортогональный оператор обратен себе самому.
Ортогональные операторы (их называют также ортогональными преобразованиями) играют в линейной алгебре и ее приложениях очень важную роль. В заключение этого пункта мы дадим характеристику всех ортогональных матриц второго порядка.
Пусть матрица
![]()
ортогональна. Тогда должно выполняться:
![]()
![]()
Первая строчка из написанных трех следует из того, что столбцы ортогональной матрицы ортонормированны; вторая и третья - из условия равенства обратной и транспонированной матриц.
Из первых двух строк получаем:
![]()
1 случай:
![]() .
.
![]()
При
![]() получаем матрицу
получаем матрицу
![]() ,
,
причем
![]() ,
т.е., вся совокупность матриц в этом
случае описывается так:
,
т.е., вся совокупность матриц в этом
случае описывается так:
![]() (1)
(1)
Если же
![]() ,
то поскольку
,
то поскольку
![]() ,
мы можем положить
,
мы можем положить
![]()
для некоторого
![]() .
.
Матрица
![]() может быть тогда записана в виде:
может быть тогда записана в виде:
![]() (2)
(2)
2 случай:
![]() .
.
![]()
При
![]() получаем снова матрицу вида (1).
получаем снова матрицу вида (1).
При
![]() аналогично предыдущему придем к матрице:
аналогично предыдущему придем к матрице:
![]() (3)
(3)
Остановимся на геометрической интерпретации выведенных матриц.
Матрица вида (1) есть либо матрица тождественного преобразования плоскости (точнее, множества геометрических векторов, лежащих в некоторой плоскости), либо «отражения» одной из осей, либо одновременного отражения обеих осей - поворота на 180).
Матрица вида (2)
есть матрица поворота на угол
![]() с последующим отражением одной из осей.
с последующим отражением одной из осей.
Матрица (3) есть
классическая матрица поворота на угол
![]() .
Обратная к ней матрица
.
Обратная к ней матрица
![]()
есть, естественно,
матрица поворота на угол
![]() .
.
В частности, если
![]() ,
то матрица
,
то матрица
![]()
является обратной к себе самой.
