
Избранные задачи
-
Пусть последовательность {
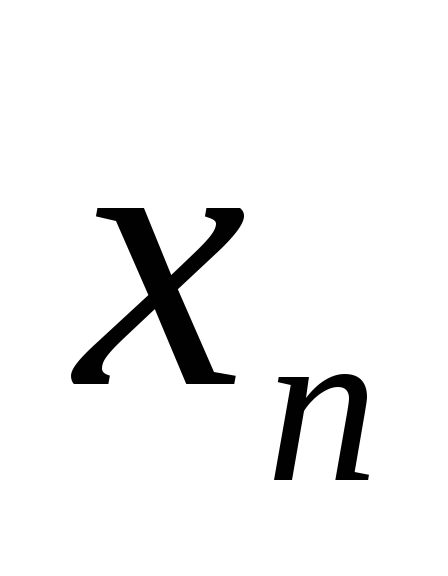 }
сходится и ее предел a>0.
Можно ли из {
}
сходится и ее предел a>0.
Можно ли из {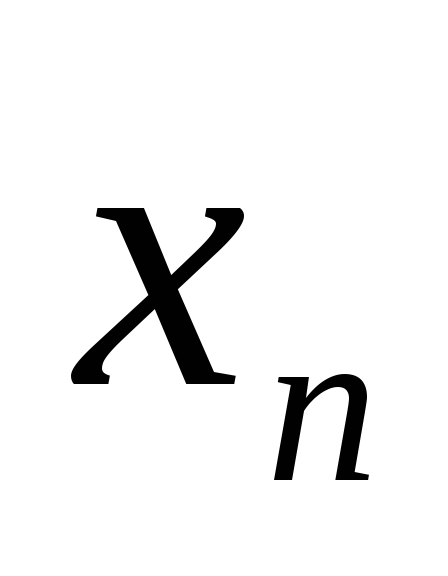 }
выделить подпоследовательность, все
члены которой отрицательны? (не
положительны?).
}
выделить подпоследовательность, все
члены которой отрицательны? (не
положительны?). -
Пусть в некоторой окрестности точки a лежит бесконечно много членов последовательности {
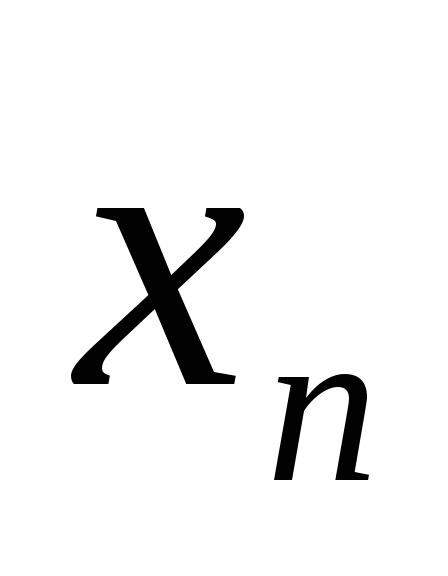 }.
Следует ли отсюда, что а является
пределом последовательности {
}.
Следует ли отсюда, что а является
пределом последовательности {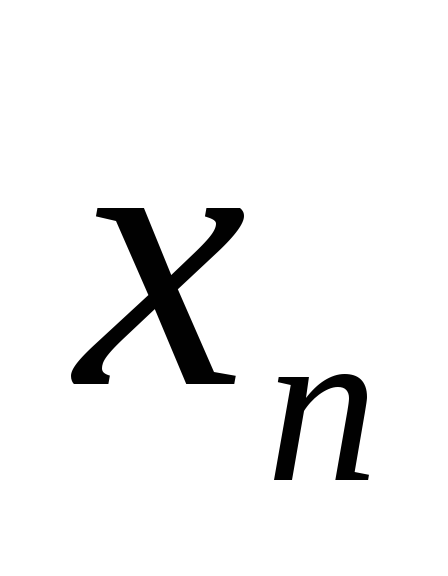 }?
(Что никакая точка вне этой окрестности
не является пределом последовательности
{
}?
(Что никакая точка вне этой окрестности
не является пределом последовательности
{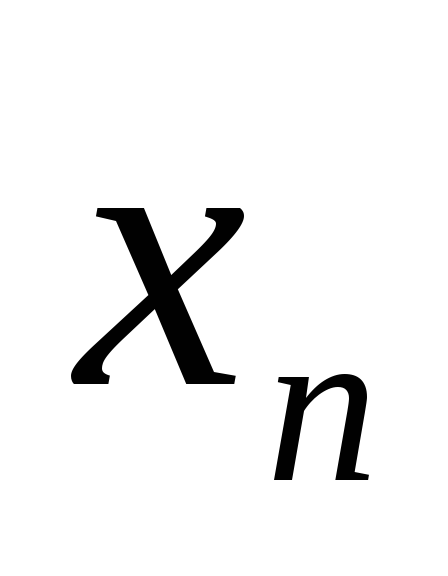 }?).
}?). -
Пусть в любой окрестности точки а лежит бесконечно много членов последовательности {
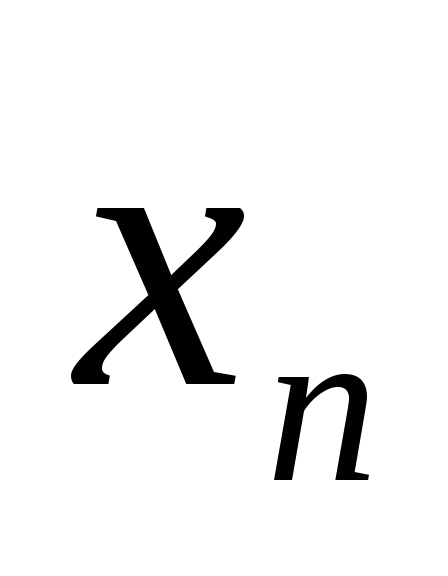 }.
Следует ли отсюда, что а является
пределом последовательности {
}.
Следует ли отсюда, что а является
пределом последовательности {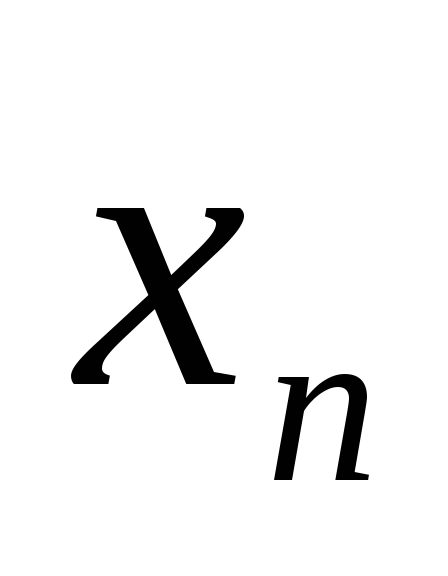 }?
(Что последовательность {
}?
(Что последовательность {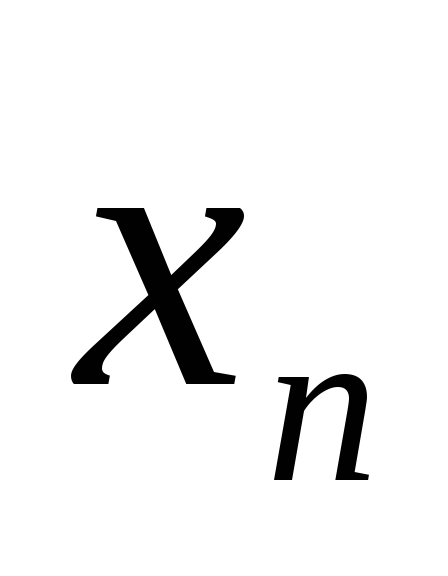 }
является ограниченной?)
}
является ограниченной?) -
Пусть последовательность {|
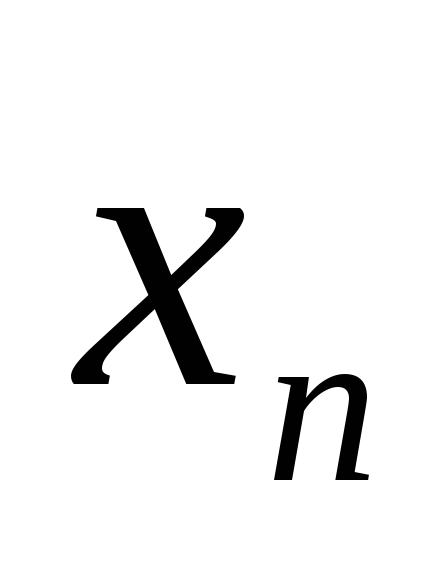 |}
сходится. Будет ли из этого вытекать,
что последовательность {
|}
сходится. Будет ли из этого вытекать,
что последовательность {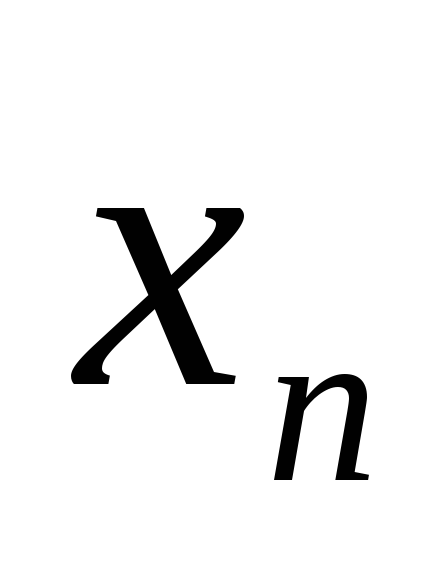 }
будет сходящейся? (Будет ли из этого
вытекать, что последовательность {
}
будет сходящейся? (Будет ли из этого
вытекать, что последовательность {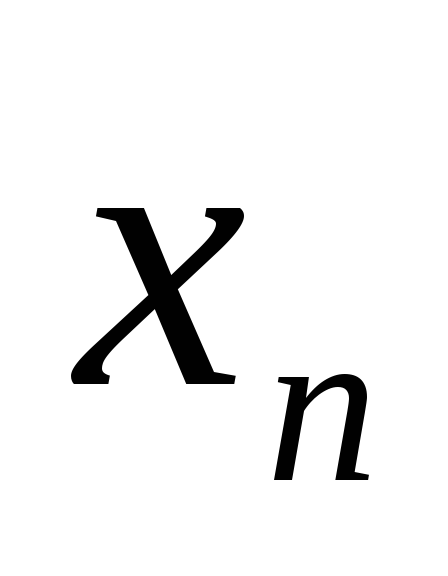 }
будет ограниченной?)
}
будет ограниченной?) -
Пусть последовательность {
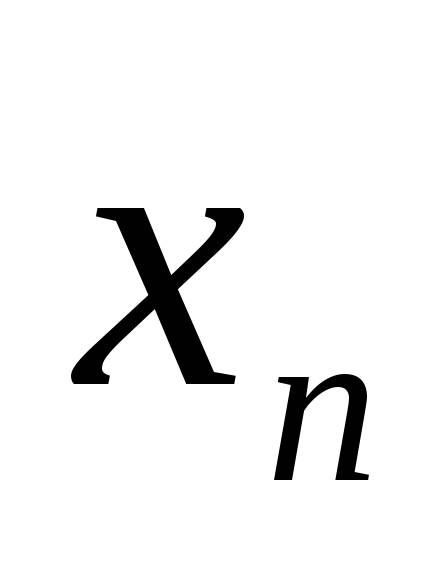 }
сходится и М=sup{
}
сходится и М=sup{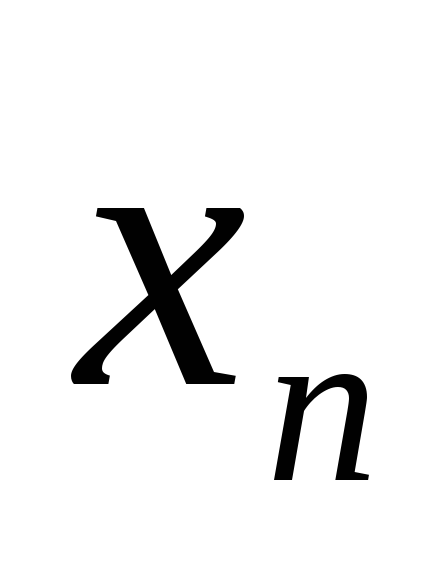 },
m=inf{
},
m=inf{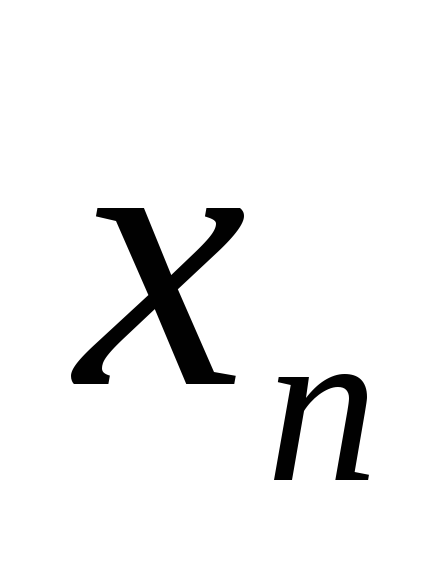 }.
Докажите, что: либо
}.
Докажите, что: либо
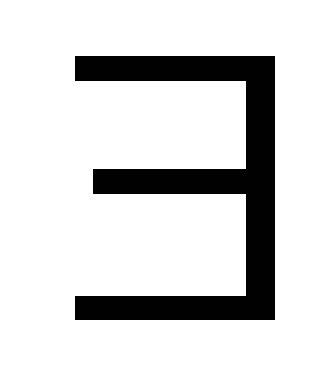 n такое, что
n такое, что
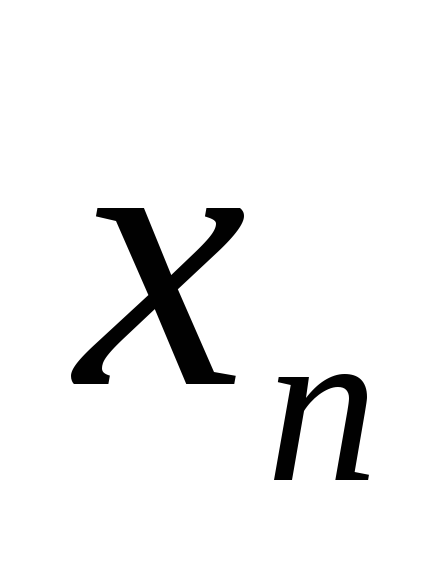 =M;
либо
=M;
либо
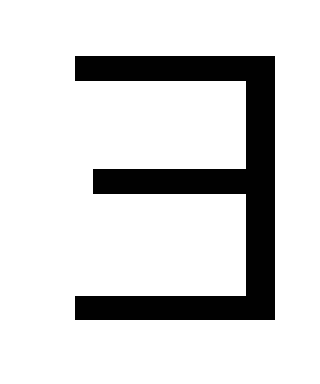 k такое, что
k такое, что
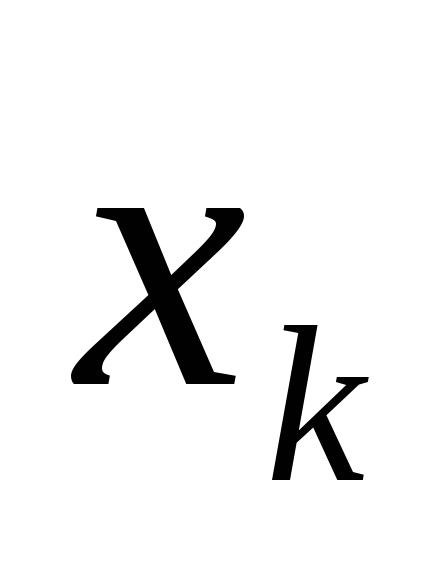 =m;
либо
=m;
либо
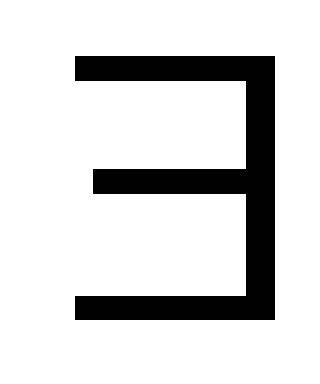 n,k такие,
что
n,k такие,
что
 =M,
=M,
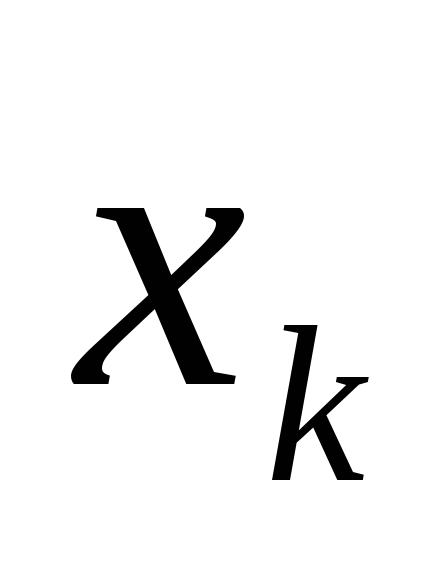 =m.
=m. -
Является ли любая неограниченная последовательность бесконечно большой?
-
Известно, что в некоторой окрестности нуля находится бесконечное число членов последовательности. Следует ли отсюда, что последовательность является бесконечно малой? (бесконечно большой? ограниченной?)
-
Пусть последовательность {
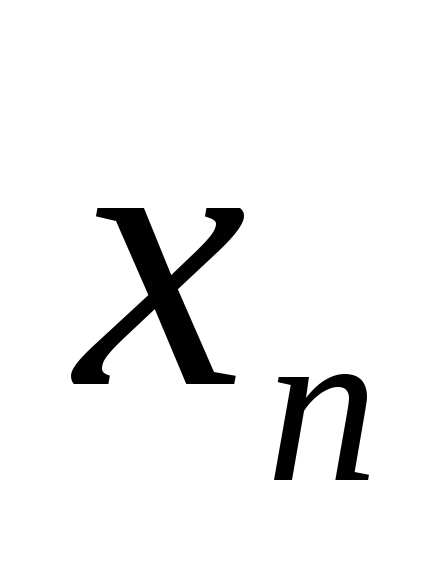 }
сходится, а {
}
сходится, а {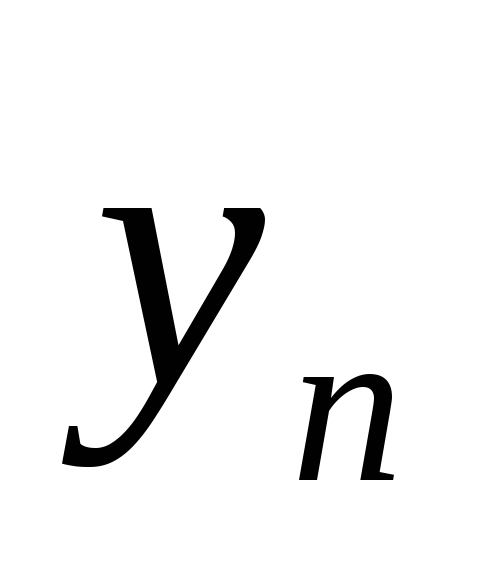 }
расходится. Докажите, что {c
}
расходится. Докажите, что {c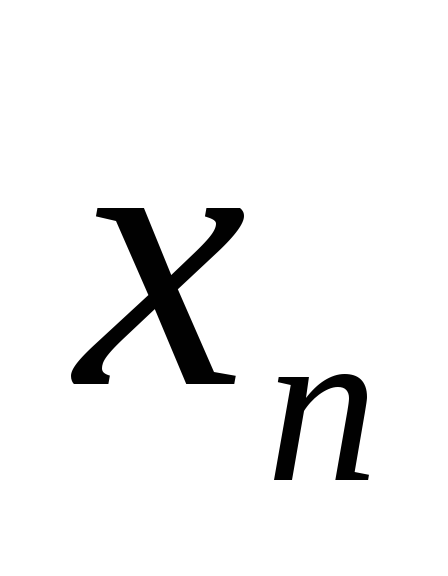 }
сходится при любом c,
{
}
сходится при любом c,
{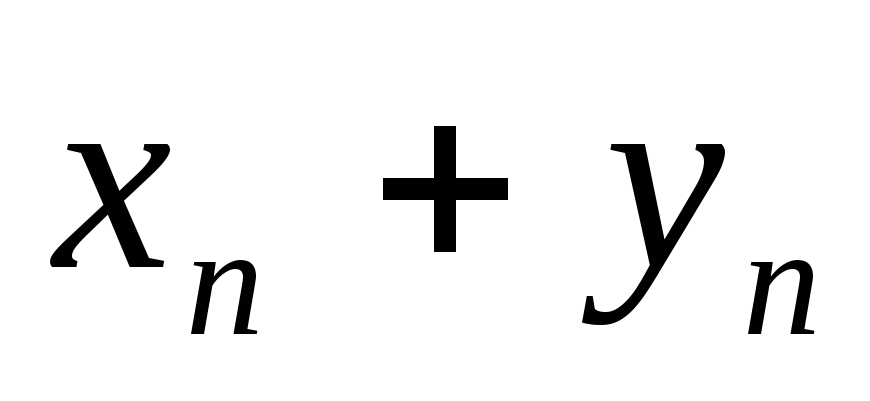 },
},
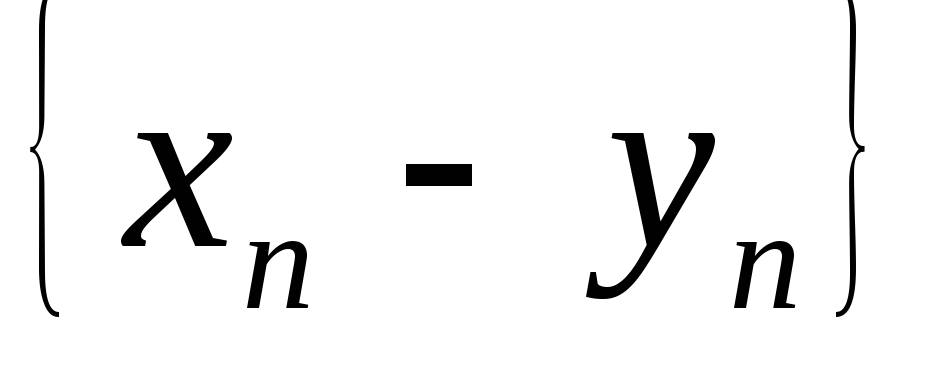 расходятся. Постройте примеры,
показывающие, что последовательность
{
расходятся. Постройте примеры,
показывающие, что последовательность
{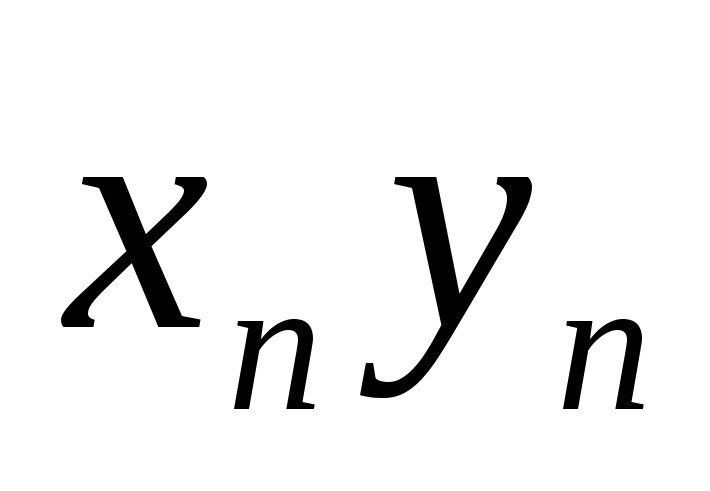 }
может быть как сходящейся, так и
расходящейся.
}
может быть как сходящейся, так и
расходящейся. -
Покажите, что для того чтобы монотонно возрастающая последовательность сходилась необходимо и достаточно, чтобы она была ограничена сверху.
-
Покажите, что для того чтобы монотонно убывающая последовательность сходилась необходимо и достаточно, чтобы она была ограничена снизу.
-
Верно ли утверждение “Если последовательность неограниченна, то из нее нельзя выделить сходящуюся подпоследовательность”?
-
Покажите, что из любой неограниченной последовательности можно выделить бесконечно большую подпоследовательность.
-
Покажите, что если монотонная последовательность является неограниченной, то из нее нельзя выделить сходящуюся подпоследовательность.
-
Пусть последовательность {
 }
такова, что её подпоследовательности
}
такова, что её подпоследовательности
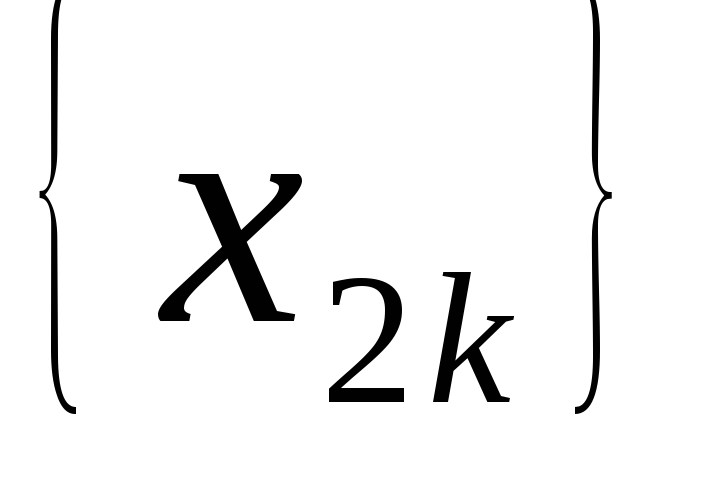 ,
,
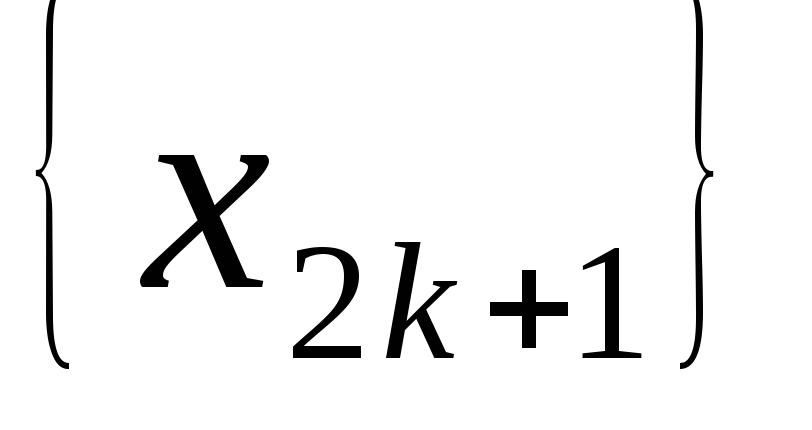 ,
,
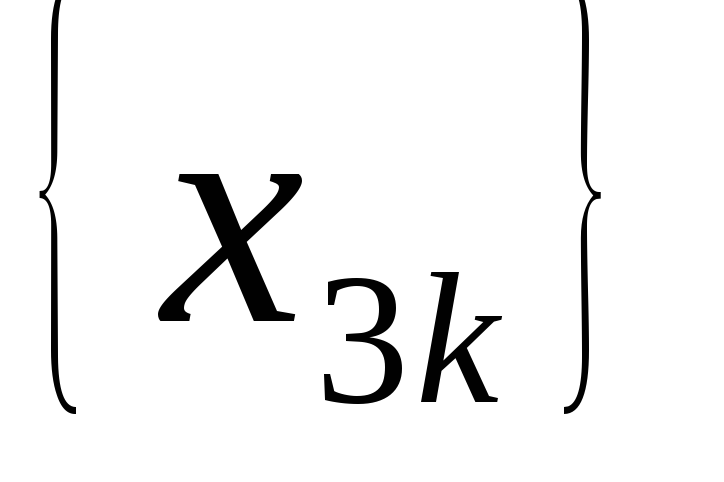 сходятся. Покажите, что тогда сама
последовательность {
сходятся. Покажите, что тогда сама
последовательность {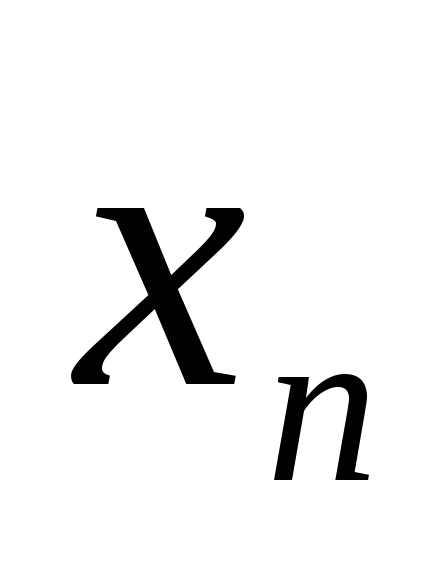 }
будет сходящейся.
}
будет сходящейся. -
Пусть
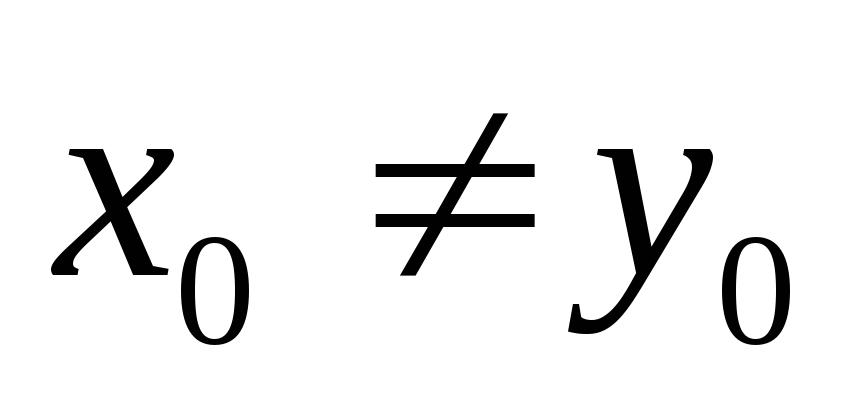 ,
постройте такую последовательность
{
,
постройте такую последовательность
{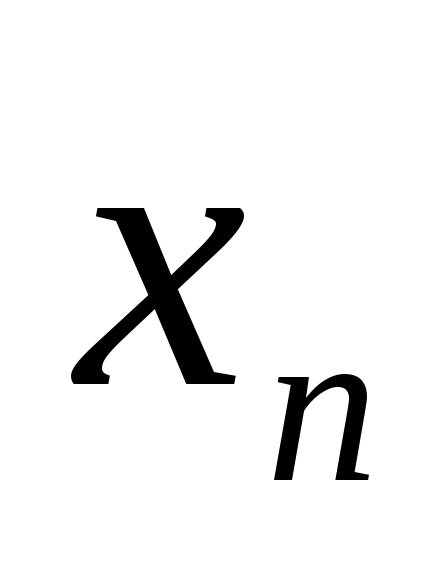 },
из которой можно выделить две
подпоследовательности
},
из которой можно выделить две
подпоследовательности
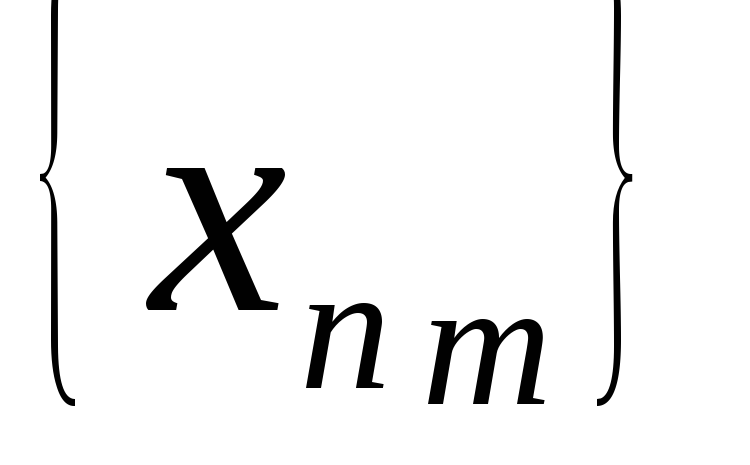 и
и
 ,
одна из которых сходится к
,
одна из которых сходится к
 ,
а вторая - к
,
а вторая - к
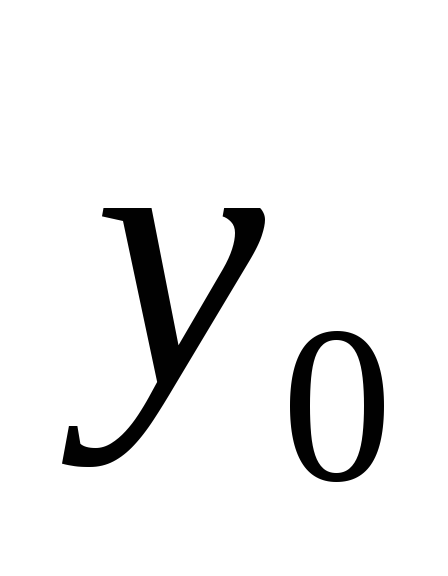 .
. -
Постройте такую последовательность {
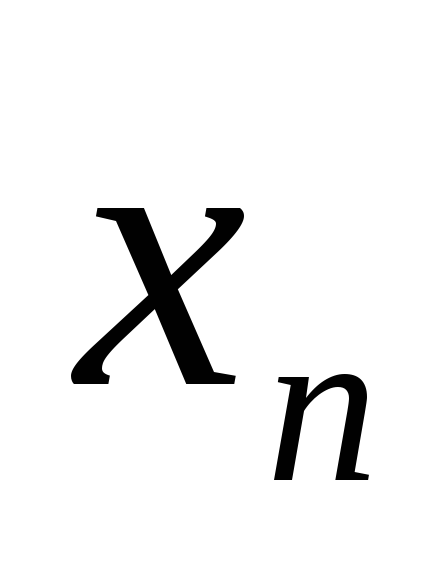 },
из которой для любого рационального
числа r можно выделить
подпоследовательность
},
из которой для любого рационального
числа r можно выделить
подпоследовательность
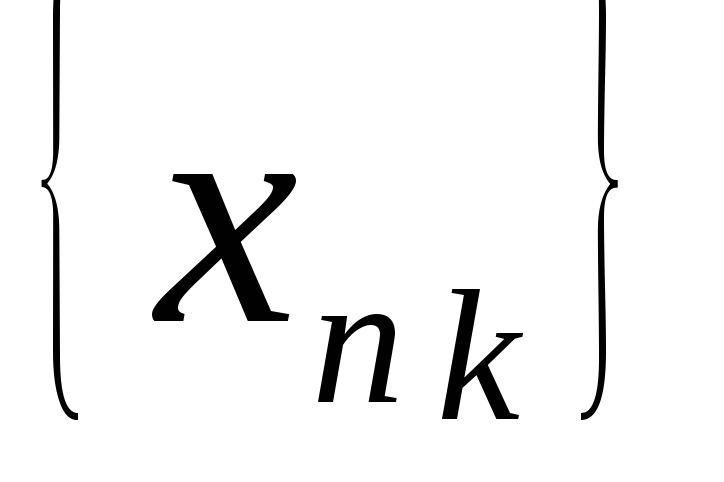 ,
сходящуюся к r.
,
сходящуюся к r. -
Будет ли последовательность, удовлетворяющая условиям задачи 2, ограниченной?
-
Можно ли построить такую последовательность {
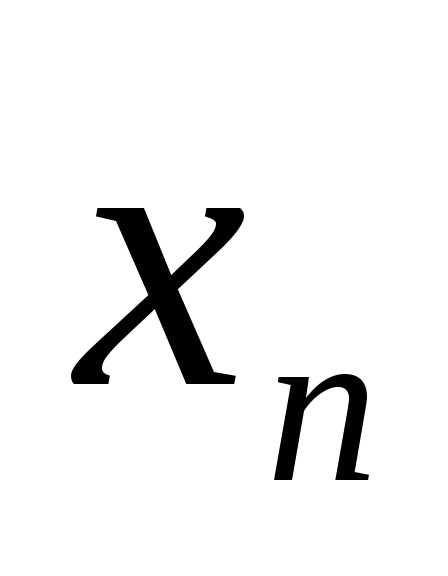 },
из которой для любого действительного
числа а можно выделить
подпоследовательность
},
из которой для любого действительного
числа а можно выделить
подпоследовательность
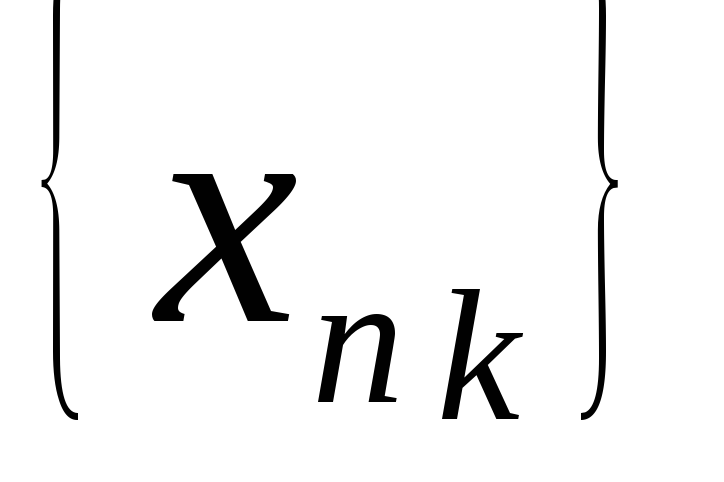 ,
сходящуюся к а?
,
сходящуюся к а? -
Покажите, что из любой ограниченной последовательности {
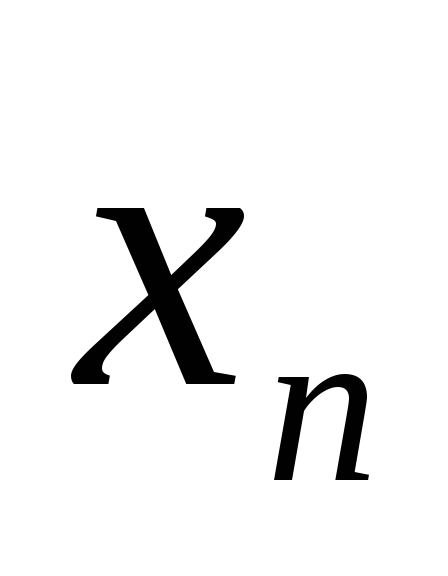 }
можно выделить сходящуюся
подпоследовательность.
}
можно выделить сходящуюся
подпоследовательность. -
Верно ли утверждение ‘Пусть при всех n
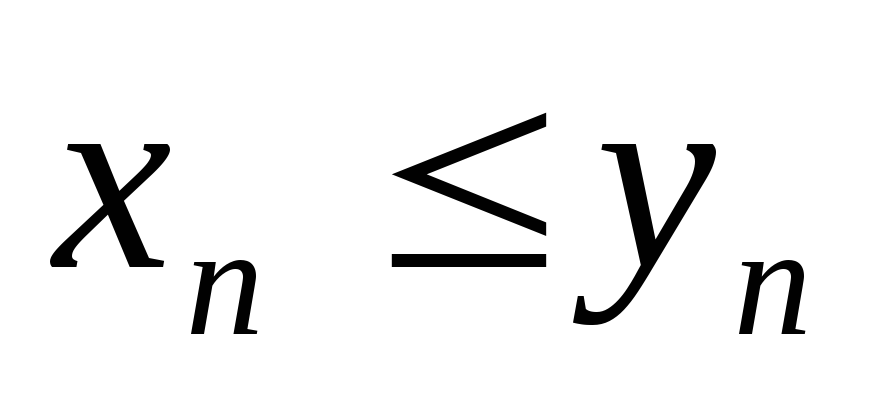 и последовательности {
и последовательности {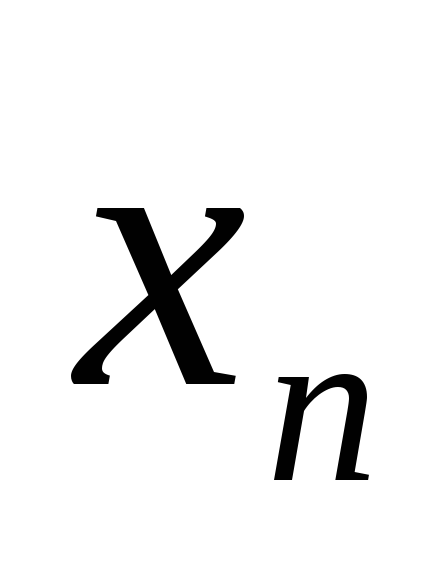 }
и {
}
и {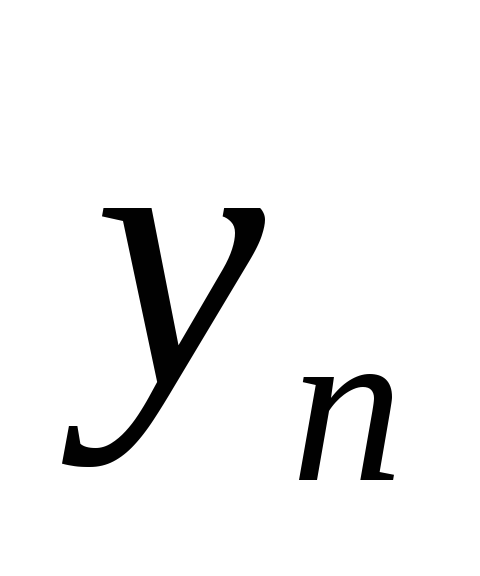 }
ограничены. Тогда, каковы бы ни были
сходящиеся последовательности
}
ограничены. Тогда, каковы бы ни были
сходящиеся последовательности
 и
и
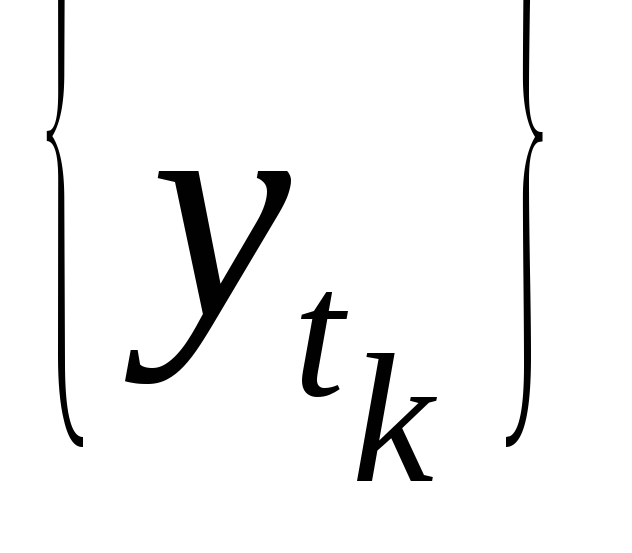
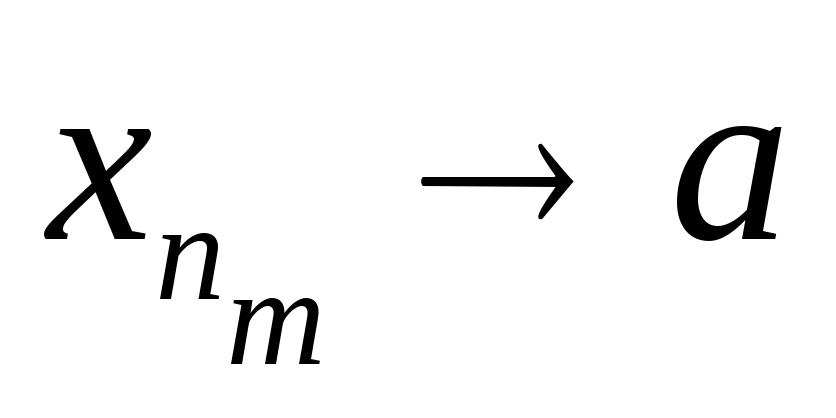
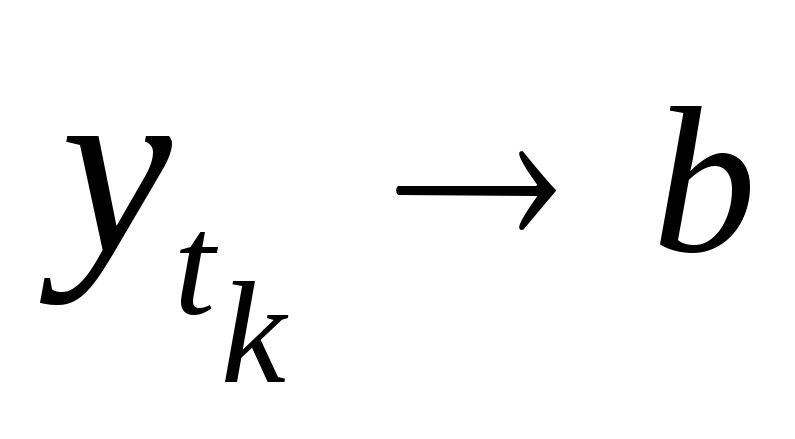 ,
то
,
то
 ”?
”? -
Существует ли такая последовательность {
 },
что из любой её подпоследовательности
},
что из любой её подпоследовательности
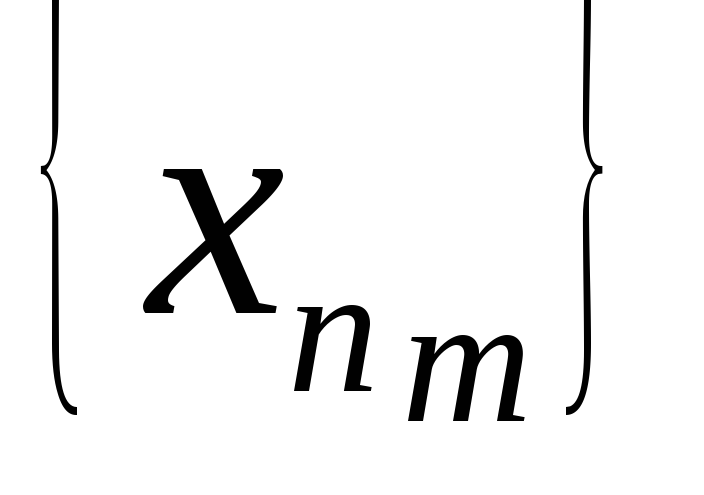 можно выделить сходящуюся частичную
подпоследовательность
можно выделить сходящуюся частичную
подпоследовательность
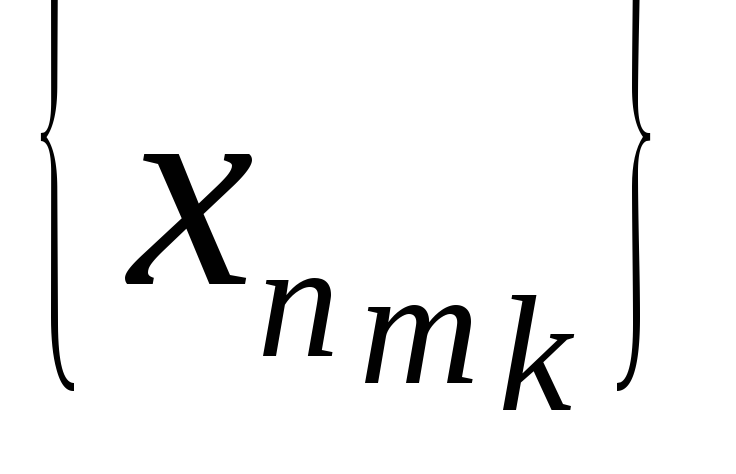 ?
? -
Существует ли такая последовательность {
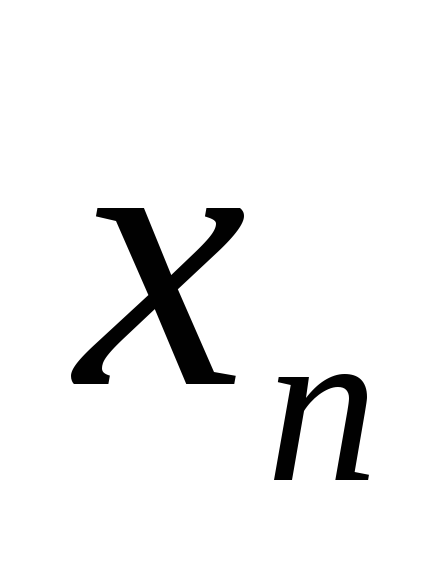 },
что из любой её подпоследовательности
},
что из любой её подпоследовательности
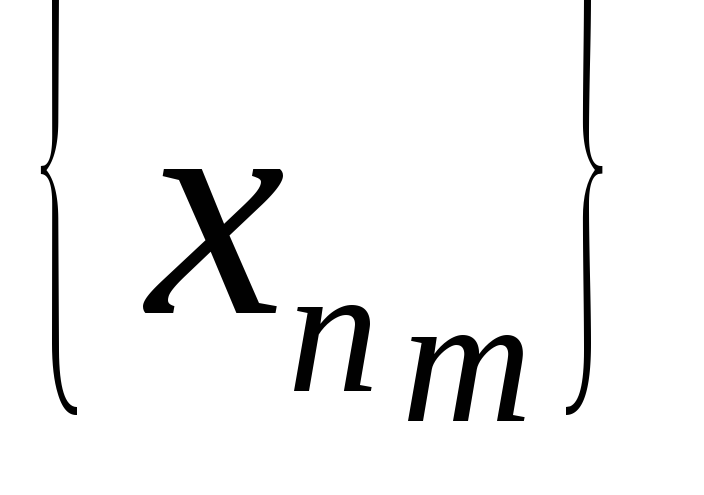 можно выделить неограниченную частичную
подпоследовательность
можно выделить неограниченную частичную
подпоследовательность
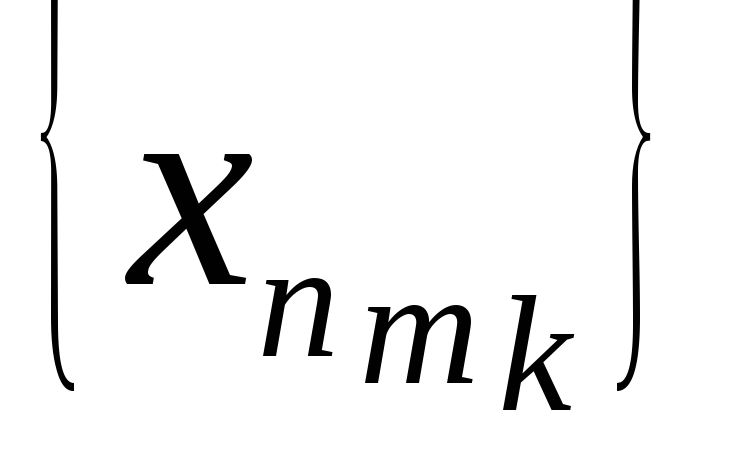 ?
? -
Существует ли такая последовательность {
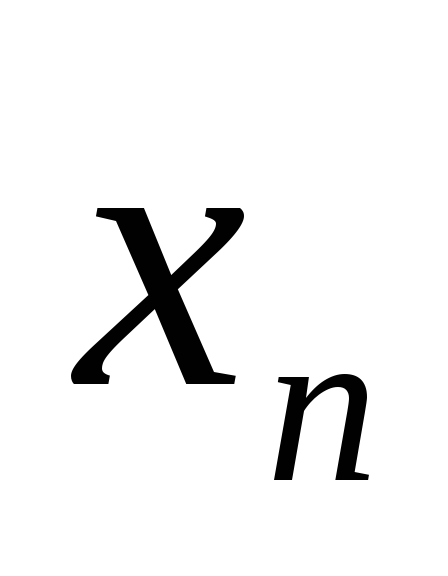 },
что из любой её подпоследовательности
},
что из любой её подпоследовательности
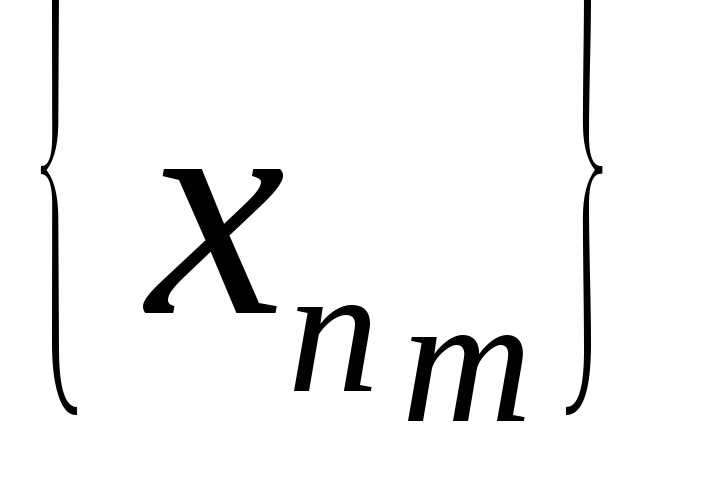 можно выделить как сходящуюся частичную
подпоследовательность так и неограниченную
частичную подпоследовательность?
можно выделить как сходящуюся частичную
подпоследовательность так и неограниченную
частичную подпоследовательность? -
Пусть из любой подпоследовательности
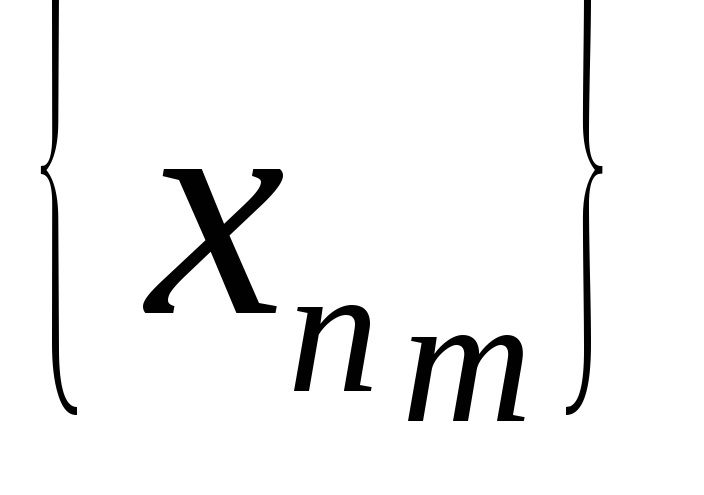 последовательности {
последовательности {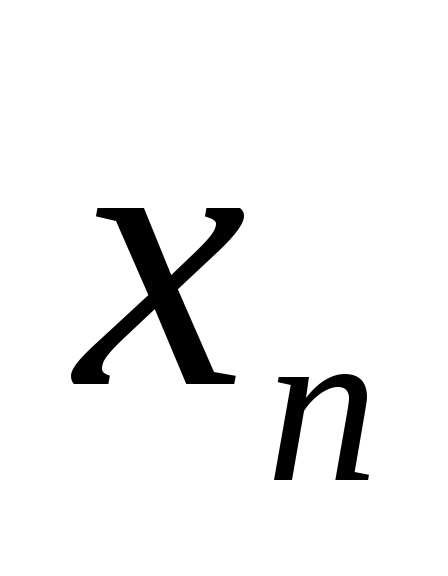 }
можно выделить сходящуюся частичную
подпоследовательность
}
можно выделить сходящуюся частичную
подпоследовательность
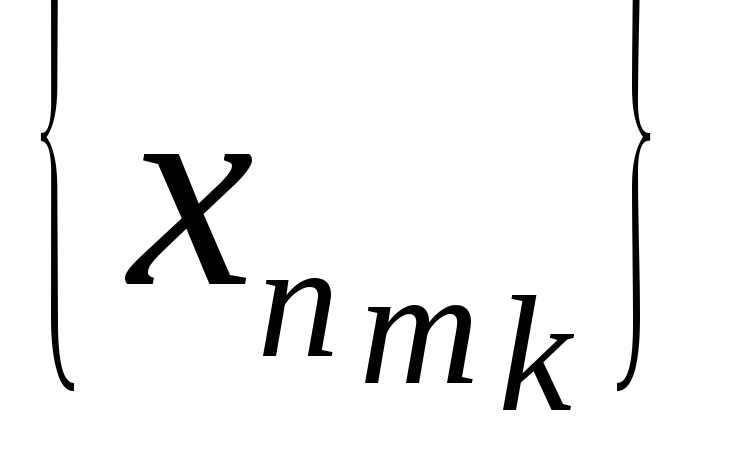 .
Покажите, что исходная последовательность
{
.
Покажите, что исходная последовательность
{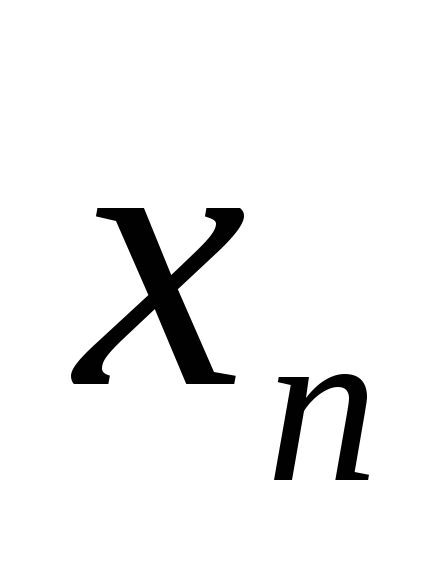 }
будет ограниченной.
}
будет ограниченной. -
Пусть из любой подпоследовательности
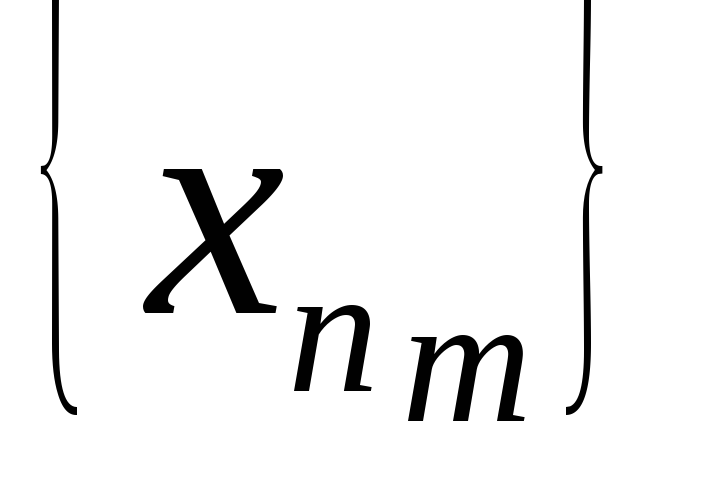 последовательности {
последовательности {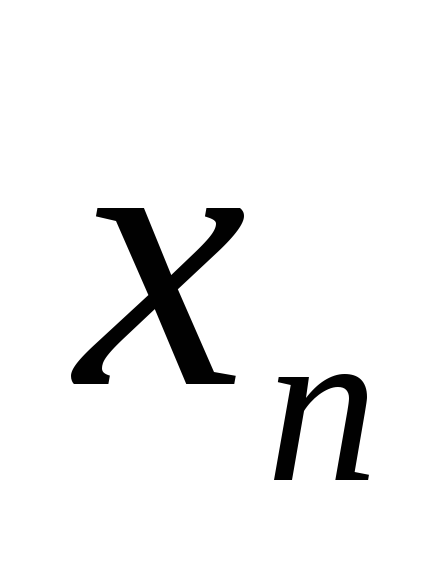 }
можно выделить частичную подпоследовательность
}
можно выделить частичную подпоследовательность
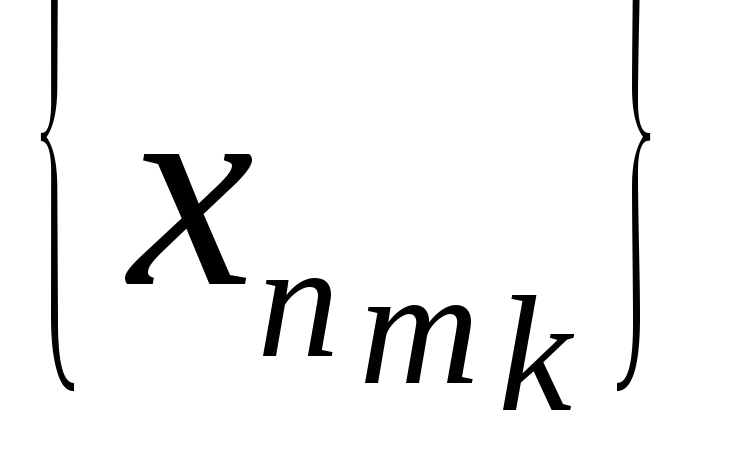 ,
сходящуюся к
,
сходящуюся к
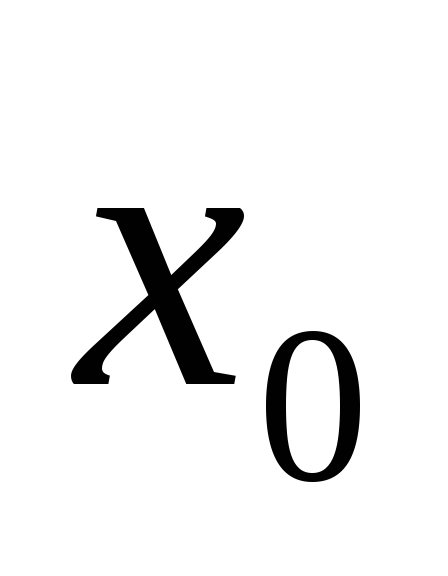 .
Покажите, что исходная последовательность
{
.
Покажите, что исходная последовательность
{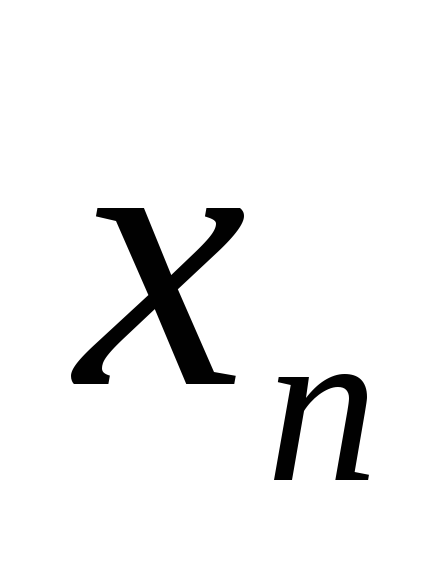 }
будет сходиться к
}
будет сходиться к
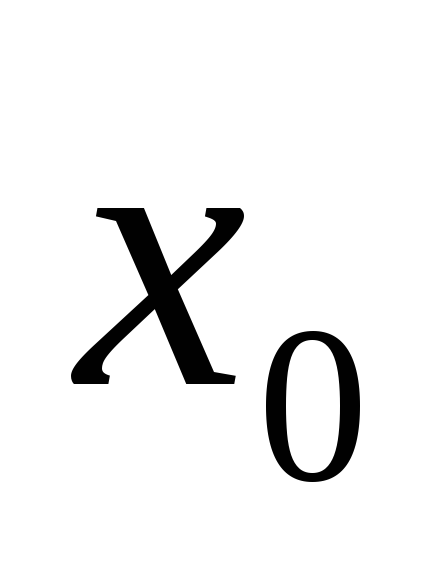 .
. -
Для того чтобы последовательность {
 }
сходилась к
}
сходилась к
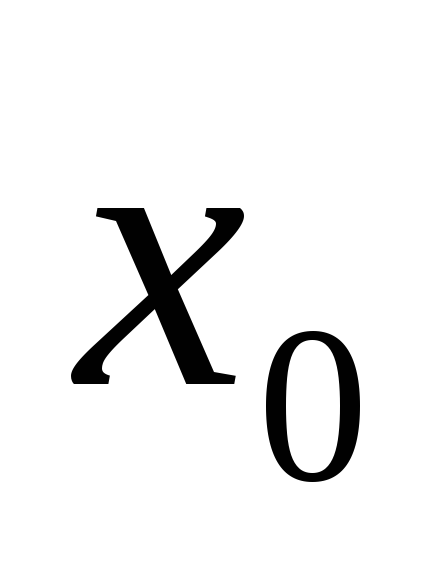 необходимо и достаточно, чтобы из любой
подпоследовательности
необходимо и достаточно, чтобы из любой
подпоследовательности
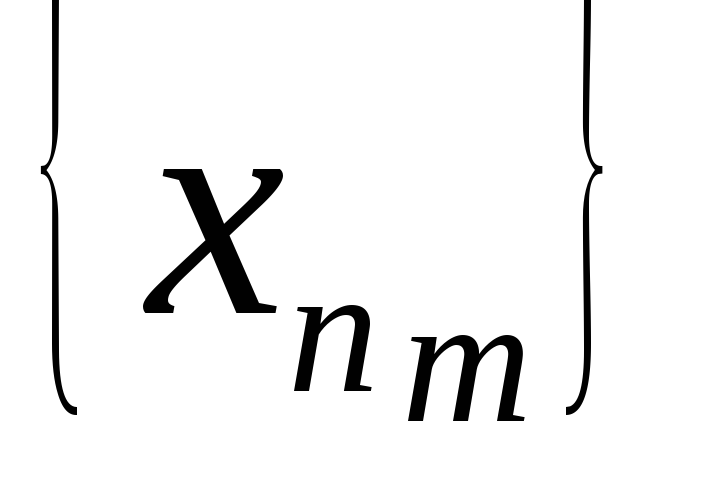 последовательности {
последовательности {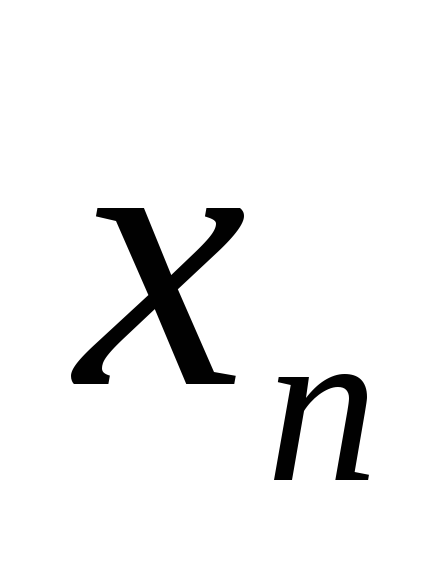 }
можно выделить частичную подпоследовательность
}
можно выделить частичную подпоследовательность
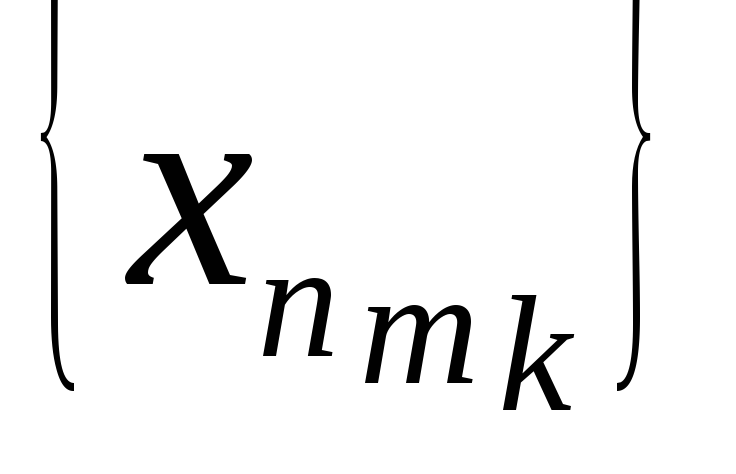 ,
сходящуюся к
,
сходящуюся к
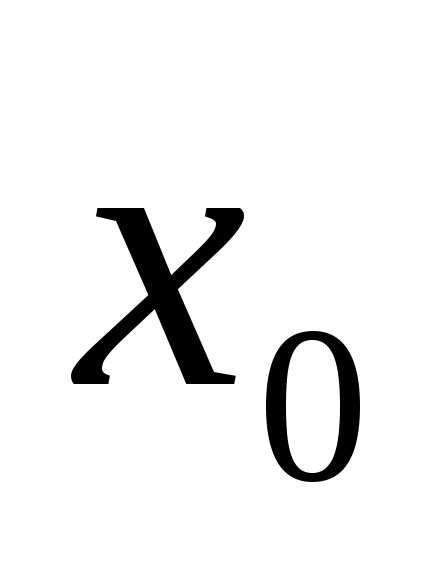 .
. -
Из сходящейся последовательности {
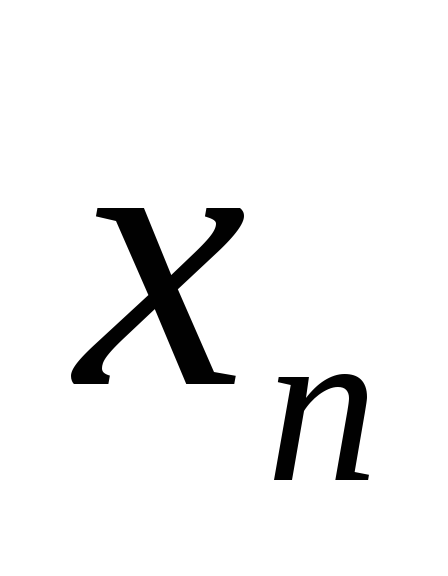 }
}
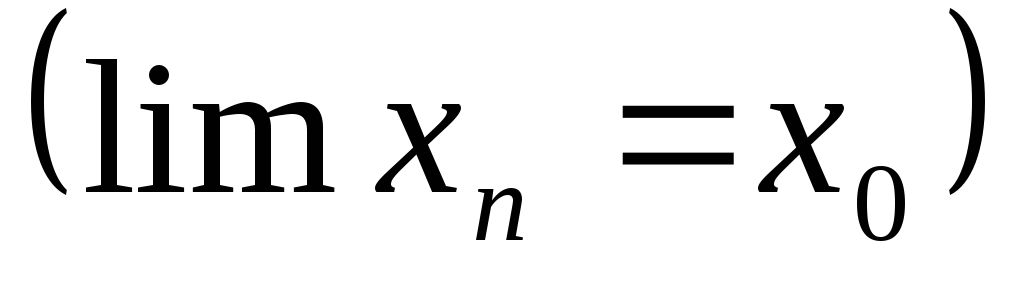 произвольным образом выбираем бесконечное
число членов {
произвольным образом выбираем бесконечное
число членов {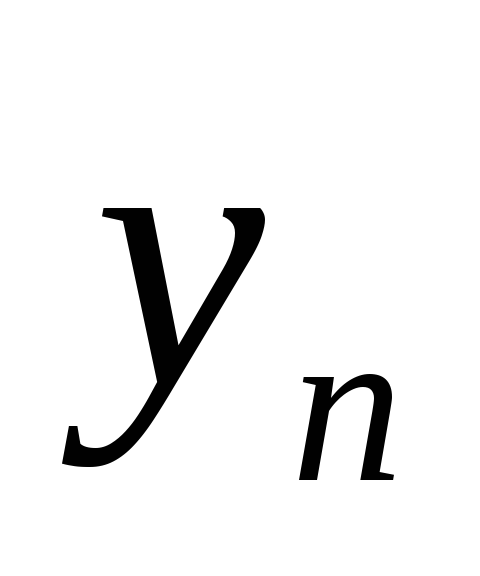 }
Покажите, что из любой подпоследовательности
}
Покажите, что из любой подпоследовательности
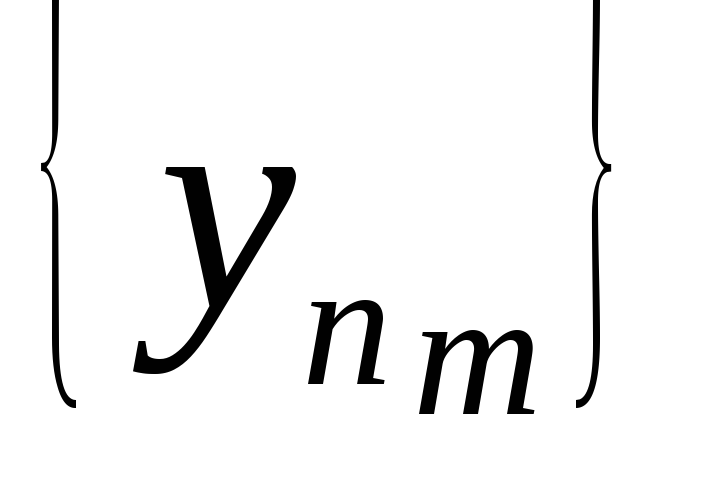 последовательности {
последовательности {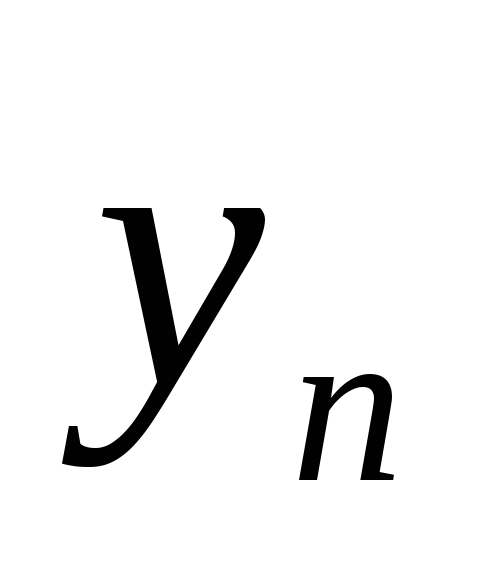 }
можно выделить частичную последовательность
}
можно выделить частичную последовательность
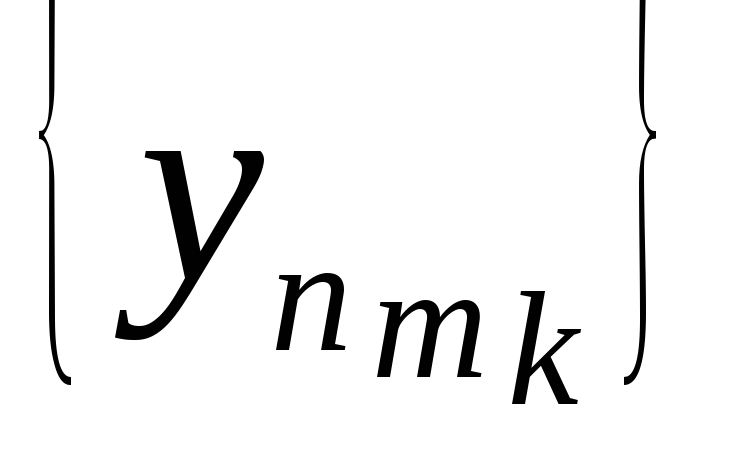 ,
сходящуюся к
,
сходящуюся к
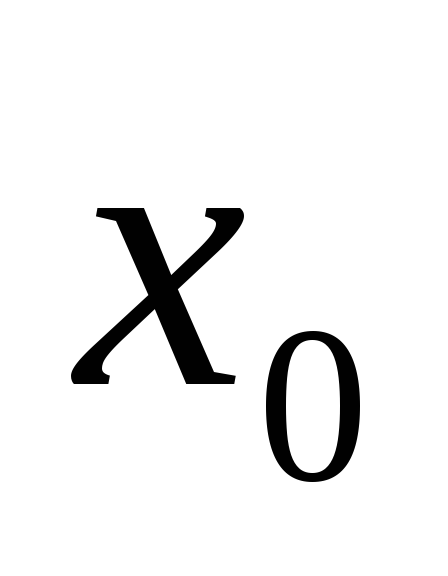 .
. -
Из сходящейся последовательности {
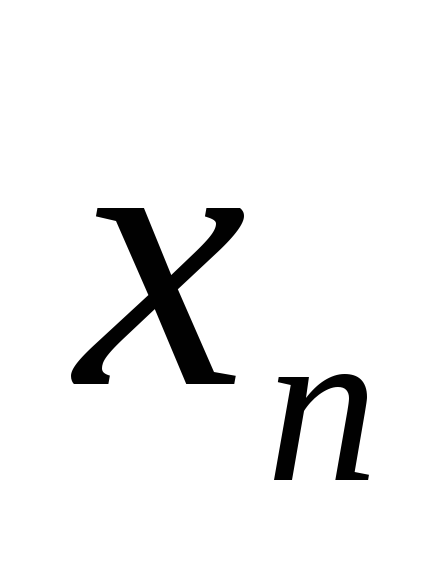 }
}
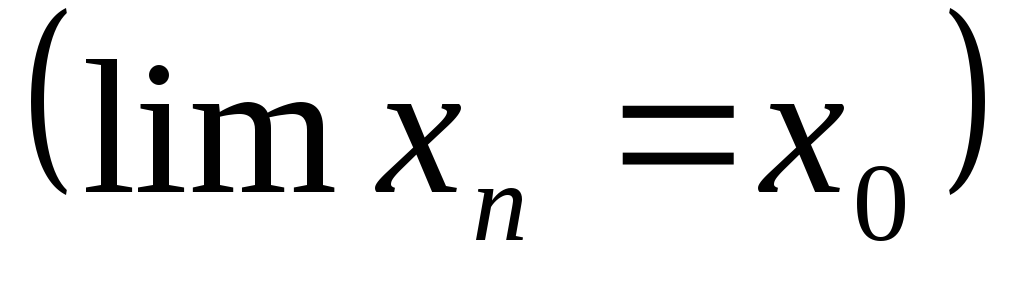 произвольным образом выбираем бесконечное
число членов {
произвольным образом выбираем бесконечное
число членов {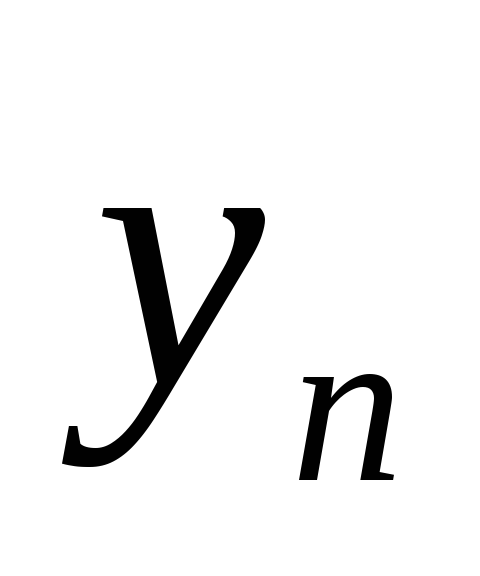 }
Покажите, что последовательность {
}
Покажите, что последовательность {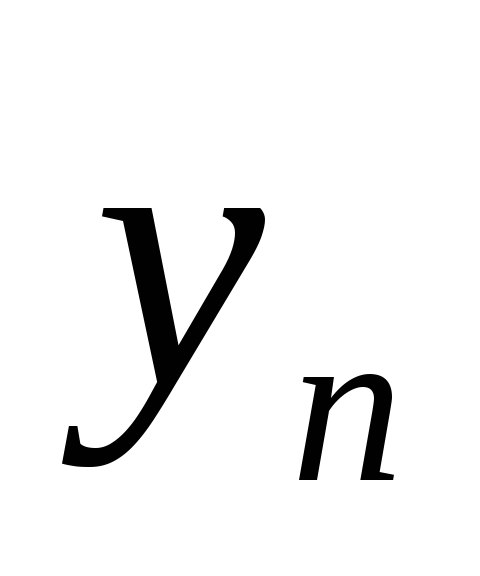 }
сходится. Найдите предел этой
последовательности.
}
сходится. Найдите предел этой
последовательности.
