Федеральное агентство по образованию
Воронежский государственный университет
Математический анализ
Числовые последовательности.
Предел числовой последовательности
Учебно-методическое пособие
по специальности 071900 «Информационные системы и технологии»
для студентов 1 курса очной формы обучения
(издание второе переработанное и дополненное)
Воронеж - 2008
Аннотация издания
Пособие является переработанным и дополненным изданием выпущенного в 2006 году одноименного учебно-методического пособия, созданного на основе опыта преподавания курса математического анализа на факультете компьютерных наук ВГУ. В него включен материал, относящийся к темам «Числовые последовательности» и «Предел числовой последовательности». Каждый параграф содержит справочный материал, набор типовых примеров с решениями и задачи для самостоятельной работы. В пособии приведены варианты заданий, предлагавшихся на второй рубежной аттестации аттестации.
Рекомендовано научно-методическим советом математического факультета ВГУ
Авторы: к.ф-м.н, доцент Сергей Анатольевич Скляднев;
ассистент Светлана Вячеславовна Писарева
Научный редактор: д.ф-м.н, профессор Владимир Алексеевич Костин
Рецензент: д.ф-м.н, профессор Александр Васильевич Лобода
Редактор: О.А. Тихомирова
С.А. Скляднев, С.В. Писарева
Воронежский государственный университет
§ 1. Числовые последовательности
СПРАВОЧНЫЕ СВЕДЕНИЯ
1.1 Определение числовой последовательности
Если каждому числу n из
натурального ряда чисел 1, 2, 3, ...,
,
... поставлено в соответствие вещественное
число
,
то множество вещественных чисел
называется
числовой последовательностью или просто
последовательностью.
Числа
называются элементами (членами)
последовательности, символ
— общим элементом (членом) последовательности,
а
— номером элемента. Последовательность,
как правило, обозначают символом
.
Последовательности
,
,
,
называются соответственно суммой,
разностью, произведением и частным двух
последовательностей:
и
.
Множество значений последовательности
может быть как конечным, так и бесконечным,
например, множество значений
последовательности
состоит из двух чисел, 1 и -1, множество
значений последовательности
бесконечно. Последовательность, множество
значений которой состоит из одного
числа, называют стационарной.
Последовательность может быть задана с помощью формулы вида
.
Формулу, выражающую
через номер
,
например,
;
;
называют формулой общего члена последовательности.
Для задания последовательности используют
и рекуррентные формулы, т.е. формулы,
выражающие
-й
член последовательности через члены с
меньшими номерами (предшествующие
члены). Так определяют арифметическую
и геометрическую прогрессии. Другими
примерами являются последовательности
,
,
,
где a, b, c - заданные числа.
Последовательность
называют подпоследовательностью
последовательности
,
если есть такая строго возрастающая
последовательность номеров
,
что для любого
.
1.2 Ограниченные последовательности
Последовательность
ограничена снизу, если существует число
такое, что для всех
верно неравенство
.
Число
называют нижней гранью последовательности.
Последовательность
ограничена сверху, если существует
число
такое, что для всех
верно неравенство
.
Число
называют верхней гранью последовательности.
Последовательность
ограничена, если существуют числа
и
такие, что для всех
верны неравенства
.
Это определение равносильно следующему:
последовательность
ограничена, если существует число
такое, что для всех
верно неравенство
,
или
:
.
Следовательно, последовательность ограничена тогда и только тогда, когда ограничено множество ее значений.
Последовательность
не ограничена, если для любого
найдется
такое, что верно неравенство
;
или
:
.
Аналогично формулируется определение неограниченной сверху (снизу) последовательности.
1.3 Точные грани последовательностей
Число m называют точной
нижней гранью (или инфимумом) множества
членов последовательности
(записывают
),
если:
1).
;
2).
:
.
Число M называют точной
верхней гранью (или супремумом) множества
членов последовательности
(записывают
),
если:
1)
;
2)
:
.
Член
последовательности
называют наибольшим (соответственно
наименьшим), если
(соответственно
)
для любого
,
и обозначают его
(соответственно
).
Наибольший (соответственно наименьший) член последовательности называют также максимальным (соответственно минимальным).
Если существует
(соответственно
),
то
=
(соответственно
=
).
Из существования
(соответственно
)
не следует существования
(соответственно
).
1.4 Монотонные последовательности
Последовательность
называют возрастающей (неубывающей),
начиная с номера
,
если для любого
,
,
верно неравенство
.
Последовательность
называют убывающей (невозрастающей),
начиная с номера
,
если для любого
,
,
верно неравенство
.
Невозрастающую или неубывающую, начиная
с номера
,
последовательность называют монотонной,
начиная с номера
(возрастающую или убывающую — строго
монотонной).
Последовательность, возрастающую с
номера
,
называют возрастающей (аналогично,
убывающей и т. д.).
ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Дана
формула общего члена последовательности
:
.
Написать пять первых членов этой последовательности.
Решение. Подставляя последовательно
значения
=1,
2, 3, 4, 5 в данную формулу общего члена
последовательности, получаем:
;
;
;
;
.
Пример 2. Доказать, что ограничены последовательности:
1)
;
2)
.
Решение. 1) Поскольку
то
,
что и означает ограниченность
.
2) Очевидно, для всех
имеем
.
Так как
,
то, применив неравенство Бернулли,
получим, что для всех
,
откуда
.
Таким образом, для всех
верны неравенства
,
т. е. последовательность ограничена.
Пример 3. Доказать, что не ограничены последовательности:
1)
;
2)
.
Решение. 1) Если
,
то
и
.
Пусть
- произвольное положительное число.
Возьмем четное число
,
большее
(например,
;
тогда
,
т. е. данная последовательность не
ограничена.
2) Из формулы общего члена последовательности имеем:
И, если
то
Но так как
то
.
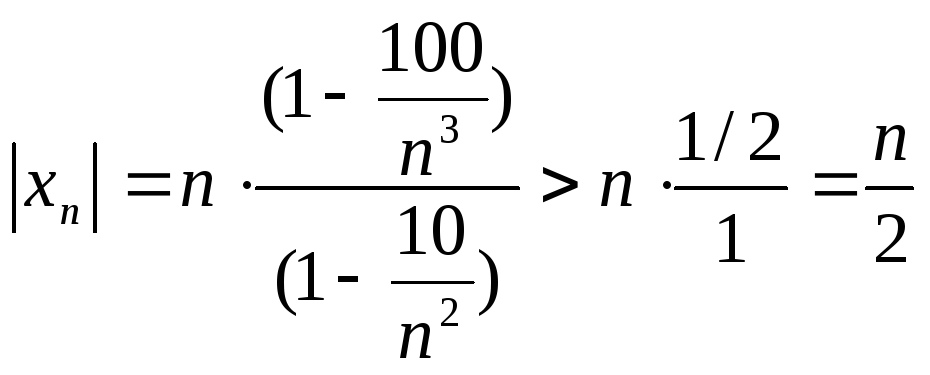Для произвольного положительного числа
возьмем
(например,
);
тогда
,
и, значит, данная последовательность
не ограничена.
Пример 4. Доказать,
что последовательность
,
строго убывает, начиная с некоторого
номера.
Решение. Рассмотрим отношение
.
Видно, что при
,
и, значит,
(так как
).
Итак, данная последовательность строго
убывает, начиная с номера
.
Пример 5. Доказать, что последовательность
строго возрастает.
Решение. Рассмотрим отношение
.
Для любого
из неравенства Бернулли получаем:
.
Откуда следует, что для любого
,
т.е.
,
что и доказывает наше утверждение.
ЗАДАЧИ
Задача 1. Написать пять первых членов каждой из последовательностей:
1)
;
2)
;
3)
;
4)
;
5)
.
Задача 2. Зная несколько первых членов последовательности, написать формулу общего члена последовательностей (выдвинуть какую-либо гипотезу)
1) 1;
;
;
;
2) 1;
;
;
…;
3) 1; 2
;
2
;
3
;
3
;...;
4) 2; 10; 26; 82; 242; 730; ...; 5) -1; 1; -1; 1; -1;....
Задача 3. Написать пять первых членов и формулу общего члена каждой из последовательностей, заданных рекуррентными соотношениями:
1) x1 = 1, xn+1 = xn!; 2) x1 = 1, xn+1 = xn+3; 3) x1 = 1, xn+1 = (n+1) xn;
4) x1 =2, xn+1 =3xn; 5). x1 = 1, xn+1 = x1 + x2 +…+ xn
Задача 4. Выяснить,
какие из чисел
являются членами последовательности
,
если:
1)
;
2)
;
3)
;
4)
.
Задача 5. Является
ли последовательность
подпоследовательностью последовательности
,
если
1)
а)
б)
2)
а)
б)
3)
а)
,
;
б)
.
Задача 6. Какие из последовательностей являются ограниченными:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
.
Задача 7. Доказать ограниченность последовательностей:
1)
;
2)
;
3)
;
4)
;
5)
.
Задача 8. Доказать неограниченность последовательностей:
1)
2)
3)
4)
5)
;
6)
7)
;
8)
.
Задача 9. Доказать, что данные последовательности монотонны, начиная с некоторого номера (своего для каждой последовательности):
1)
2)
3)
4)
;
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
Задача 10. Доказать, что данные последовательности убывают, начиная с некоторого номера (своего для каждой последовательности):
1)
2)
3)
4)
.