Коэффициент концентрации нагрузки kβ

Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор и самих зубчатых колес. Рассмотрим в качестве примера только влияние прогиба валов. Валы прогибаются в противоположные стороны под действием сил в зацеплении.

При симметричном расположении валов их прогиб не вызывает

перекоса зубчатых колес. Это самый благоприятный случай.

При несимметричном и, особенно при консольном расположении, колеса перекошены на угол , что нарушает правильное касание зубьев:

Для абсолютно жестких зубьев 1 и 2 (см. рис) касание происходит только концами. Деформация зубьев сохраняет контакт по всей длине зуба, но нагрузка перераспределяется.

q_cp – средняя интенсивность нагрузки.

При прочих равных условиях влияние перекоса зубьев на коэффициент k_β увеличивается с увеличением ширины колес b_w , поэтому ее ограничивают.

Расчет k_β связан с определением угла перекоса. Это затрудняет точное решение задачи. Поэтому используется приближенная оценка коэффициента по графикам, полученным на основе расчета и практики эксплуатации. Учитывается расположение колес относительно опор и влияние ширины колеса в безразмерном виде коэффициентом .

При проектировании передачи необходимо уменьшать факторы, вызывающие концентрацию нагрузки. Применять жесткие валы, опоры, корпуса. По возможности применять симметричное расположение колес, использовать колеса со срезанными углами.

Диапазон изменения коэффициента концентрации нагрузки различен для контактных и изгибных напряжений, а именно:

k_Нβ = 1,0…1,4. k_Fβ = 1,0….1,9.

Коэффициент динамической нагрузки kν

Этим коэффициентом учитывается только внутренние, т.е. собственные динамические нагрузки, присущие самой зубчатой передаче. Внешние динамические нагрузки, например, от режима работы двигателя, учитывают при выборе допускаемых напряжений. Причиной непостоянства мгновенных значений передаточного отношения является погрешность нарезания зубьев по основному шагу P_b. Это значит, что при ω₁=const_. имеем ω₂const и . В зацеплении появляется дополнительный динамический момент

,

где J – момент инерции ведомых колес.

Отсюда появляется эффект «кромочного удара», который не только увеличивает динамическую нагрузку, но также способствует задиру поверхности зубьев. Для уменьшения вредного влияния этого эффекта применяют фланкирование зубьев, т. е. верхний участок эвольвенты выполняют с отклонением в тело зуба.

В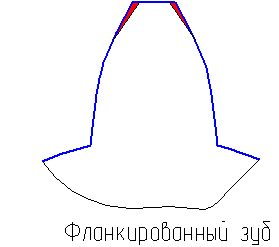еличина дополнительных динамических нагрузок зависит не только от ошибки шага, но и окружной скорости, присоединенных масс, упругости системы и пр. Теоретический расчет k_v сложен, поэтому для приближенной оценки рекомендуются таблицы. Значения коэффициента даются с учетом скорости, степени точности и твердости.

Расчет прямозубых цилиндрических передач на прочность

( по ГОСТ 21354 – 87)

Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом нормальную силу Fn переносят в полюс и раскладывают на окружную (Ft) и радиальную (Fr) составляющие. Такое разложение удобно для расчета валов и опор. Заданы значения моментов Т и диаметры. Отсюда можно определить окружную силу:

,

где d₁ –делительный диаметр. И далее можно записать, что

ЛЕКЦИЯ № 6