4. Устойчивость. Корректность. Сходимость.

1. Устойчивость. Рассмотрим, как влияют погрешности исходных данных на точность окончательных результатов вычислений. Оказывается, что некоторые задачи весьма чувствительны к неточностям в исходных данных. Эта чувствительность характеризуется так называемой устойчивостью.

Пусть в результате решения задачи по исходному значению величины х находится значение искомой величины у. Если исходная величина имеет абсолютную погрешность  х, то решение имеет погрешность  у. Задача называется устойчивой по исходному параметру х, если решение у непрерывно от него зависит, т.е. малое приращение исходной величины  х приводит к малому приращению искомой величины  у. Другими словами, малые погрешности в исходной величине приводят к малым погрешностям в результате расчетов.

Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или вовсе к неверному результату. О подобных неустойчивых задачах также говорят, что они чувствительны к погрешностям исходных данных.

2. Корректность. Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным.

3. Понятие сходимости. Сходимость означает близость получаемого численного решения задачи к истинному решению.

Примеры:

а) Сходимость итерационного процесса.

Для решения задачи (например, нахождение корня нелинейного уравнения) строится метод последовательных приближений. В результате многократного повторения процесса (или итераций) получается последовательность значений х₁, х₂, , х_n. Она сходится к точному решению х = а, если при неограниченном возрастании числа итераций (n  )

.

И в этом случае имеем сходящийся численный метод.

б) Сходимость в методах дискретизации.

Данные методы заключаются в замене задачи с непрерывными параметрами на задачу, в которой значения функций вычисляются в фиксированных точках. Это относится, в частности, к численному интегрированию, решению дифференциальных уравнений и т.д. В данном случае под сходимостью метода понимается стремление значений решения дискретной модели задачи к соответствующим значениям решения исходной задачи при стремлении к нулю параметра дискретизации (например, шага интегрирования).

Итак, для получения решения задачи с необходимой точностью ее постановка должна быть корректной, а используемый численный метод должен обладать устойчивостью и сходимостью.

5. Вычисление значений функций. Вычисление значений многочлена. Схема Горнера.

Пусть необходимо вычислить значение алгебраического многочлена

(5.1)

где (a₀, a₁, , a_n - числовые коэффициенты, n – степень многочлена) при фиксированном x = с.

Поступим следующим образом. Найдем с помощью (п – 1) операций умножения значения степени с, т.е. с², с³, , с^п. Затем в соответствии с (5.1) выполним еще по п операций умножения и сложения. Таким образом, для нахождения Р_п(с) в общем случае потребуется (3п – 1) операций.

Однако более экономным путем вычислений оказывается следующий путь. Многочлен можно представить не в виде (5.1), а в виде

(5.2)

В этом случае вычисление состоит из последовательного нахождения величин:

(5.3)

Нетрудно посчитать, что данная последовательность вычислений состоит из п операций умножения и п операций сложения, т.е. всего из 2п арифметических операций. Нет других способов нахождения значений многочленов при фиксированных х за меньшее число арифметических операций, чем 2п. (При необходимости можно доказать). Описанный способ называется схемой Горнера.

Кроме уменьшения числа операций данная схема хороша еще тем, что благодаря цикличности вычислений при использовании ЭВМ требуется запоминание только одной промежуточной величины b_i или cb_i.

При ручных вычислениях также удобно пользоваться схемой Горнера. При этом обычно пользуются таблицей вида:

Таблица 5.1

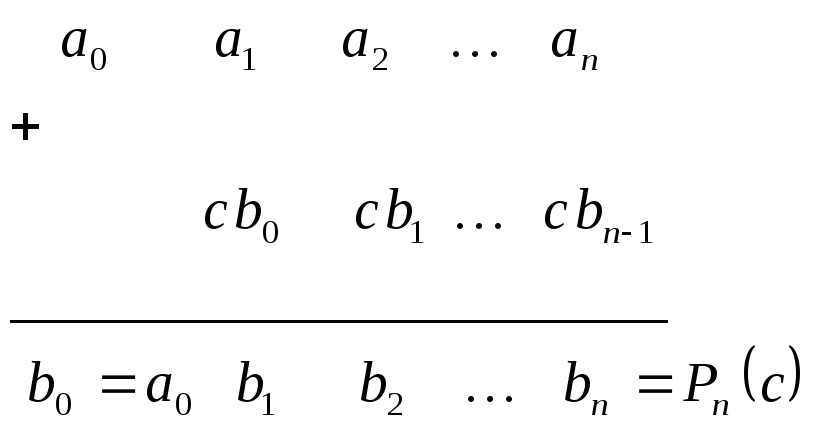
Пример. Вычислить при х = -1,5 значение многочлена.

Таблица 5.2

Решение.

При вычислении многочленов только с четными или только с нечетными показателями степеней х используются методы упрощения. Пусть n = 2k (т.е. P_n (x) - четная функция) и , тогда его можно представить в виде

, (5.4)

Пусть теперь n = 2k + 1, т.е. многочлен является нечетной функцией

Здесь P_n (x) надо представить в виде:

(5.5)

Соответственно, здесь таблица 5.1 будет выглядеть немного по-другому.