
- •2. Елементарні булеві функції та їх властивості.
- •3. Реалізація булевих функцій формулами.
- •4. Рівносильність та тотожність формул. Принцип двоїстості.
- •5. Диз’юнктивна та кон’юнктивна нормальні форми. Розкладання булевої функції за змінними. Досконалі диз’юнктивна та кон’юнктивна нормальні форми.
- •6. Зображення булевих функцій досконалими диз’юнктивними нормальними формами.
- •Для будь-якої формули і для будь-якого числа справедливий розклад:
- •Алгоритм знаходження дкнф для даної функції:
- •Алгоритм знаходження дкнф для даної функції за допомогою рівносильних перетворень:
- •8. Повні системи булевих функцій.
- •Алгоритм побудови скороченої днф
- •2 Етап мінімізації – побудова тупикової днф
- •Алгоритм побудови тупикової днф
- •10. Реалізація булевих функції схемами з функціональних елементів.
- •11. Аналіз і функціонування схеми з функціональних елементів.
- •12. Структурній синтез схем з функціональних елементів.
Для будь-якої формули і для будь-якого числа справедливий розклад:
![]()
![]() (2)
(2)
де
кон’юнкція
береться
за
всіми
![]() можливими наборами
значень
змінних
можливими наборами
значень
змінних
![]() .
.
Рівносильність
(2)
називається розкладом за змінними
![]() .
.
Теорема (про зображення булевих функцій ДКН формами). Будь-яку булеву функцію, відмінну від константи одиниця, можна єдиним чином зобразити ДКН формою:

Алгоритм знаходження дкнф для даної функції:
1) Вибрати всі ті набори значень її змінних, на яких функція набуває значення 0;
2) Для кожного такого набору утворити відповідну повну елементарну диз’юнкцію;
3)
Отримані
повні
елементарні
диз’юнкці
з’єднати
знаками
![]() .
.
Приклад.
Знайти
ДКНФ
для функції
![]() ,
яка реалізується формулою
,
яка реалізується формулою
![]() .
.
Розв’язання: Складемо таблицю істинності:
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
З
таблиці видно, що наборів, на яких функція
набуває
значення
0
два:
![]() і
і
![]() ,
тому
,
тому
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Алгоритм знаходження дкнф для даної функції за допомогою рівносильних перетворень:
1)
Позбавитися у формулі від всіх входжень
знаків
![]() та
та
![]() ;
;
2) Добитися того, щоб знак стояв тільки перд змінними;
3)
поповнити елементарні диз’юнкції до
повних так: якщо змінна
![]() не входить у формулу
не входить у формулу
![]() ,
то оскільки
,
то оскільки
![]() ,
то
,
то
![]() ;
;
4) З однакових членів отриманої кон’юнкції залишаємо тільки один.
Приклад.
Знайти
ДКНФ
для формули
![]() за
допомогою рівносильних перетворень:
за
допомогою рівносильних перетворень:
![]()
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() .
.
8. Повні системи булевих функцій.
Означення.
Система булевых
функцій
![]() називається
повною
(функціонально повною), якщо будь-яка
булева функція
може бути
записана у
вигляді формули
через функції цієї
системи).
називається
повною
(функціонально повною), якщо будь-яка
булева функція
може бути
записана у
вигляді формули
через функції цієї
системи).
Приклад
1 повної системи.
Система
 є
повною.
є
повною.
Приклад
неповної системи.
Система
![]() не
є
повною.
не
є
повною.
Теорема. (про зведення до повної системи). Нехай задані дві системи булевих функцій:
![]() ,
,
![]() ,
,
відносно
яких відомо, що система
![]() повна
і кожна її функція виражається у вигляді
формули через функції системи
повна
і кожна її функція виражається у вигляді
формули через функції системи
![]() .
Тоді система
.
Тоді система
![]() є повною.
є повною.
Теорема (про повноту двоїстої системи функцій). Якщо система булевих функцій є повною, то повною буде і система, яка складається з двоїстих функцій.
Приклади повних систем.
2.
![]() .
.
Дійсно,
візьмемо за систему
![]() систему
систему
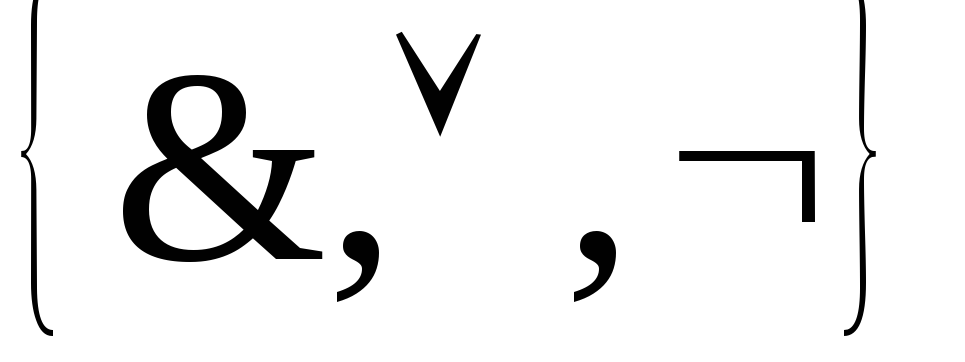 ,
а за систему
,
а за систему
![]() – дану систему
– дану систему
![]() .
Скористаємося рівносильністю
.
Скористаємося рівносильністю
![]() .
В результаті будь-яка булева функція,
зображена формулою через функції системи
.
В результаті будь-яка булева функція,
зображена формулою через функції системи
![]() виявиться зображеною формулою через
функції системи
виявиться зображеною формулою через
функції системи
![]() ,
тобто система
,
тобто система
![]() є повною.
є повною.
3.
![]() .
.
4.
![]() .
.
5. {|}.
6.
![]() .
.
7.
Система
![]() ,
де
,
де
![]() – додавання за модулем 2, є
повною.
– додавання за модулем 2, є
повною.
З наведених прикладів видно, що існує ціла низка повних систем функцій. Кожна з цих систем може бути прийнята за множину елементарних функцій. Таким чином, для зображення булевої функції можна використовувати різні повні системи.
Означення.
Система функций
![]() називається
базисом, якщо
вона є
повною,
але будь-яка її
підсистема не
буде повною.
називається
базисом, якщо
вона є
повною,
але будь-яка її
підсистема не
буде повною.
9. Мінімізація булевих функції в класі
досконалих диз’юнктивних нормальних форм.
Означення.
Мінімальною ДНФ
(МДНФ) функції
![]() називається ДНФ, що реалізує функцію
називається ДНФ, що реалізує функцію
![]() і містить мінімальне число символів
змінних у порівнянні з усіми іншими
видами ДНФ, що реалізують функцію
і містить мінімальне число символів
змінних у порівнянні з усіми іншими
видами ДНФ, що реалізують функцію
![]() .
.
Метод Квайна-МакКласкі мінімізації булевих функцій в класі ДНФ
1 етап мінімізації – побудова скороченої ДНФ
Позначимо
через
![]() одиничну множину функції
одиничну множину функції
![]() ,
тобто множину наборів значень аргументів
функції
,
тобто множину наборів значень аргументів
функції
![]() ,
на яких вона набуває значення 1.
,
на яких вона набуває значення 1.
Означення.
Імплікантом
функції
![]() називається елементарна кон’юнкція
називається елементарна кон’юнкція
![]() така, що
така, що
![]() .
.
Означення.
Імплікант
![]() функції
функції
![]() називається простим
імплікантом (ПІ),
якщо після виключення будь-якої змінної
з
називається простим
імплікантом (ПІ),
якщо після виключення будь-якої змінної
з
![]() утворюється елементарна кон’юнкція,
яка вже не є імплікантом функції
утворюється елементарна кон’юнкція,
яка вже не є імплікантом функції
![]() .
.
Прості
імпліканти – це найкоротші з імплікантів,
які складаються з одних й тих самих
змінних. Наприклад, для функції
![]() кон’юнкції
кон’юнкції
![]() ,
,
![]() - прості імпліканти, а
- прості імпліканти, а
![]() - імплікант, але не простий. Відзначимо,
що будь-яка кон’юнкція будь-якої ДНФ
даної функції є імплікантом цієї функції.
- імплікант, але не простий. Відзначимо,
що будь-яка кон’юнкція будь-якої ДНФ
даної функції є імплікантом цієї функції.
Теорема. Будь-яка булева функція реализується диз’юнкцією всіх своїх простих імликантів ).
Означення.
Скороченою
ДНФ
(СДНФ) функції
![]() називається диз’юнкція всіх простих
імплікантів функції
називається диз’юнкція всіх простих
імплікантів функції
![]() .
.
