21

Розділ 2

Елементи теорії булевих функцій

1. Поняття булевої функції. Способи завдання булевих функцій.

Число булевих функцій аргументів.

Булеві функції застосовуються в обчислювальній техніці для опису пристроїв переробки дискретної інформації, яка розкладається на елементарні одиниці – біти, які в цих пристроях реалізуються сигналами, що описуються двійковими змінними – булевими змінними.

Нехай задана множина змінних і множина .

Означення. Булевою функцією називається функція , яка визначена і набуває своїх значень на множині . Отже, .

Оскільки множина скінченна, то задати відображення означає задати множину наборів з і для кожного набора вказати його образ в .

Позначимо набір значень змінних через . Таким чином, булева функція ставить у відповідність кожному упорядкованому набору , якій складається з 0 і 1, або 0, або 1. Набір називають ще двійковим.

Лема. Число різних наборів , , значень для аргументів булевої функції дорівнює .

Приклад. Для функції можна задати різних двійкових

наборів значень аргументів :

0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Означення. Булева функція називається цілком визначеною, якщо її значення визначено для всіх двійкових наборів, інакше булева функція називається не цілком визначеною або частковою.

Означення. Двійковий набір, на якому булева функція обертається в 0, називається нульовим. Двійковий набір, на якому булева функція обертається в 1, називається одиничним. Набір, на якому функція не визначена, називається байдужим.

Якщо k двійкових наборів функції є байдужими, то часткову функцію можна довизначити способами. Інакше кажучи, кожній такій частковій функції відповідає множина з цілком визначених булевих функцій, отриманих шляхом різних довизначень.

Означення. Змінна , яка є аргументом булевої функції , називається неістотною (фіктивною), якщо = при будь-яких значеннях інших змінних, тобто якщо зміна значення в будь-якому наборі значень змінних не змінює значення функції. В цьому випадку функція істотно залежить від -1 змінної.

Означення. Константою 0 (константою 1) називається цілком визначена булева функція, яка на всіх наборах дорівнює 0 (1), тобто функція з неістотними змінними.

Означення. Констітуентою 0 (констітуентою 1) називається цілком визначена булева функція, яка тільки на одному наборі дорівнює 0 (1).

З означення випливає, що для задання булевої функції достатньо вказати, які значення функції відповідають кожному з наборів значень аргументів, тобто скласти таблицю, яка називається таблицею істинності булевої функції:

Таблиця істинності – таблиця, в якій кожному двійковому набору значен змінних ставиться у відповідність значення функції на даному наборі або прочерк, якщо значення функції на даному наборі не визначено. В останньому випадку байдужий набір в таблицю можна не включати.

			…
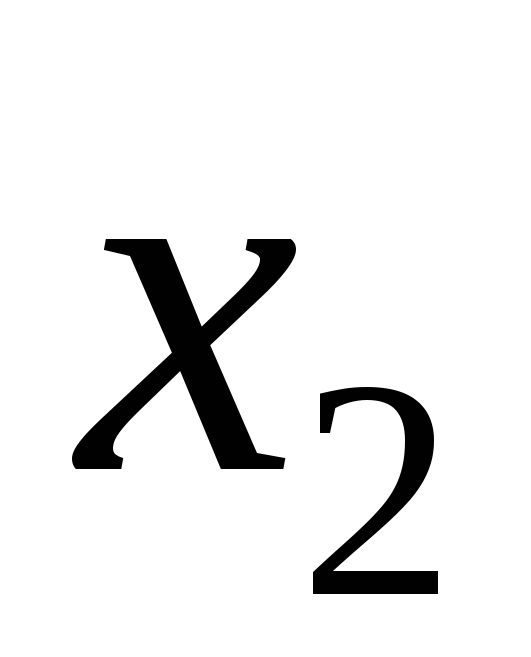
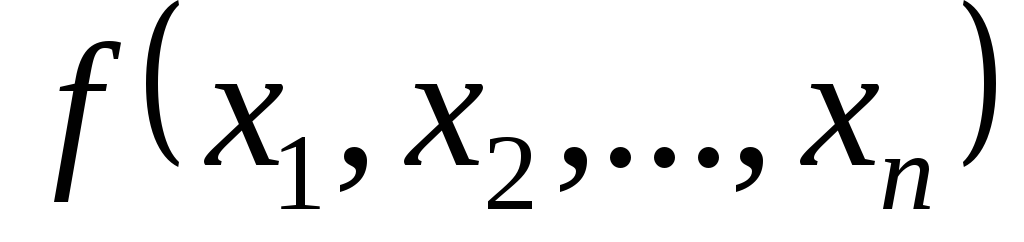
0	0		…		0
0	0		…		1
…	….		…		…			…
1		2		…	n				,
…		…		…	…			…
1		1		…		1

Двійковий набір можна прочитати як -розрядне ціле двійкове число. В силу цього рядки в таблиці істинності зручно розташовувати в природному порядку зростання двійкових чисел , а десятковий еквівалент даного числа вважати номером відповідного двійкового набору.

Приклад. Нехай =3. Розглянемо довільну функцію трьох змінних

номер набору
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	0
4	1	0	0	1
5	1	0	1	1
6	1	1	0	0
7	1	1	1	0

Як видно з таблиці, число різних наборів аргументів дорівнює , функції відповідає двійковий вектор довжини . Звідки випливає ще один спосіб задання булевої функції – векторний, коли булева функція подається у вигляді , .

Розглядаючи двійковий вектор як двійкове ціле число з розрядами, будемо вважати десятковий еквівалент цього двійкового числа номером (індексом) функції, яка задана даною таблицею. В нашому випадку задана функція .

Ще один спосіб задання булевої функції – геометричний, коли булева функція задається сукупністю всіх векторів, значення функції на яких дорівнює 1. (сукупністю одиничних векторів).

Приклад. Розглянемо геометричну інтерпретацію області визначення булевої функції 3-х хмінних – множину вершин одиничного куба.

При на векторах, позначених зірочкою, функція обертається в 1.

– вказані номери векторів.

Теорема (про число булевих функцій від аргументів). Кількість різних булевих функцій від аргументів дорівнює .

Доведення. Для задання булевої функції від аргументів треба вказати її значення для кожного з різних наборів значень її аргументів, тобто заповнити правий стовпець таблиці істинності функції. Оскільки порядок рядків в таблиці однаковий, то різних булевих функцій від аргументів існує стільки, скільки можна скласти різних правих стовпців. А оскільки кожний стовпець являє собою двійковий набір довжини , то кількість таких наборів за лемою дорівнює .■

Відзначимо, що із зростанням кількість різних булевих функцій від аргументів швидко зростає: при =1 їх 4, при =2 їх 16, при =3 – 256, при =4 – 655536 і т.д. Із зростанням кількості аргументів, таблиця, що задає булеву функцію, дуже ускладнюється; вже при =10 таблиця стає величезною (1024 рядки), а при =20 – практично неосяжною. Тому при великих табличний спосіб завдання булевих функцій незастовоний.

2. Елементарні булеві функції та їх властивості.

Розглянемо булеві функції, які часто застосовуються в логіці і кібернетиці і відіграють таку ж само важливу роль як, наприклад, степенева функція або функція в аналізі, тому їх також називаєть елементарними.

Нехай n=1. Число різних наборів дорівнює , число різних функцій від однієї змінної дорівнює . Побудуємо таблицю функцій при n = 1.

	Позначення
	0			1
0 1	0 0	0 1	1 0	1 1

Ці функції однієї змінної вважаються елементарними.

Назви: =0 – константа 0;

= – тотожня функція;

= – заперечення;

=1 – константа 1.

Нехай n=2. Число різних наборів дорівнює , число різних функцій від однієї змінної дорівнює . Побудуємо таблицю функцій при n = 2.

		Позначення
		0														|	1
0 0 1 1	0 1 0 1	0 0 0 0	0 0 0 1	0 0 1 0	0 0 1 1	0 1 0 0	0 1 0 1	0 1 1 0	0 1 1 1	1 0 0 0	1 0 0 1	1 0 1 0	1 0 1 1	1 1 0 0	1 1 0 1	1 1 1 0	1 1 1 1

Функції в таблиці перенумеровані так, що номер функції, записаний в двійковій системі числення, дає послідовність значень відповідної функції.

Деякі з цих функцій мають спеціальні назви і позначення. Всі функції можна розбити на пари, в яких кожна функція є запереченням іншої. Розглянемо ці пари:

0) – константа 0; – константа 1;

1) – кон’юнкція; | – штрих Шеффера;

2) – імплікація; ;

3) ; ;

4) ; ;

5) ; ;

6) – еквіваленція; – додавання за модулем 2 (сума Жегалкіна);

7) – диз’юнкція; – стрілка Пірса.

Всі ці функції від двох аргументів ми будемо називати елементарними булевими функціями. При цьому основними елементарними функціями є кон’юнкція, диз’юнкція і заперечення.

Символи і т.д., які беруть участь в позначеннях елементарних функцій, називаються логічними зв’язками.

За допомогою таблиць, які визначають основні елементарні булеві функції, можна встановити їх властивості: комутативність, асоціативність та ідемпотентність і , дистрибутивність відносно і відносно , закони де Морагана, дії з 0 і 1 та інші.

Крім того, справедливі рівності, які виражають одні елементарні булеві функції через інші, наприклад:

1) ;

2) ;

3) |;

4) =;

5) |=(|)|(|);

6) =()();

7) =|;

8) =.