
- •1. Дійсні Числа
- •2. Комплексні числа та дії над ними
- •3. Поняття функції. Область визначення.
- •8.Означення похідної
- •9. Похідна суми, добутку, частки функції.
- •10. Диференціал.
- •12. Правило Лопіталя
- •14. Формула Тейлора
- •15. Опуклість кривої, точки перегину, асимптоти кривої.
- •22. Невизначений інтеграл. Означення та властивості.
- •24. Формула інтегрування по частинам у невизначеному інтегралі.
- •25. Інтегрування раціональних дробів.
- •27. Визначений інтеграл. Означення та властивості.
- •28.Формула Ньютона – Лейбніца:
- •37. Ряди: означенняб необхідна умова збіжності
- •38.Ряди: ознаки збіжності Даламбера, Коші, інтегральна ознака, ознака порівняння.
- •40. Степеневі ряди, радіус та область збіжності.
1. Дійсні Числа
Множина сукупність деяких об’єктів об’єднаних за певною ознакою або властивістю.
Натуральні числа – використовуються при лічбі предметів.
Ірраціональні числа – представляються у вигляді не скінченних, не періодичних дробів.
Раціональні й Ірраціональні утворюють множину дійсних чисел.
Дійсні числа поділяються на 2-ві групи:
-
Трансциндентні
-
Алгебраічні
2. Комплексні числа та дії над ними
Комплексными числами називають вирази виду а + bi (a i b — дійсні числа, i — деякий символ), для яких поняття piвностi та операції додавання i множення вводяться так:
а) два
комплексш числа
![]() і
і
![]() piвнi
тoдi
i
тiльки
товi,
коли
piвнi
тoдi
i
тiльки
товi,
коли
![]() і
і
![]()
б) сумою
чисел
![]() і
і
![]() називають
число
називають
число
![]()
в) добутком
чисел
![]() і
і
![]() називають
число
називають
число
![]()
Отже, додавання i множення комплексних чисел виконують за формулами:
![]() (1)
(1)
![]() (2)
(2)
Операції додавання (1) i множення (2) мають такі властивості
-
Комутатившсть додавання:

-
AcouiaTHBHicTb додавання:

-
Для будь-яких комплексних чисел z1 i z2 icнye таке комплексне число z, що z1 + z = z2. Це число називаеться різницею чисел z2 i z1, його позначають z2 — z1.
-
Комутативн1сть множення:

-
AcouiaTHBHicTb множення:

-
Для будь-яких комплексних
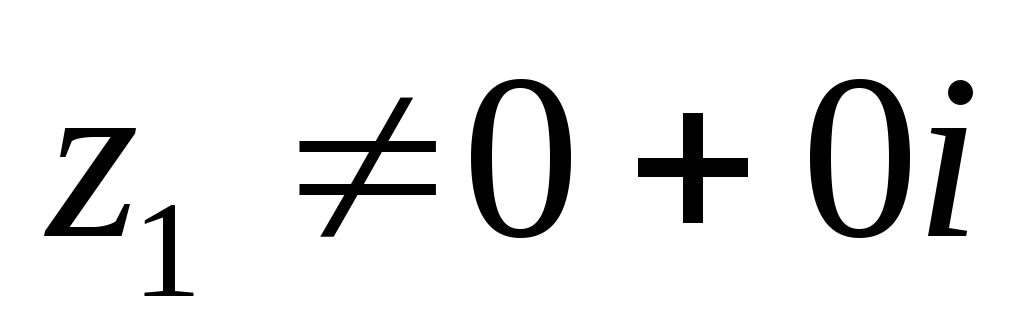 i
z2
icнye
таке число z,
що
z1z
=z2.
Це число називаеться
часткою
комплексних чисел z2
i
zx;
його позначають
i
z2
icнye
таке число z,
що
z1z
=z2.
Це число називаеться
часткою
комплексних чисел z2
i
zx;
його позначають
 .
Ділення
на
комплексне
число 0+0і,
яке називаеться
нулем,
неможливе.
.
Ділення
на
комплексне
число 0+0і,
яке називаеться
нулем,
неможливе. -
Дистрибутившсть:

3. Поняття функції. Область визначення.
Фу́нкція — це правило, яке кожному елементу з першої множини (області визначення) ставить у відповідність один і тільки один елемент з другої множини. Часто цю другу множину називають цільовою множиною чи образом функції чи відображення.
Область визначення — множина допустимих значень аргументу функції. Позначається як D(y), якщо вказується область визначення функції y=f(x).
Якщо задані: числова
множина
![]() та
правило
та
правило
![]() ,
що дозволяє поставити у відповідність
кожному елементу
,
що дозволяє поставити у відповідність
кожному елементу
![]() з
множини
з
множини
![]() певне
число, то говорять, що задана функція
певне
число, то говорять, що задана функція
![]() з
областю
визначення
з
областю
визначення
![]() .
.
Тобто, визначення області значень є необхідною умовою визначення функції.
Значення змінних,
на яких задається функція
![]() ,
називають допустимими
значеннями змінних.
,
називають допустимими
значеннями змінних.
Значення змінних,
при яких алгебраїчний вираз
![]() має
зміст, називають допустимими
значеннями змінних.
Множину всіх
допустимих значень змінних
називають областю
допустимих значень змінних
має
зміст, називають допустимими
значеннями змінних.
Множину всіх
допустимих значень змінних
називають областю
допустимих значень змінних
![]() .
.
Областю
визначення рівняння
![]() називають
множину всіх тих значень зміної x,
при яких алгебраїчні вирази
називають
множину всіх тих значень зміної x,
при яких алгебраїчні вирази
![]() і
і
![]() одночасно
мають зміст.
одночасно
мають зміст.
Якщо функція задана формулою, то область визначення складається зі всіх значень незалежної змінної, при яких формула має зміст.
4. Обернені функції
Функція, яка приймає кожне своє значення в єдиній точці області визначення, є оберненою.
у такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає.
5. Побудова графіків функцій та елементарні перетворення (стиск, розтяг та паралельне перенесення).
Стискування: Графік функції y = f(ах) (а > 1) виходить за допомогою стискування графіка функції y = f(x) уздовж осі х в а разів.
Розтягування: Графік функції y=f(ах) (1 > а > 0) виходить за допомогою розтягування графіка функції у = f(x) уздовж осі х в 1/а разів. При цьому в обох випадках точки пересічення графіка з віссю в остаються незмінними
6. Числові послідовності. Грнаниця послідовності
Число а- назив
границею
послідов
![]() де
n
прямує до 0якщо у будь-якому
епселент числа a
знаходиться
усі члени цієї послідовності.
де
n
прямує до 0якщо у будь-якому
епселент числа a
знаходиться
усі члени цієї послідовності.
7. Неперервність ф-ції. Точки розриву та їх класифікація.
Функція
f(х),
визначена в деякому околі точки х0
називається неперервною
в точці х0,
якщо виконується умова:

Функція f(х)
називається неперервною
в області свого визначення,
якщо приріст функції
![]() дорівнює нулю, коли приріст аргументу
дорівнює нулю, коли приріст аргументу
![]() прямує до нуля:
прямує до нуля:![]()
Якщо функція неперервна в кожній точці деякої області (відрізка, числової вісі тощо), то вона називається неперервною в цій області.
Якщо функція f(х), неперервна в околі точки х0, не є неперервною в ній, то х0 - точка розриву заданої функції.
Класифікація точок розриву функції:
якщо односторонні
границі функції f(х)
існують, але
 ,
то
х0
,
то
х0
-усувний розрив 1-го роду;
якщо існують
односторонні границі функції f(х)
і
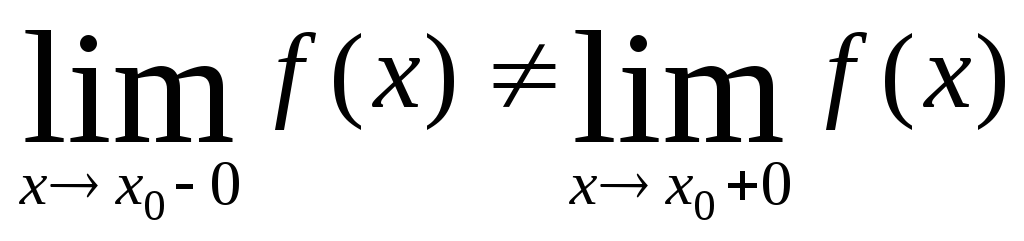 ,
то
х0
– розрив
1-го роду і в
точці х0
має стрибок
,
то
х0
– розрив
1-го роду і в
точці х0
має стрибок
 ;
;
якщо хоча б одна з односторонніх границь функції f(х) в точки х0 не існує, то х0
-точка розриву ІІ-го роду.
