10. Доказательство достаточности принципа виртуальных напряжений

Докажем достаточность принципа, то есть, покажем, что выполнение вариационного уравнения Кастильяно имеет следствием удовлетворение уравнений совместности и кинематических краевых условий.

Рассматриваемые вариации поля напряжений статически допустимы:

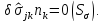
Введем в области 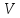некоторое произвольное векторное поле , обладающее свойствами непрерывности и дифференцируемости. К первому из соотношений, определяющих статически допустимые вариации, применим оператор 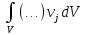. Полученное выражение

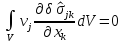
преобразуем с использованием интегральной формулы Гаусса-Остроградского

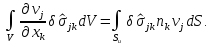
Вследствие симметрии тензора напряжений антисимметричная часть тензора 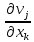несущественна, и выражение может быть представлено в виде

В последних выражениях при интегрировании по поверхности 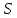использовано второе соотношение, определяющее статически допустимые вариации. Произведем почленное вычитание из вариационного уравнения Кастильяно:

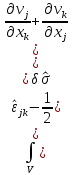
Вследствие произвольности вариаций 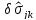в объеме тела и на части поверхности 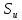из полученного соотношения следует

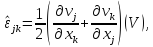
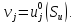
Таким образом, из предположения о статической допустимости деформаций при удовлетворении вариационного уравнения Кастильяно следует:

- существование непрерывного векторного поля 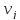, связанного с распределением деформаций соотношениями Коши (распределение деформаций геометрически допустимо в смысле удовлетворения условиям совместности);

- удовлетворение векторным полем 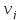кинематических условий краевой задачи.

Остальные уравнения (уравнения равновесия и закон упругости) и статические краевые условия удовлетворены по определению статической допустимости. Вследствие единственности решения основной краевой задачи теории упругости векторное поле 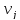тождественно распределению перемещений в состоянии равновесия. Достаточность принципа виртуальных напряжений доказана.

11. Вариационный принцип Кастильяно

Введем на множестве статически допустимых распределений напряжений 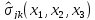в объеме тела 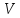функционал дополнительной потенциальной энергии системы 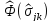согласно соотношению

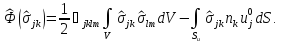
Первый член представляет потенциальную энергию упругой деформации 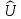как квадратичную форму напряжений, второй – работу статически возможных напряжений на заданных перемещениях

Вариация функционала 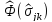может быть представлена в виде

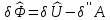
и согласно принципу виртуальных напряжений обращается в нуль в истинном состоянии равновесия:

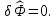
Полученное вариационное уравнение называется вариационным принципом Кастильяно.

Формулировка. В истинном состоянии равновесия функционал дополнительной потенциальной энергии системы принимает стационарное значение на множестве смежных статически допустимых состояний.

12. Характер стационарной точки функционала дополнительной потенциальной энергии. Теорема Кастильяно

Для установления характера стационарной точки исследуем знак второй вариации функционала дополнительной энергии. Работа внутренних сил на заданных перемещениях является линейной формой напряжений, следовательно, соответствующая вторая вариация обращается в нуль, и имеет место соотношение

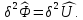
Исследуем знак второй вариации плотности потенциальной энергии упругой деформации

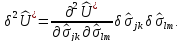
Применяя формулу Кастильяно и закон линейной упругости, получим

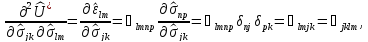
где 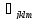- тензор упругих податливостей, 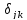- символ Кронекера.

Компоненты тензора являются коэффициентами положительно определенной квадратичной формы, следовательно,

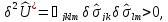
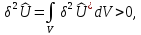
то есть, стационарная точка функционала дополнительной потенциальной энергии является точкой минимума.

На этой основе формулируется теорема о минимуме дополнительной потенциальной энергии системы (теорема Кастильяно).

Формулировка. В истинном состоянии равновесия дополнительная потенциальная энергия системы принимает минимальное значение на множестве смежных статически допустимых состояний.