7. Вариационный принцип Лагранжа

Предположим внешние воздействия потенциальными. Рассмотрим полную потенциальную энергию системы как функционал, определенный на множестве кинематически допустимых состояний

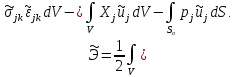
Из формулировки принципа виртуальных перемещений непосредственно следует, что истинное состояние равновесия определяется условием

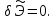
Полученное вариационное уравнение называется вариационным принципом Лагранжа.

Формулировка. В истинном состоянии равновесия функционал полной потенциальной энергии принимает стационарное значение на множестве смежных кинематически допустимых состояний.

Рассмотрим простейший иллюстрирующий пример. Пусть на линейно упругий элемент с коэффициентом жесткости 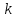действует внешняя сила 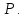Равновесие этой системы характеризуется условием 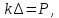где - абсолютное удлинение упругого элемента.

Определим потенциальную энергию деформации и работу внешней нагрузки (в данном случае кинематически возможным является произвольное значение удлинения ):

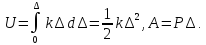
Полная потенциальная энергия системы 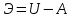представляется функцией переменной Из условия экстремума функции

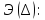
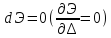
очевидным образом следует уравнение равновесия

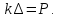
8. Характер стационарной точки функционала полной потенциальной энергии. Теорема Лагранжа

Характер стационарной точки функционала определяется знаком второй вариации. Рассмотрим вторую вариацию функционала полной потенциальной энергии на множестве смежных кинематически допустимых состояний

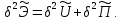
Как было показано выше, потенциальная энергия внешних сил является линейной формой перемещений. Вариация на кинематически допустимых распределениях перемещений выражается соотношением

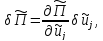
при этом, коэффициенты вариации 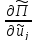не зависят от перемещений 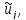следовательно, 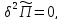и знак второй вариации полной потенциальной энергии 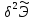определяется знаком второй вариации потенциальной энергии упругой деформации .

Плотность потенциальной энергии упругой деформации является квадратичной формой деформаций. В смежном кинематически допустимом состоянии эта величина может быть представлена в виде

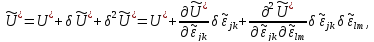
где 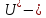плотность энергии деформации в состоянии равновесия.

Исследуем знак второй вариации 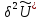в окрестности состояния равновесия. Применяя формулу Грина и закон линейной упругости, получим

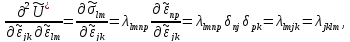
где 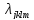- тензор коэффициентов упругости, 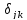- символ Кронекера.

Компоненты тензора 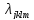являются коэффициентами положительно определенной квадратичной формы, следовательно,

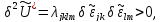
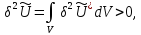
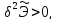
то есть, стационарная точка функционала полной потенциальной энергии является точкой минимума.

На этой основе формулируется теорема о минимуме полной потенциальной энергии системы (теорема Лагранжа).

Формулировка. В истинном состоянии равновесия полная потенциальная энергия системы принимает минимальное значение на множестве смежных кинематически допустимых состояний.

9. Принцип виртуальных напряжений (вариационное уравнение Кастильяно)

Рассмотрим совокупность смежных статически допустимых состояний

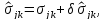
где 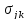- распределение напряжений в состоянии равновесия, 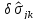- статически допустимая вариация, удовлетворяющая соотношениям

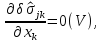
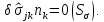
Составим интегральные уравнения равновесия для смежного статически возможного состояния:

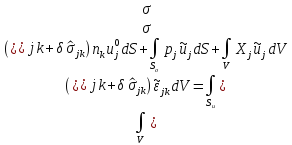
и для состояния равновесия:

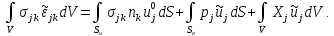
Почленно вычитая, получим тождество

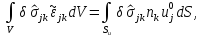
которому удовлетворяет любое кинематически возможное распределение деформаций

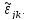
Если рассматривать множество статически допустимых деформаций

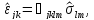
то единственным элементом, удовлетворяющим полученному соотношению, будет распределение, которое является одновременно статически и кинематически возможным, то есть распределение деформаций в истинном состоянии равновесия. Получаем вариационное уравнение Кастильяно

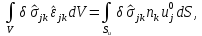
позволяющее выделить из множества статически возможных состояний истинное состояние равновесия.

В соответствии с формулами Коши

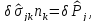
где 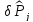- статически возможная вариация вектора напряжений на части ограничивающей поверхности 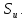Тогда выражение в правой части уравнения Кастильяно приобретает смысл виртуальной работы внутренних сил на заданных перемещениях

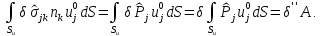
Левая часть уравнения представляет собой, в соответствии с формулой Кастильяно, статически допустимую вариацию потенциальной энергии упругой деформации:

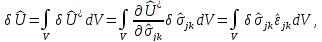
где 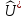- плотность потенциальной энергии упругой деформации.

Полученный результат можно представить в форме принципа виртуальных напряжений.

Формулировка. Для того, чтобы данное статически возможное состояние являлось состоянием равновесия, необходимо и достаточно, чтобы статически возможная вариация потенциальной энергии упругой деформации была равна виртуальной работе внутренних сил на заданных перемещениях:

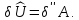
Приведенное выше доказательство показывает необходимость выполнения принципа виртуальных напряжений для состояния равновесия.