Физика 3 семестр / новая папка / Помощь к экзамену / Темы / 02.Электрическое поле

Электрическое поле, создаваемое заряженными телами, неподвижными относительно инерциальных систем отсчета, называется электростатическим полем.

1.2. Напряженность электрического поля. Силовые линии

Наличие электрического поля в какой-либо точке пространства можно зарегистрировать по силовому действию поля на помещенный в эту точку заряд. Назовем пробным электрическим зарядом положи-тельный точечный заряд настолько малой величины, что его внесение в поле не вызывает изменения значений и перераспределения в пространстве зарядов, создающих исследуемое поле.

Количественной характеристикой силового действия электрическо-го поля на заряженные частицы и тела служит векторная величина – напряженность электрического поля. Напряженность электричес-кого поля равна отношению силы, действующей со стороны поля на неподвижный пробный электрический заряд, помещенный в рассматриваемую точку поля, к этому заряду:

. (1.4)

Будем называть электрическое поле однородным, если во всех его точках векторы напряженности одинаковы, т.е. совпадают по модулю и направлению.

Сила, действующая со стороны электрического поля на помещенный в него произвольный точечный заряд, равна

, (1.5)

однако в отличие от выражения (1.4) здесь – напряженность в точке расположения заряда q для поля, в общем случае отличном от того, которое было до внесения в него заряда q.

В случае нахождения силы, действующей на неточечный заряд Q, помещенный в электрическое поле, необходимо поступать следующим образом. Разобьем исследуемое заряженное тело на совокупность материальных точек, т.е. на точечные заряды (рис.1.2). Элементарная сила со стороны поля, действующая на каждый точечный заряд – элемент заряда Q – определится как , где – напряженность поля в точке расположения заряда . Тогда общая сила, действующая на весь заряд Q, будет найдена путем суммирования элементарных сил:

, (1.6)

где интегрирование проводится по всему объему тела.

Практическое вычисление интеграла (1.6) оказывается удобным, если электрический заряд распределен по всему заряженному телу непрерывно – вдоль некоторой линии, по поверхности или по объему. В этих случаях можно использовать понятия линейной, поверхностной и объемной плотностей зарядов (рис.1.3). Линейная плотность электрических зарядов

,

где – заряд малого участка заряженной линии (пример: стержень, нить) длиной (рис.1.3, а). Поэтому полный заряд тела можно найти как . Если заряд распределен по линии равномерно, то полный заряд тела будет равен . Размерность линейной плотности зарядов в СИ: .

Поверхностная плотность электрических зарядов

,

где – заряд малого участка заряженной поверхности (пример: заряженная плоскость) площадью (рис.1.3, б). Полный заряд тела можно рассчитать как . При равномерно распределенном по поверхности заряде полный заряд тела будет равен . Размерность поверхностной плотности зарядов в СИ: .

Объемная плотность электрических зарядов

,

где – заряд малого элемента заряженного тела объемом (рис.1.3, в). Полный заряд тела можно рассчитать как . При равномерно распределенном по объему заряде полный заряд тела будет равен . Размерность объемной плотности зарядов в СИ: .

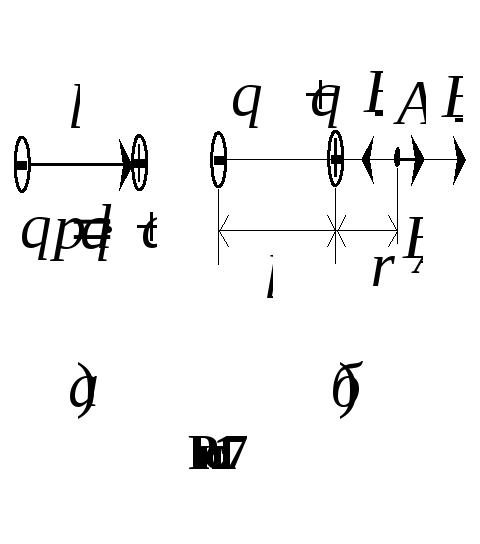
В качестве примера определения напряженности электростатического поля заряженного тела по заданному распределению зарядов рассмотрим нахождение напряженности поля точечного заряда Q (рис.1.4). Модуль силы, действующей со стороны такого поля на помещенный в него пробный заряд , определится, согласно (1.1), как , где r – расстояние от источника поля (заряда Q) до исследуемой точки поля (заряда ), отсчитываемое вдоль некоторой оси Or. Тогда

. (1.7)

Напряженность поля в точках пространства, в которых расположены точечные заряды, неопределена.

1.3. Суперпозиция электростатических полей

При рассмотрении электростатического поля произвольной системы неподвижных точечных зарядов было экспериментально показано, что результирующая сила , действующая на пробный заряд q в любой точке поля, равна геометрической сумме сил, действующих на заряд q со стороны каждого из зарядов :

. (1.8)

Из (1.8) легко получить, что

. (1.9)

Последнее соотношение выражает принцип суперпозиции электрических полей (принцип независимости действия электрических полей): напряженность электрического поля, созданного системой зарядов в любой точке пространства, равна векторной сумме напряженности полей, созданных каждым зарядом в отдельности в этой точке.

Рассмотрим применение этого принципа для расчета напряженности поля системы дискретно и непрерывно распределенных зарядов.