Физика 3 семестр / новая папка / Помощь к экзамену / Темы / 36.Электромагнитная волна

9.6. Уравнение электромагнитной волны

Рассмотрим систему дифференциальных уравнений Максвелла (8.15) и решим ее, получив законы изменения напряженностей магнитного и электрического полей. С этой целью воспользуемся первым и вторым уравнениями системы (8.17) и преобразуем (8.15), рассмотрев существование электрического и магнитного полей в отсутствии свободных зарядов и токов проводимости. В таком случае и :

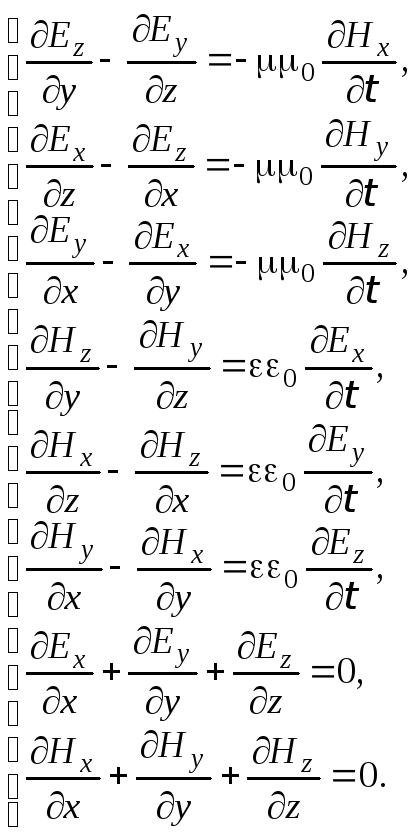(9.30)

Метод решения данной системы уравнений заключается в их объединении. Выберем четвертое уравнение системы и продифференцируем его по времени:

; .

Поскольку смешанная производная не зависит от порядка переменных, по которым берутся производные, то

.

Теперь в правую часть уравнения подставим и , взяв их из третьего и второго уравнений системы (9.30):

.

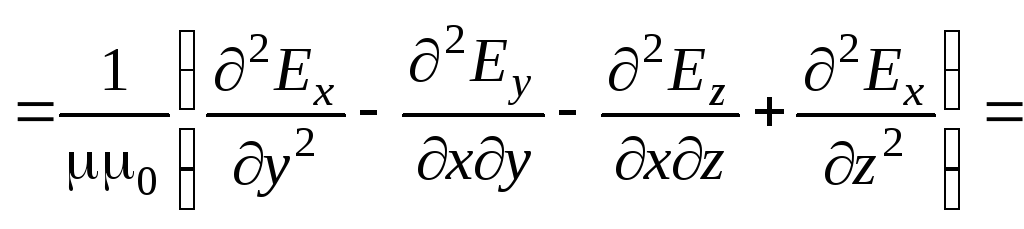
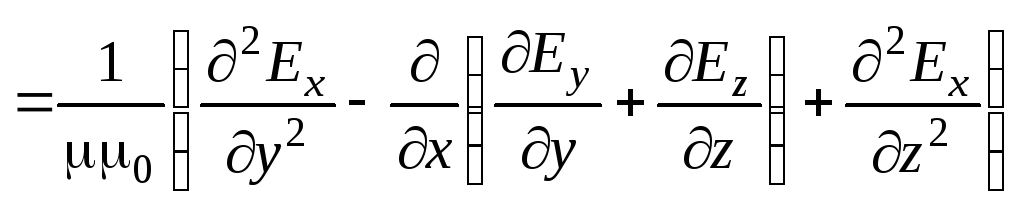Теперь воспользуемся седьмым уравнением системы (9.30) и получим

.

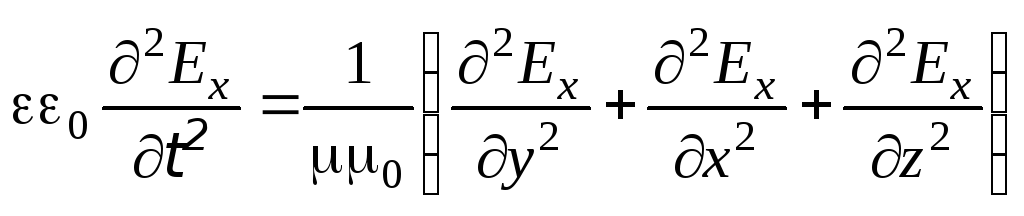Это уравнение можно записать таким образом:

.

Аналогичные уравнения можно получить и для других проекций напряженности электрического поля:

; .

Обобщая три последних соотношения, запишем

. (9.31)

Аналогично можно получить

. (9.32)

Полученные уравнения (9.31) и (9.32) по своему виду соответствуют волновому уравнению (9.29). А поэтому из уравнений Максвелла следует, что электромагнитное поле, т.е. совокупность переменных электрического и магнитного полей, распространяется в пространстве в виде волны со скоростью

. (9.33)

Распространяющееся в пространстве электромагнитное поле называется электромагнитной волной. Такая волна переносит из одной точки пространства в другие колебания напряженностей электрического и магнитного полей.