Основные свойства двойного интеграла

1. .

2. .

3. , где – площадь области интегрирования .

4. Если область интегрирования разбита на две области и , то

=+.

5. Оценка двойного интеграла. Если , то

.

Правила вычисления двойных интегралов

Различают два основных вида области интегрирования.

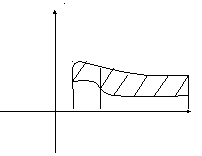
1. Область интегрирования ограничена слева и справа прямыми , , а снизу и сверху – непрерывными кривыми , , каждая из которых пересекается вертикальной прямой только в одной точке (рис. 5).

Y

D

c X

Рис. 5.

Для такой области двойной интеграл вычисляется по формуле

,

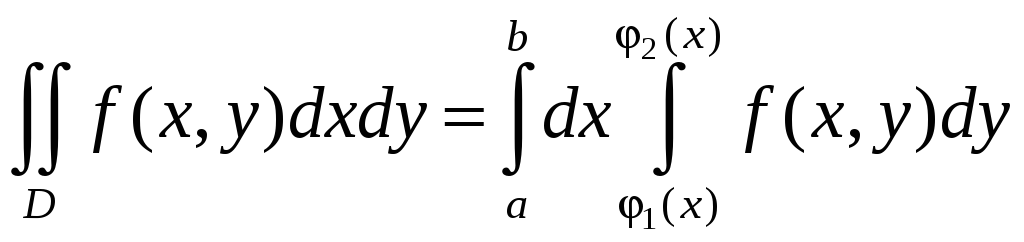причем сначала вычисляется внутренний интеграл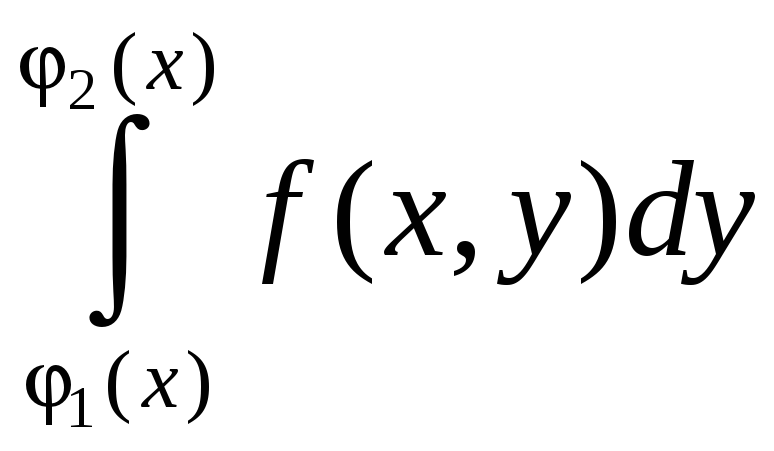, в котором х считается постоянным.

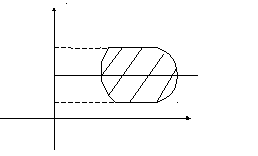
2. Область интегрирования ограничена снизу и сверху прямыми , , а слева и справа – непрерывными кривыми , , каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 6).

Для такой области двойной интеграл вычисляется по формуле

,

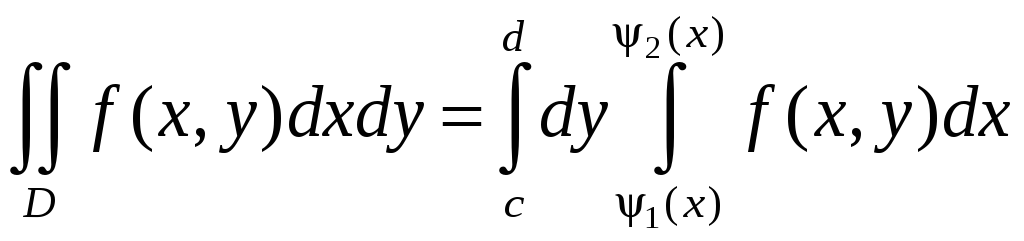причем сначала вычисляется внутренний интеграл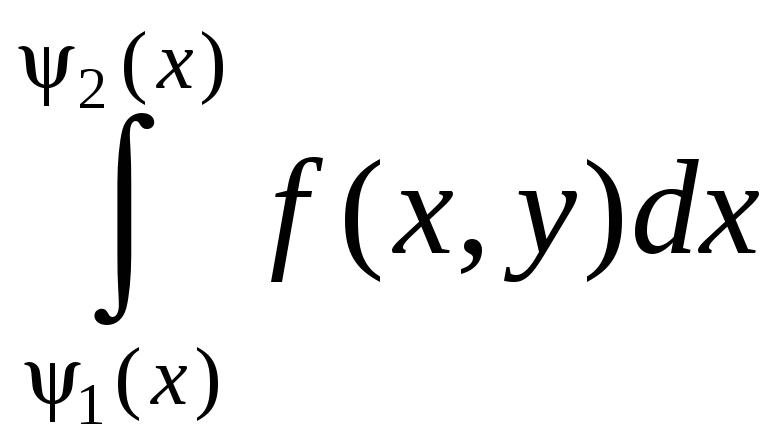, в котором у считается постоянным.

Правые части указанных формул называются повторными (или двукратными) интегралами

Y

d

с

X

Рис. 6.

В более общем случае область интегрирования путем разбиения на части сводится к основным областям.

Пример 1. Вычислить , где область ограничена линиями .

Решение. Построим область . Из рисунка видно, что она принадлежит к первому виду.

Находим

.

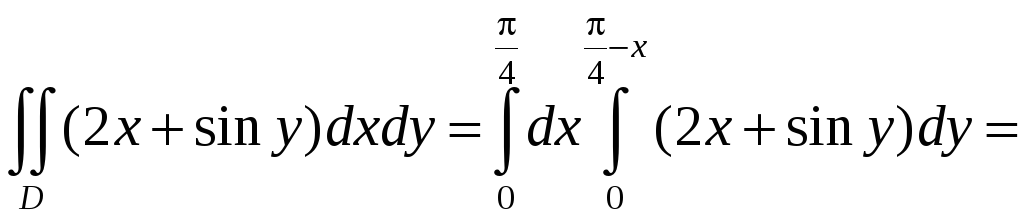
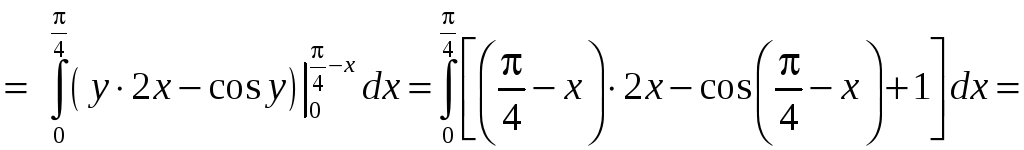
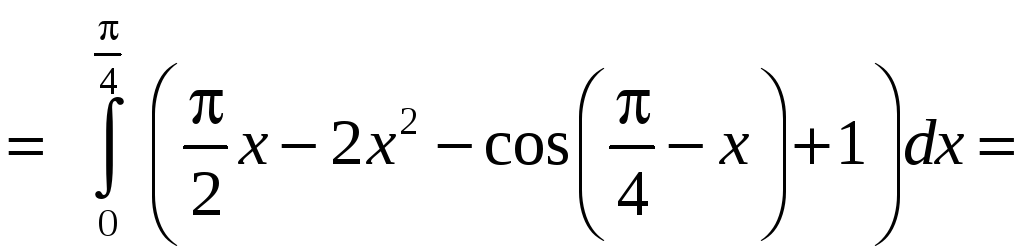
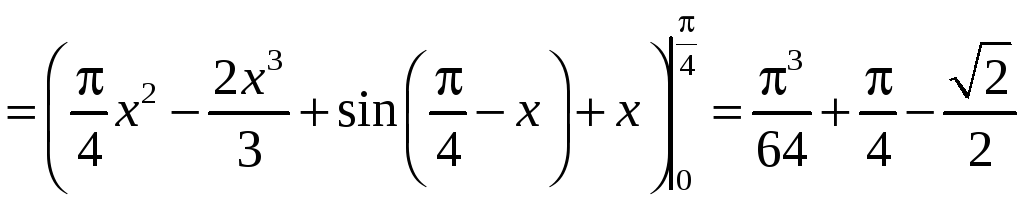Y

0 X

Рис. 7.

Пример 2. Изменить порядок интегрирования в повторном интеграле .

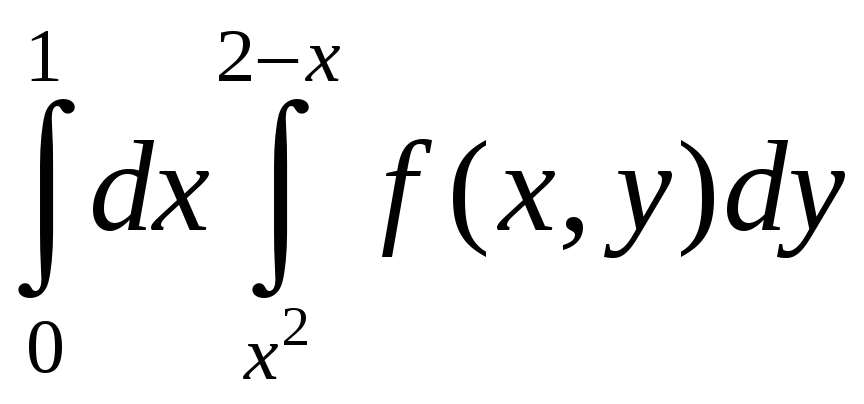Решение. Область интегрирования расположена между прямыми , ограничена снизу параболой , сверху прямой (рис. 8).

Так как правый участок границы области задан двумя линиями, то прямая разбивает ее на области и .

В результате получаем

.

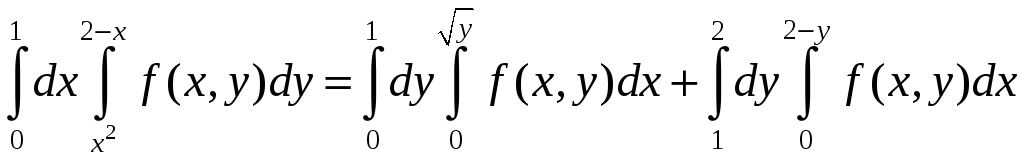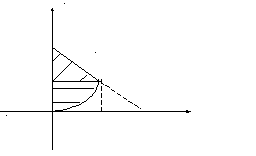
Y

2

D₂

1

D₁

0 1 2 Х

Рис. 8

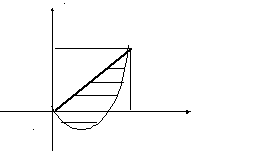
Пример 3. Вычислить площадь фигуры, ограниченной линиями .

Решение. По уравнениям границы области строим данную фигуру (рис.9). На основании свойства 3 двойных интегралов искомая площадь

.

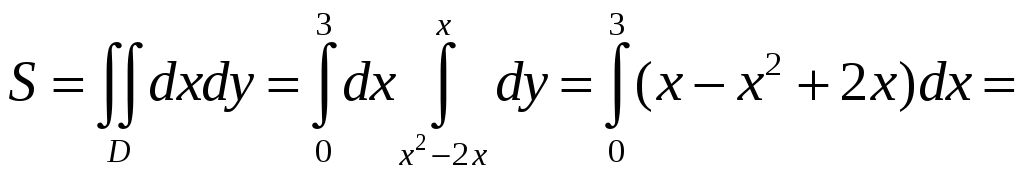
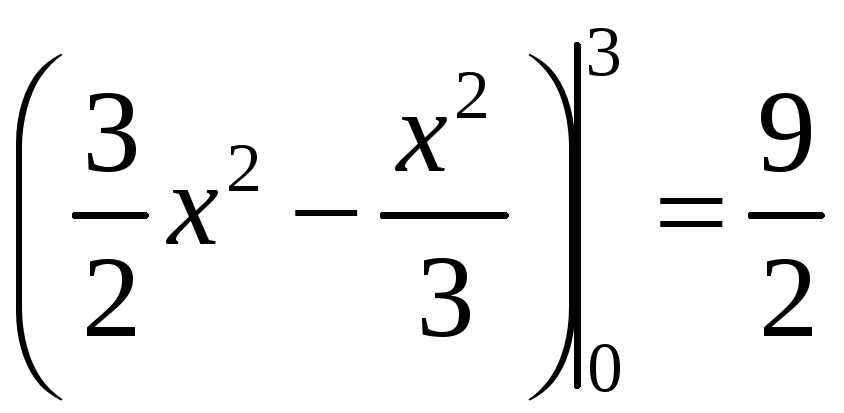Y

3

0 1 3 Х

Рис. 9.