
- •Тема 1. Неопределеный интеграл
- •1.1. Первообразная функция и неопределенный интеграл. Таблица основных интегралов
- •Свойства неопределенного интеграла
- •1.2. Основные методы интегрирования
- •Задание 1
- •Тема 2. Определеный интеграл и его приложения
- •Задание 2
- •Тема 3. Несобственные интегралы
- •Задание 3
- •Тема 4. Двойной интеграл
- •Основные свойства двойного интеграла
- •Правила вычисления двойных интегралов
- •Задание 4
- •Задание 5
- •Тема 5. Дифференциальные уравнения
- •5.1. Дифференциальные уравнения (ду). Основные понятия и определения.
- •5.2. Дифференциальные уравнения первого порядка.
- •5.3. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •5.4. Линейные дифференциальные уравнения второго порядка.
- •Задание 6
- •Задание 7
- •Задание 8
- •Тема 6. Ряды
- •6.1. Числовые ряды. Необходимый признак сходимости.
- •6.1. Достаточные признаки сходимости знакоположительных рядов.
- •1. Признаки сравнения.
- •6.3. Абсолютная и условная сходимость знакопеременных рядов.
- •6.4. Степенные ряды
- •Задание 9
- •Задание 10
- •Литература
Министерство образования Республики Беларусь
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Высшая математика № 2»
ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К КОНТРОЛЬНОЙ РАБОТЕ №2
ПО ВЫСШЕЙ МАТЕМАТИКЕ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
ЭКОНОМИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ
М и н с к 2 0 1 0
УДК 519.85 (075.8)
ББК 18.87я7
М 54
Составители: А.Д. Корзников, Л.Д. Матвеева, Н.А. Шавель
Рецензенты:
В.В. Карпук, В.В.Павлов
Настоящее издание включает в себя задания по темам «Неопределенный интеграл», «Определенный интеграл и его приложения», «несобственные интегралы», «Двойной интеграл», «Дифференциальные уравнения», «Ряды».
Каждое задание состоит из 30 контрольных вариантов. По всем темам приводятся примеры решения типовых задач.
Издание содержит список рекомендуемой литературы.
Задания и методические указания предназначены для студентов 1 курса заочного отделения экономических специальностей БНТУ. Они могут быть также полезны преподавателям, ведущим практические занятия по данному курсу.
© БНТУ, 2010
Тема 1. Неопределеный интеграл
1. Первообразная функция и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица основных интегралов.
2. Непосредственное интегрирование. Интегрирование заменой переменной. Интегрирование по частям.
3. Интегрирование рациональных дробей.
4. Интегрирование рациональных выражений, содержащих тригонометрические функции.
5. Интегрирование некоторых иррациональных функций.
1.1. Первообразная функция и неопределенный интеграл. Таблица основных интегралов
Первообразной
функцией
для функции
![]() называется такая функция
называется такая функция
![]() ,
производная которой равна данной
функции, т.е.
,
производная которой равна данной
функции, т.е.
![]() .
.
Неопределенным
интегралом от
непрерывной функции
![]() называется совокупность всех первообразных
функций
называется совокупность всех первообразных
функций
![]() :
:
![]() ,
,
где
![]() .
.
Свойства неопределенного интеграла
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() .
.
Таблица основных неопределенных интегралов
-
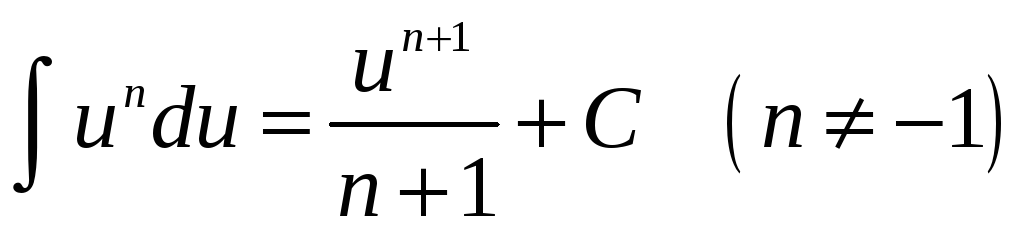 ;
; -
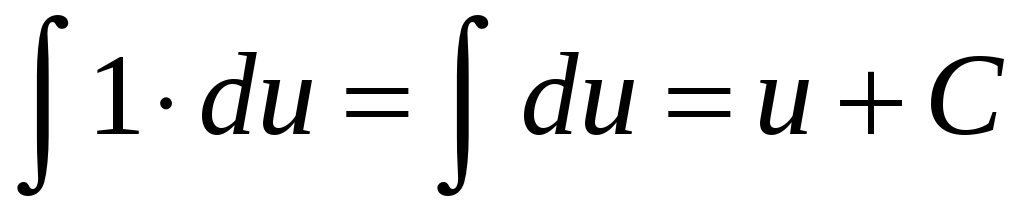 ;
; -
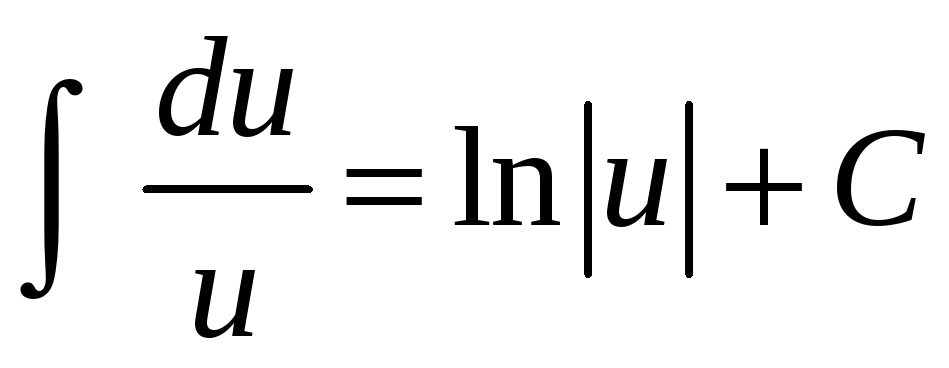 ;
; -
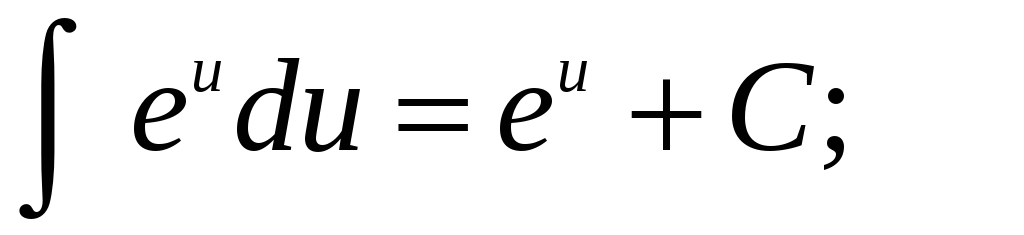
-
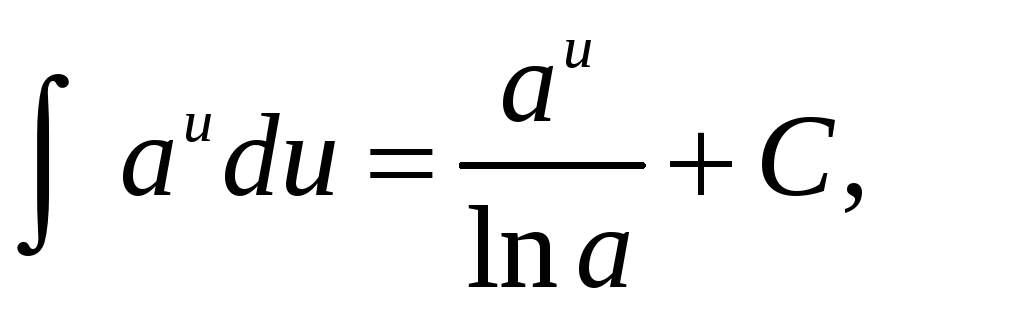
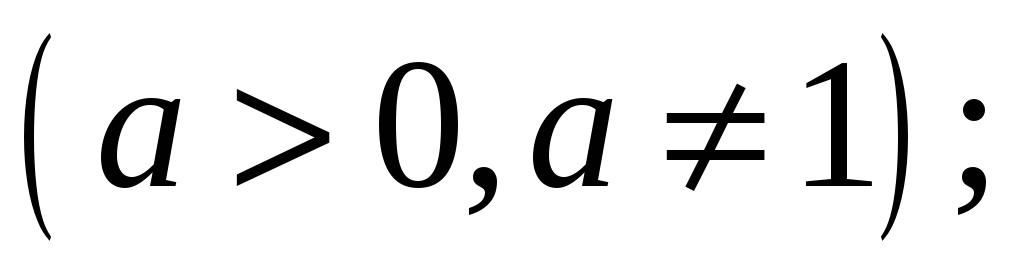
-
 ;
; -
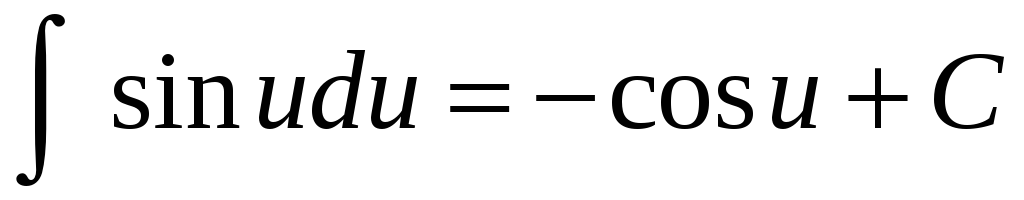 ;
; -
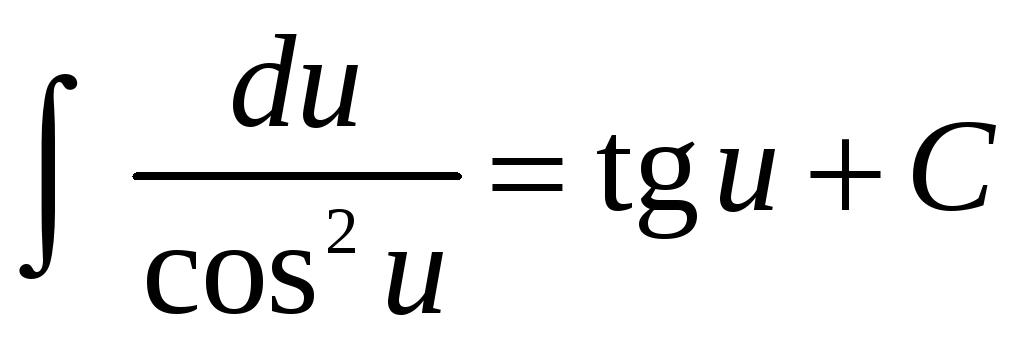 ;
; -
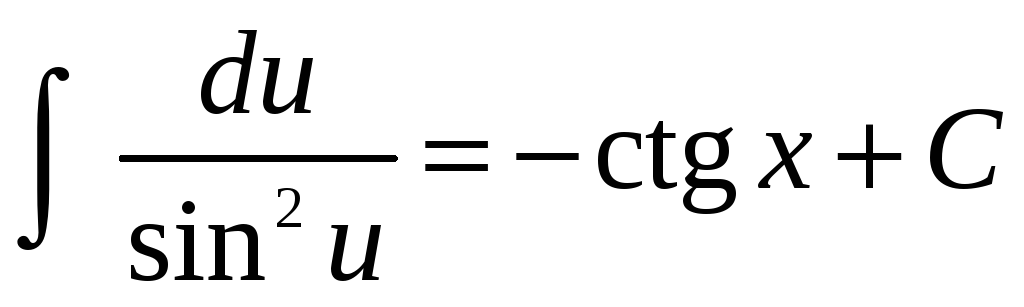 ;
; -
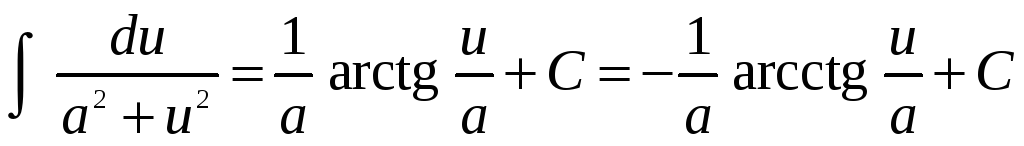 ,
,
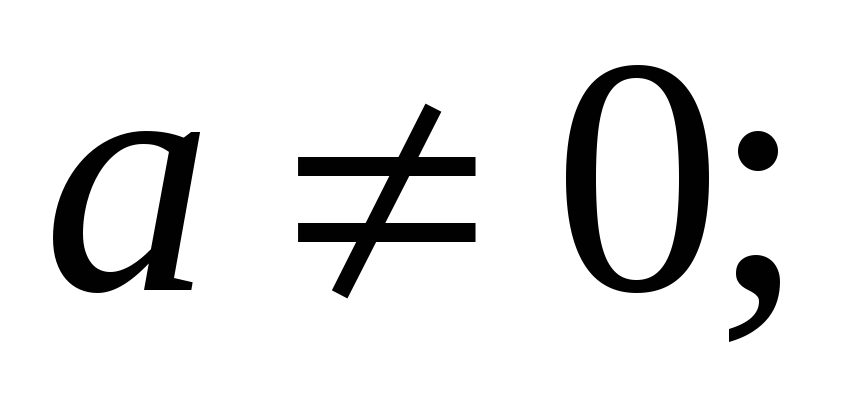
-
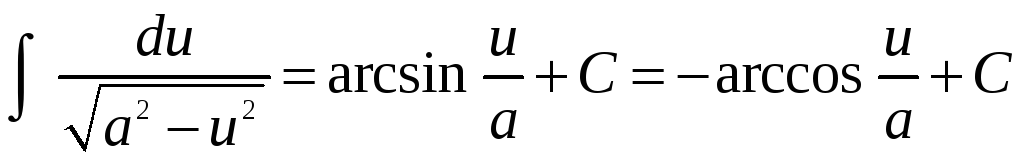 ;
; -
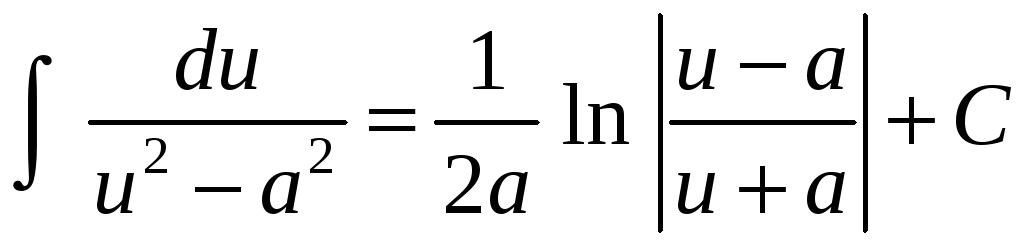 ;
; -
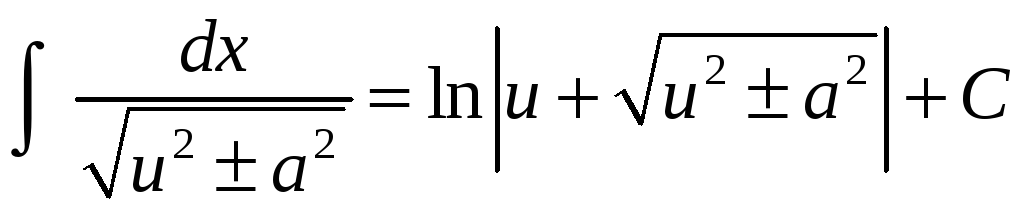 ;
; -
 .
.
1.2. Основные методы интегрирования
а) Метод непосредственного интегрирования основан на свойствах 3, 4 и таблице неопределенных интегралов.
Пример 1.1.
Вычислить
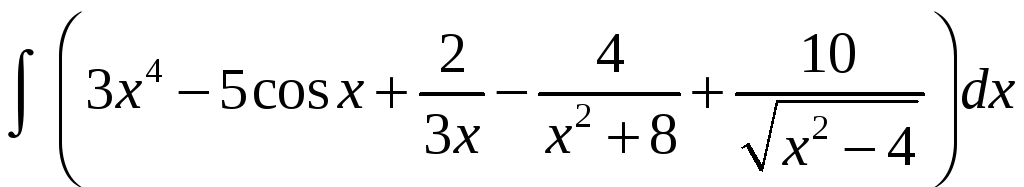 .
.
Решение. Применяя свойства 3, 4 и таблицу, получаем:
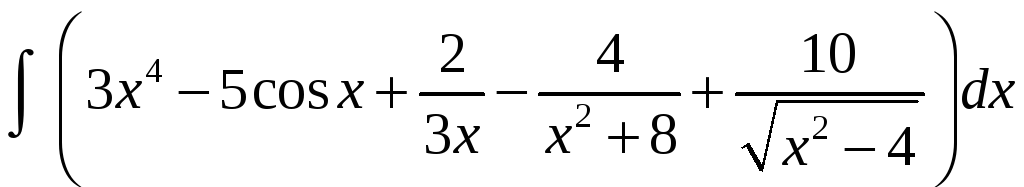 =
=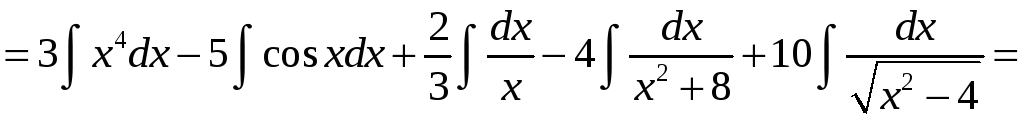
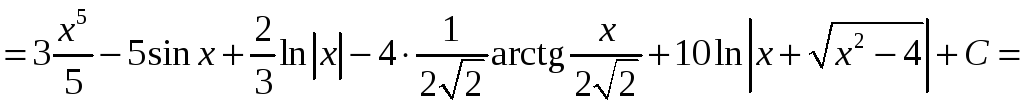
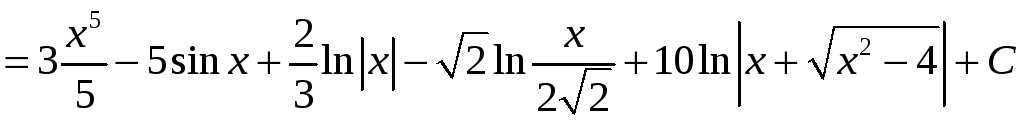 .
.
б) Метод подстановки основан на формуле:
![]()
Пример 1.2.
Вычислить
![]() .
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Сделаем замену
.
Сделаем замену
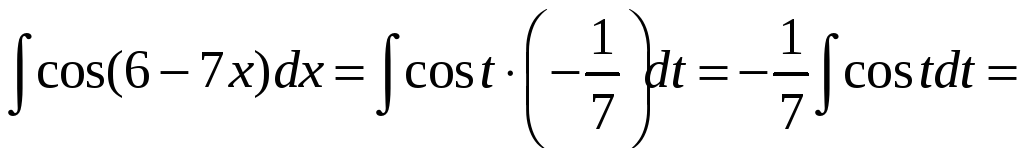
![]() .
.
Пример 1.3.
Вычислить
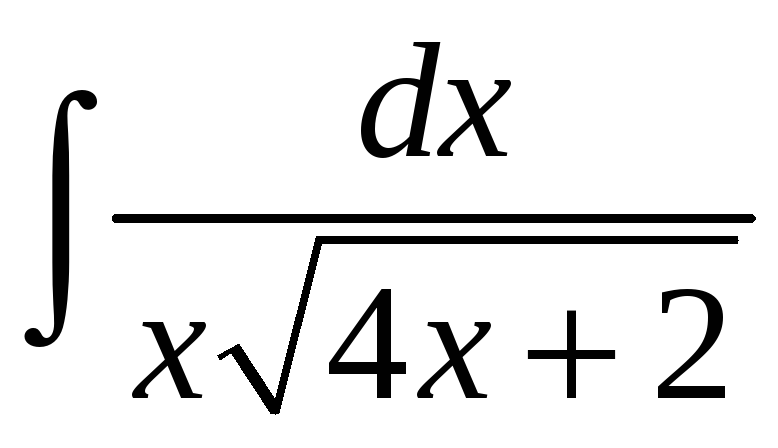 .
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Сделаем замену
.
Сделаем замену
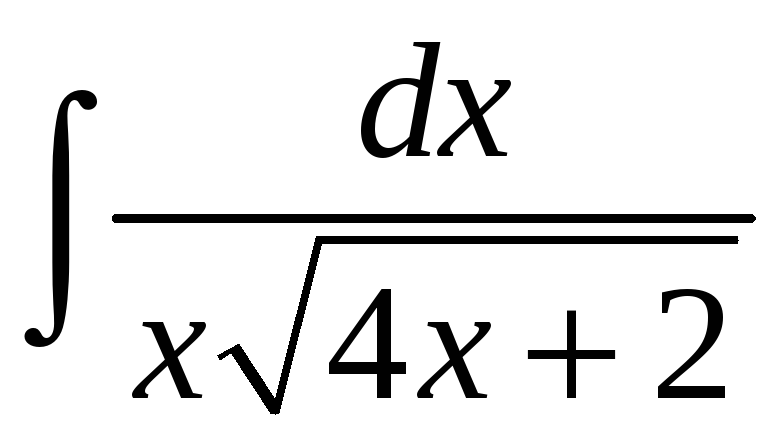 =
=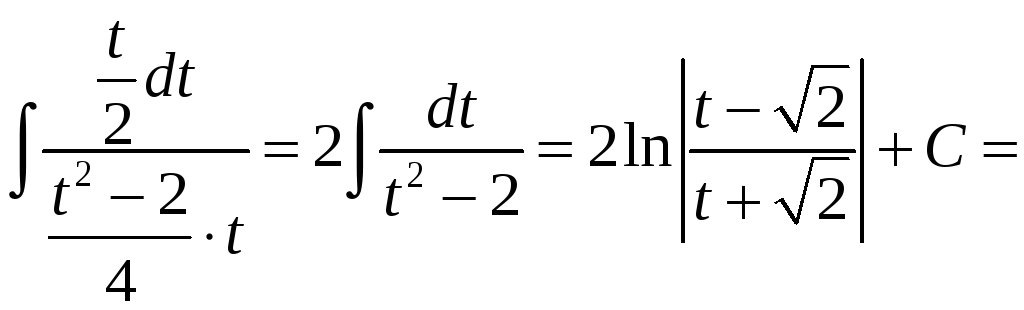
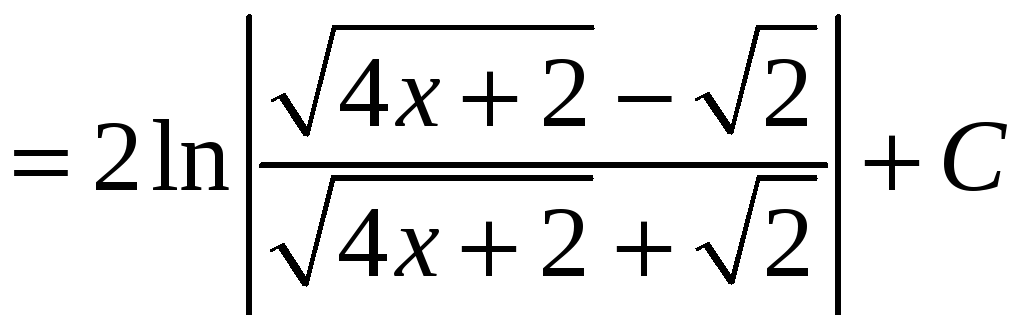 .
.
в) Интегрирование по частям выполняется по формуле:
![]() ,
,
полученной из
равенства
![]() .
.
Пример 1.4.
Вычислить
![]() .
.
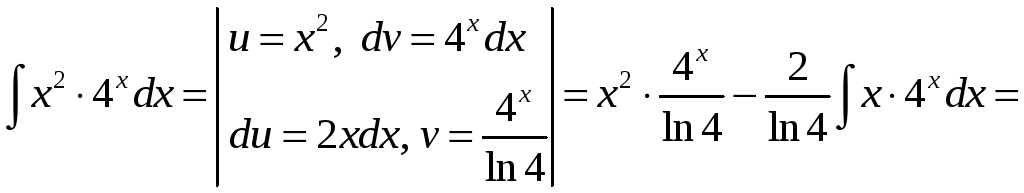
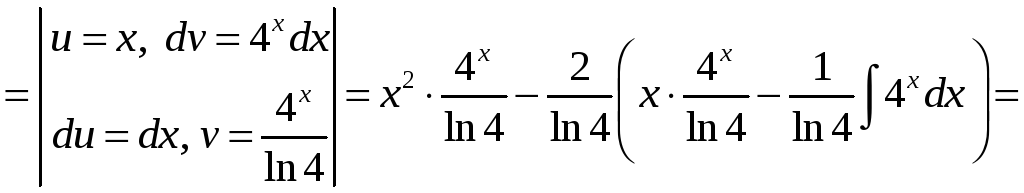
![]() .
.
Пример 1.5.
Вычислить
![]() .
.
![]()
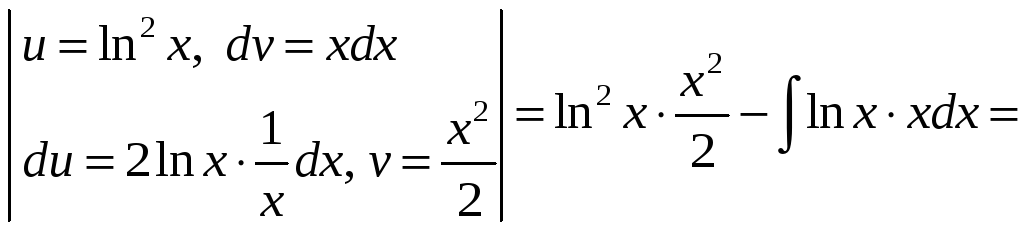
=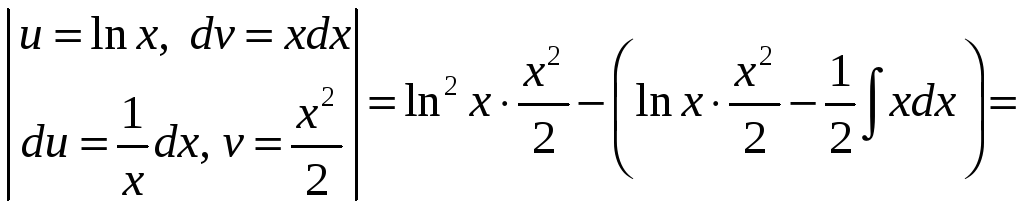
![]() .
.
Методы интегрирования основных классов интегралов можно найти в литературе [1], [2].
Задание 1
Найти неопределенные интегралы.
1.1 а)
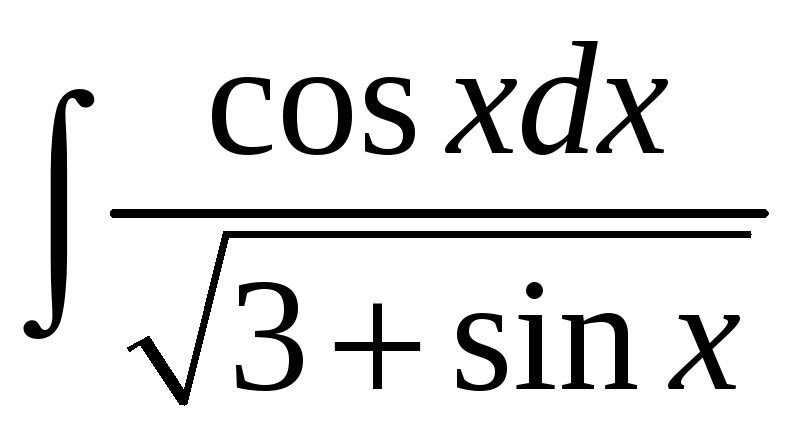 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
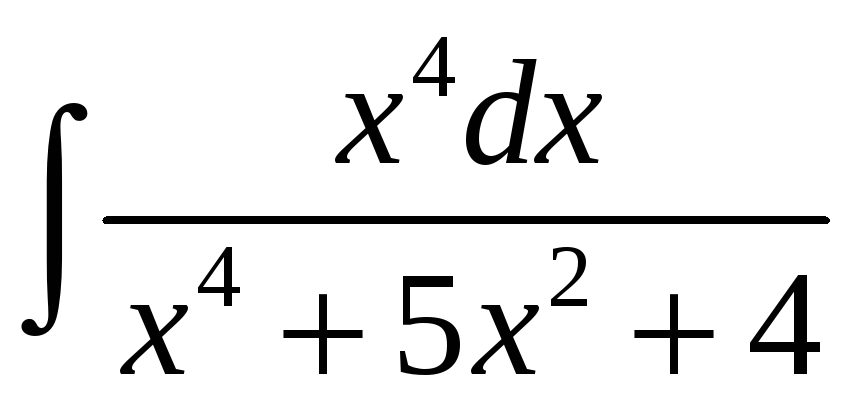 ; д)
; д)
![]() ;. е)
;. е)
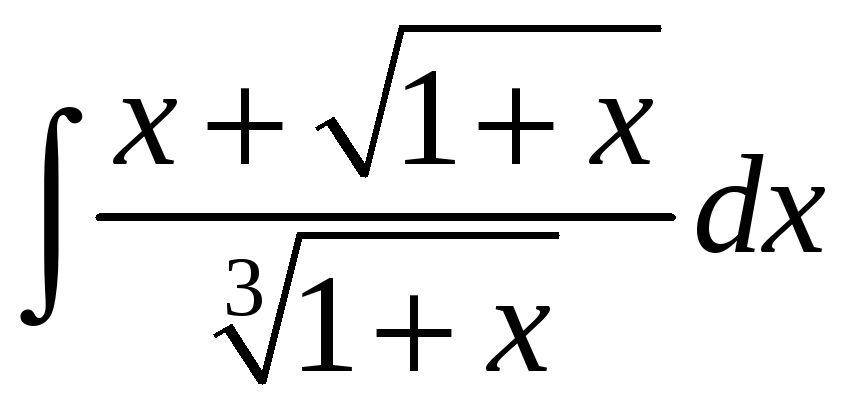 .
.
1.2 а)
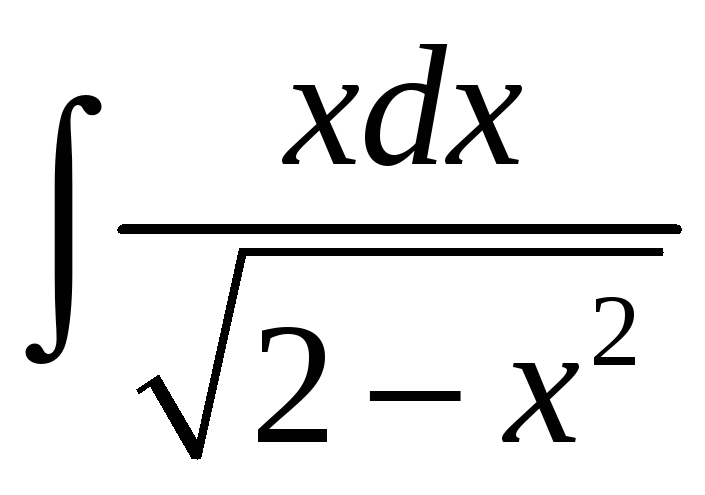 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
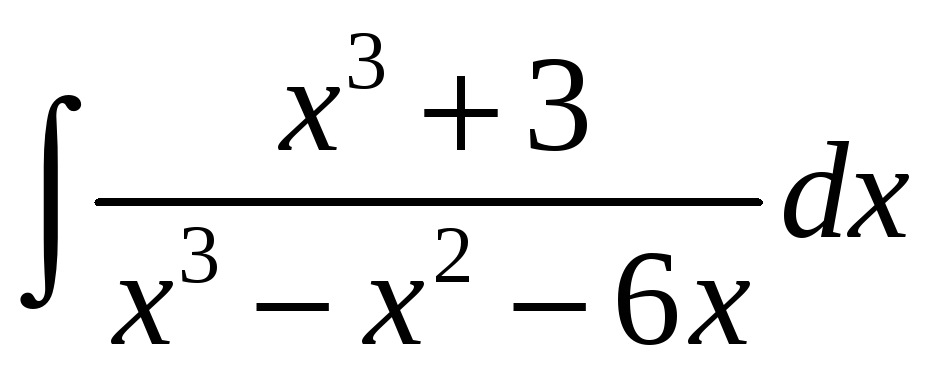 ; д)
; д)
![]() ;. е)
;. е)
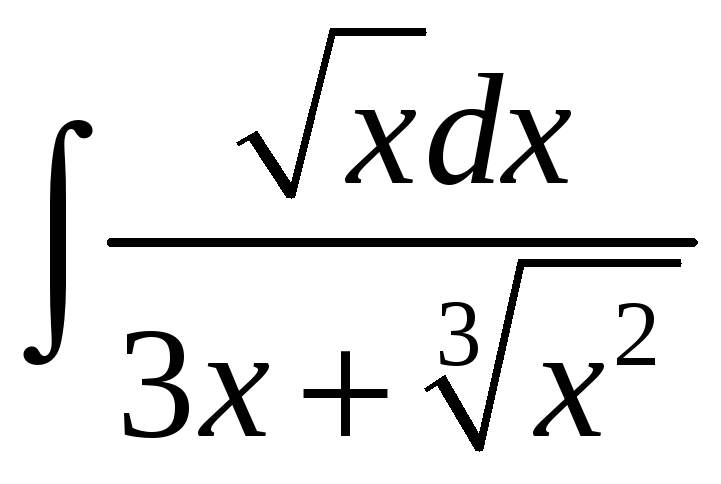 .
.
1.3 а)
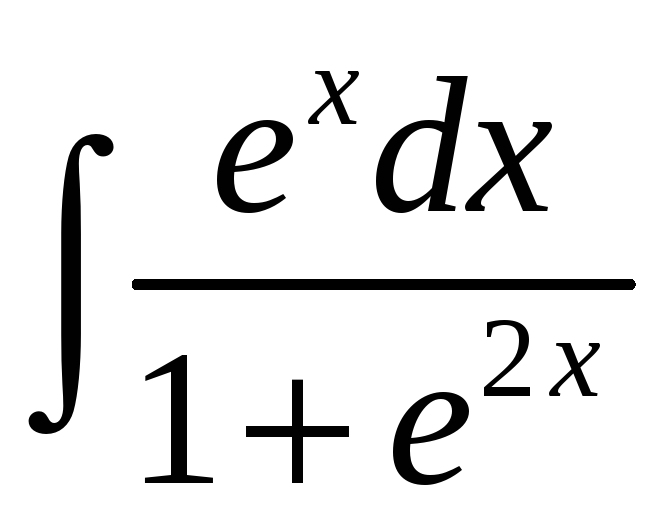 ; б)
; б)
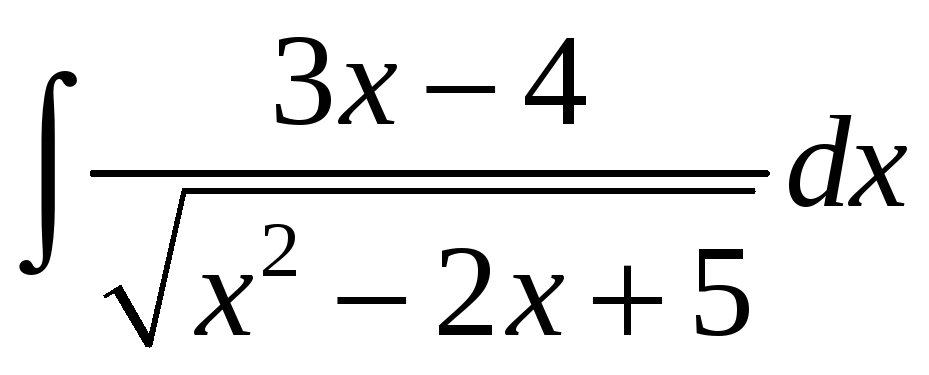 ;. в)
;. в)
![]() ;
;
г)
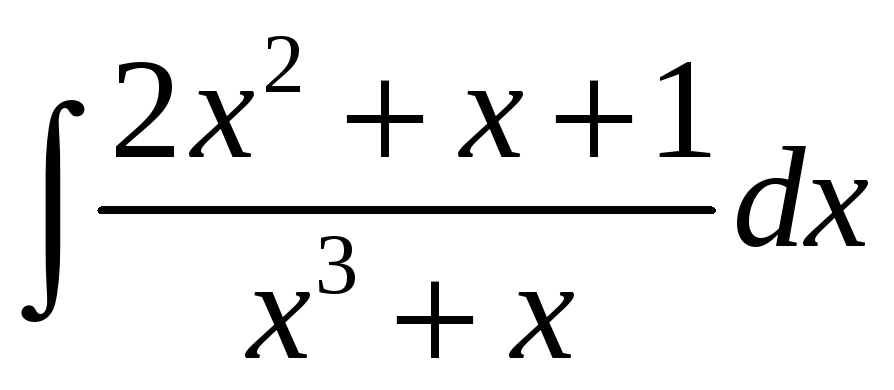 ; д)
; д)
![]() ;. е)
;. е)
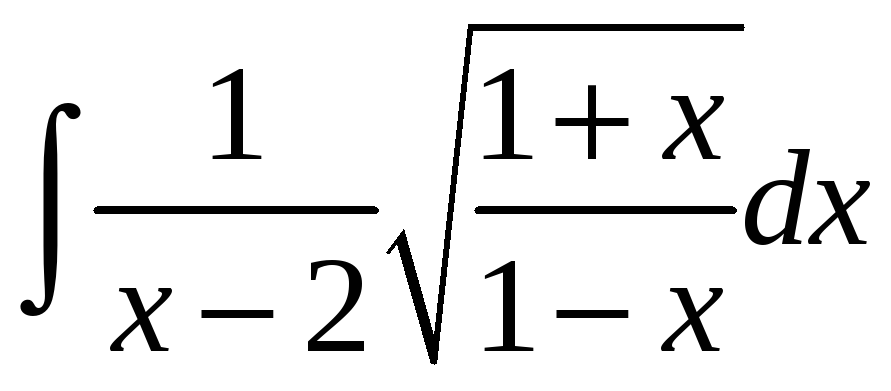 .
.
1.4 a)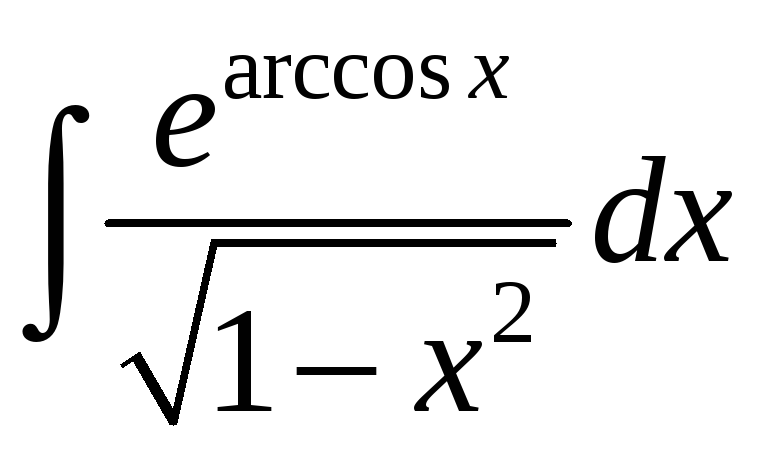 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
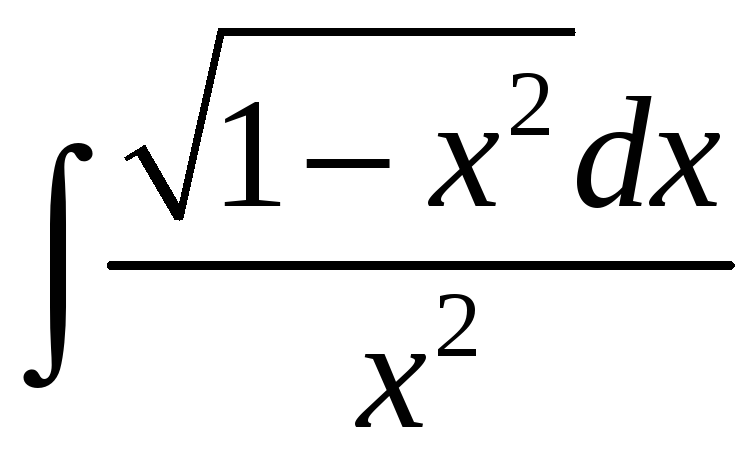 .
.
1.5 а)
![]() ; б)
; б)
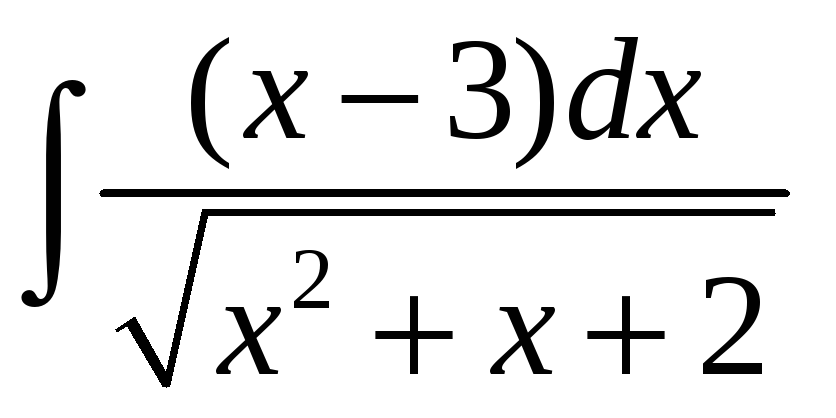 ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
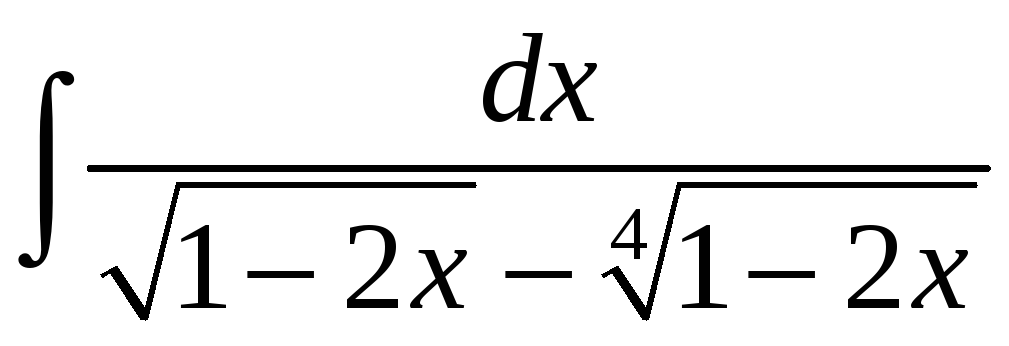 ;. е)
;. е)
![]() .
.
1.6 а)
![]() ; б)
; б)
 ;. в)
;. в)
![]() ;
;
г)
 ; д)
; д)
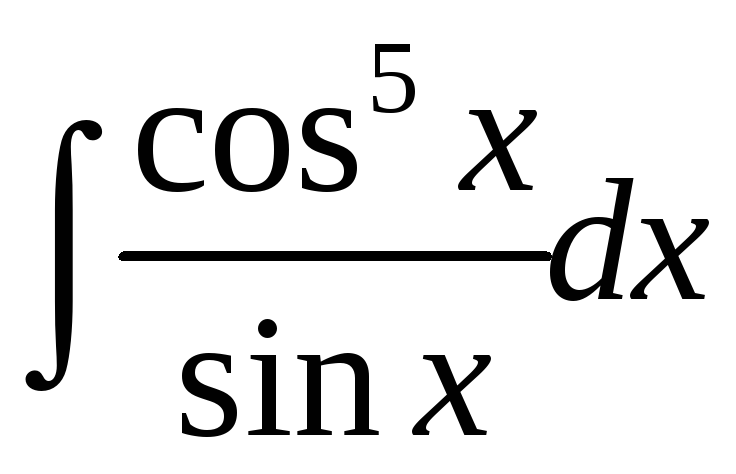 ;. е)
;. е)
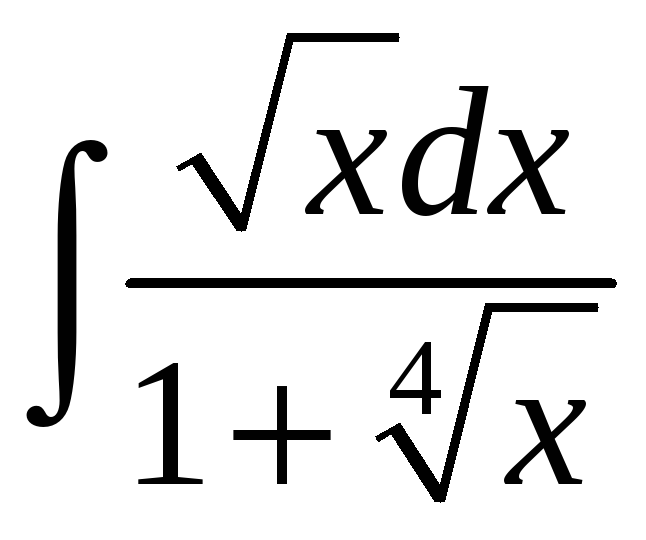 .
.
1.7
а)
![]() ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
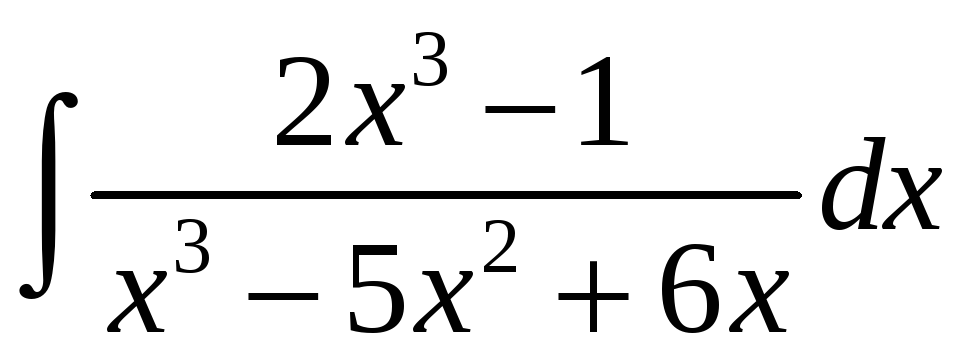 ; д)
; д)
![]() ;. е)
;. е)
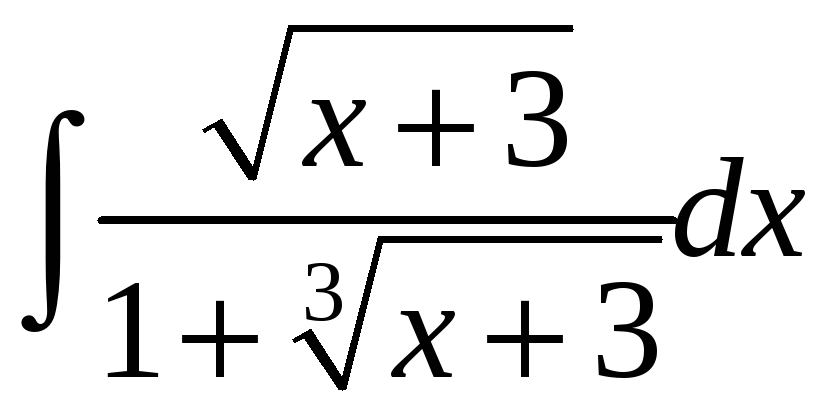 .
.
1.8
а)
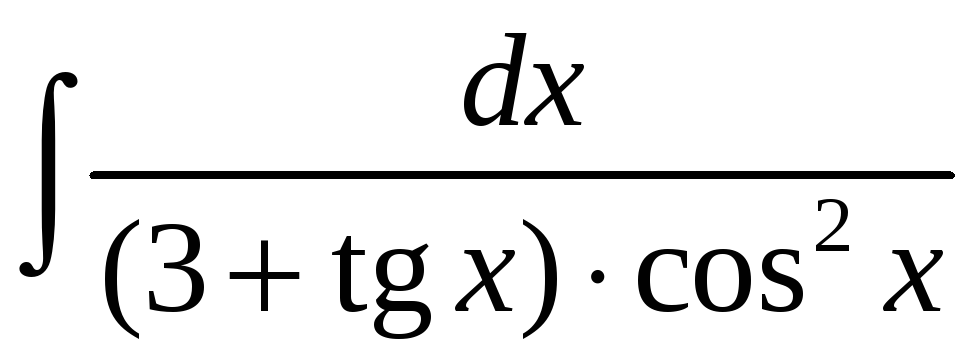 ; б)
; б)
 ;. в)
;. в)
![]() ;
;
г)
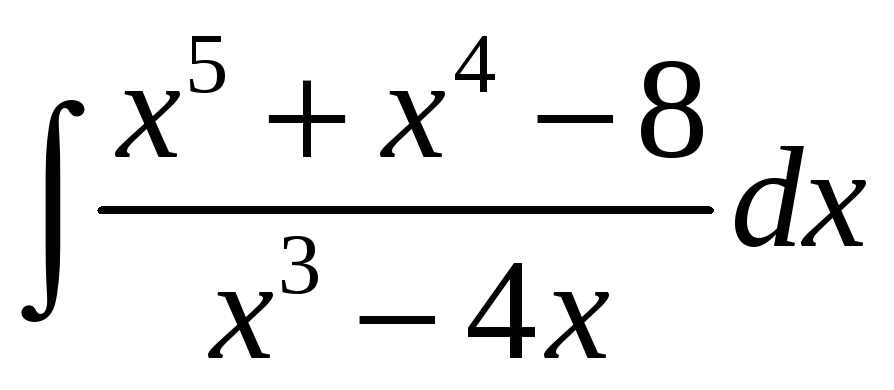 ; д)
; д)
![]() ;. е)
;. е)
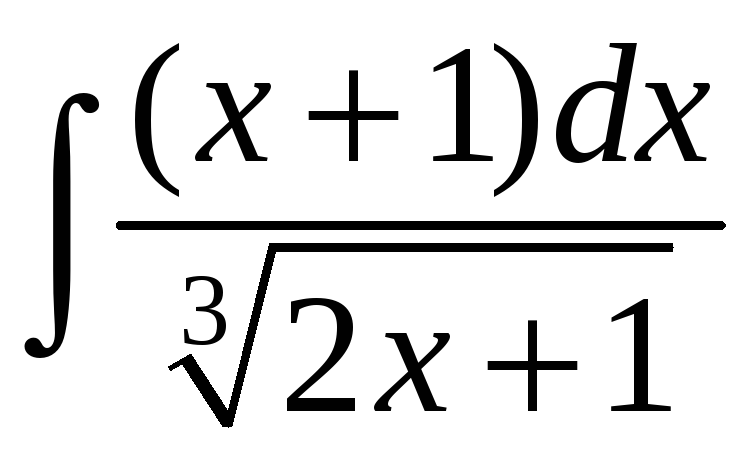 .
.
1.9
а)
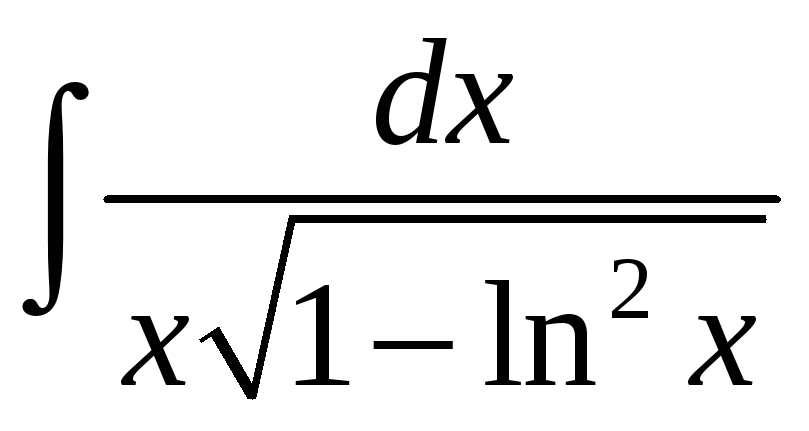 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
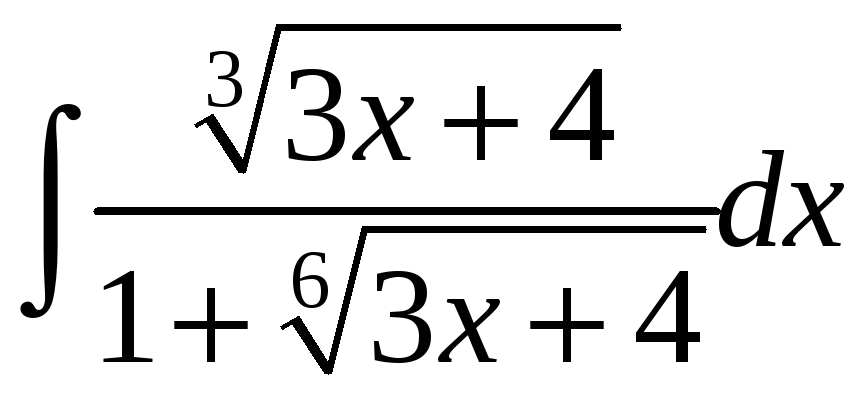 .
.
1.10
а)
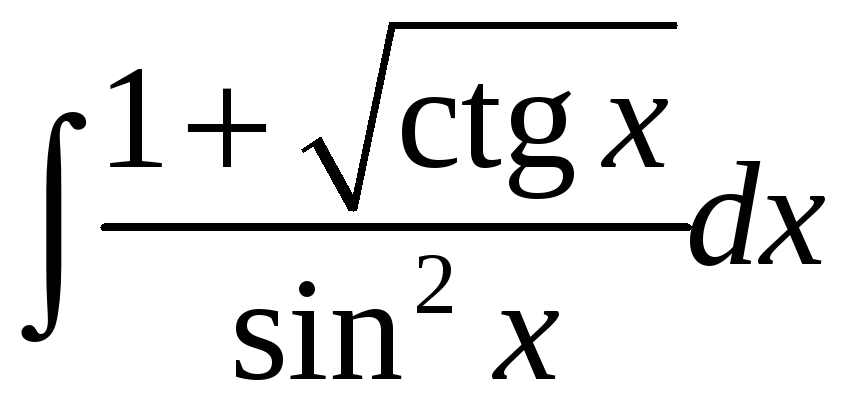 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
![]() .
.
1.11
а)
![]() ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
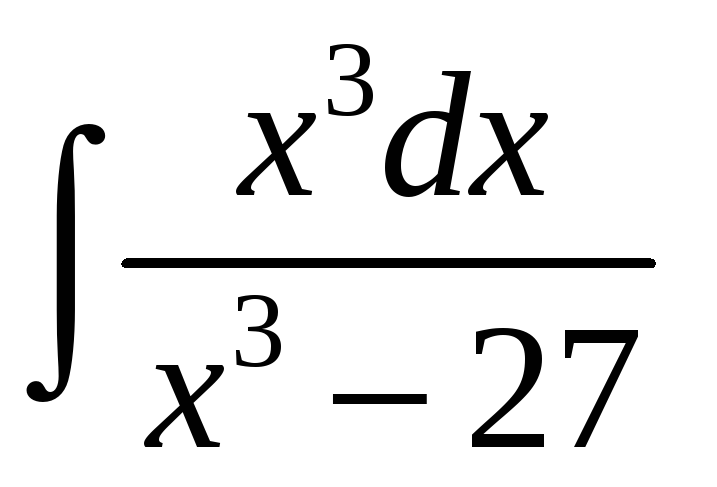 ; д)
; д)
![]() ;. е)
;. е)
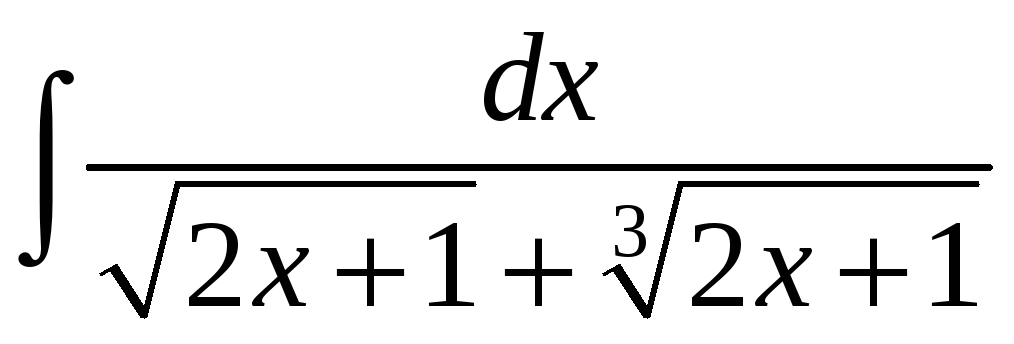 .
.
1.12 а)
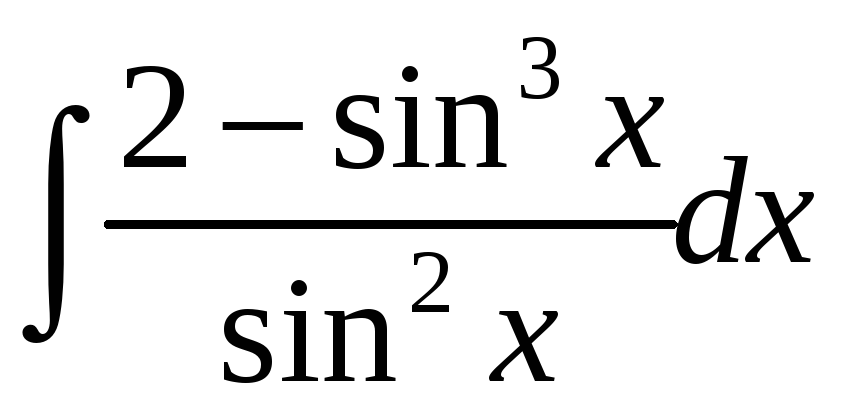 ; б)
; б)
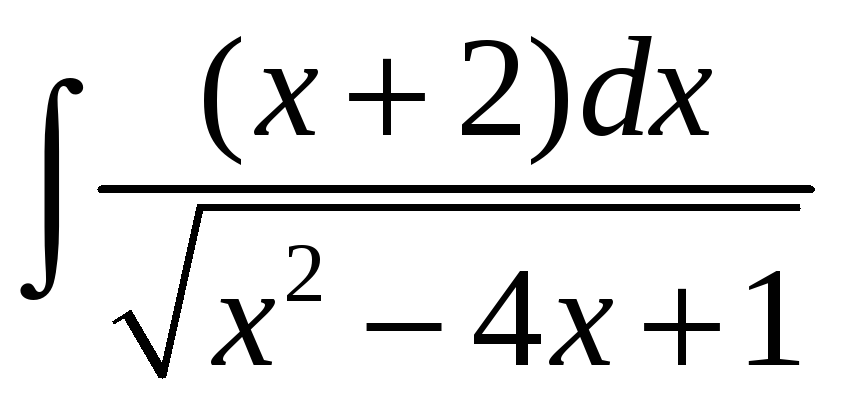 ;. в)
;. в)
![]() ;
;
г)
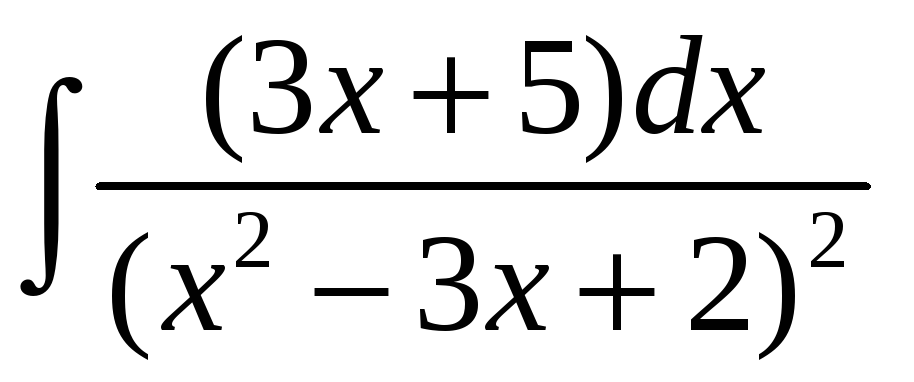 ; д)
; д)
![]() ;. е)
;. е)
![]() .
.
1.13
а)
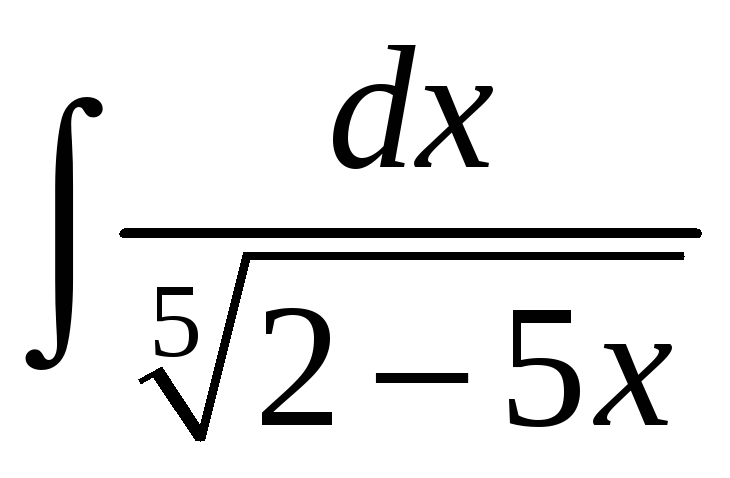 ; б)
; б)
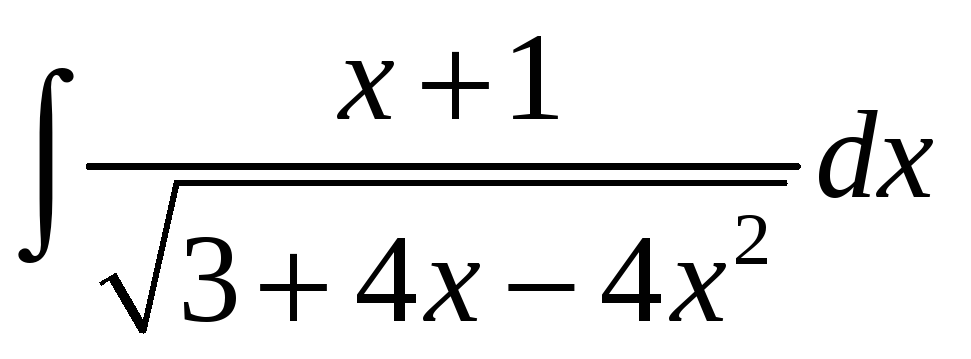 ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
 .
.
1.14 а)
![]() ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
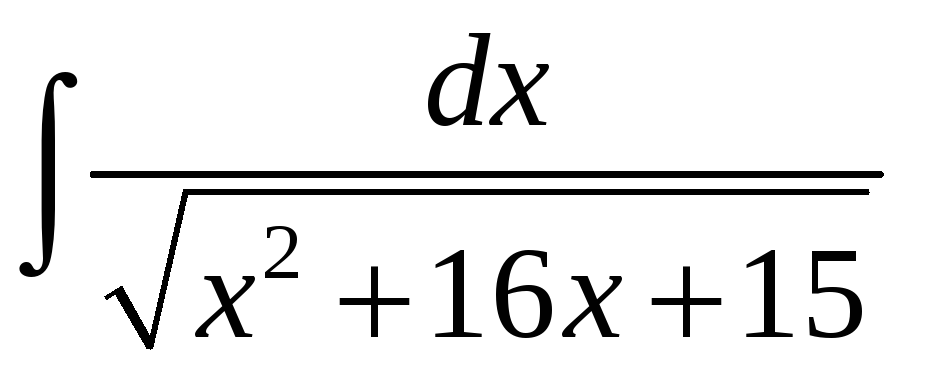 ; д)
; д)
![]() ;. е)
;. е)
![]() .
.
1.15
а)
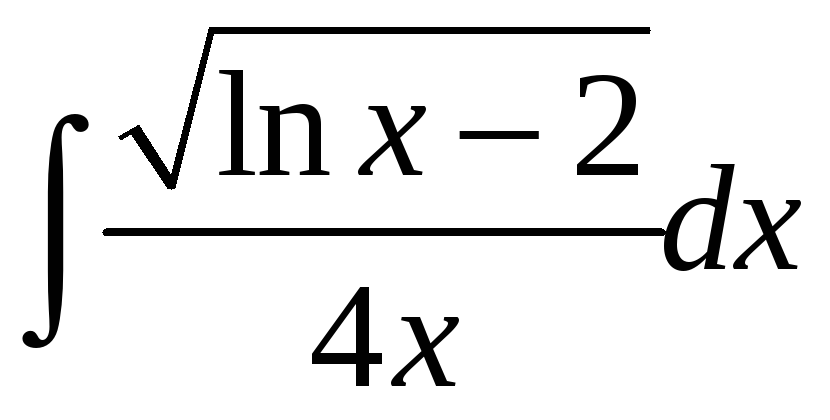 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
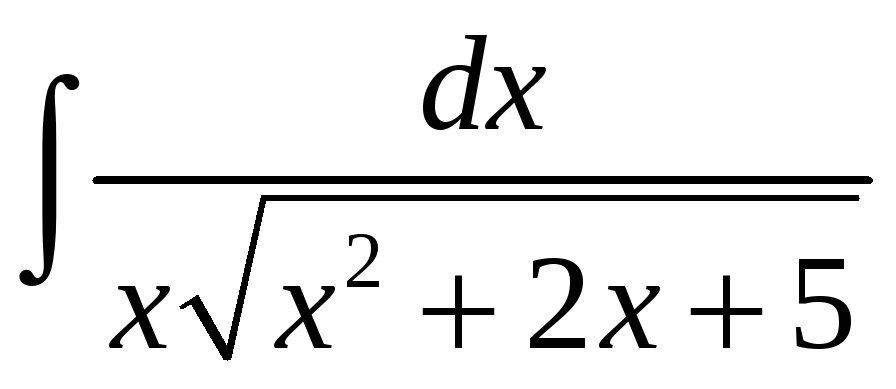 .
.
1.16
а)
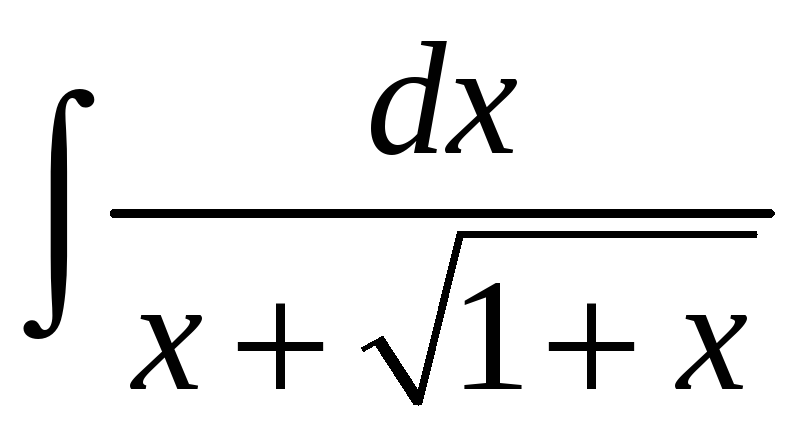 ; б)
; б)
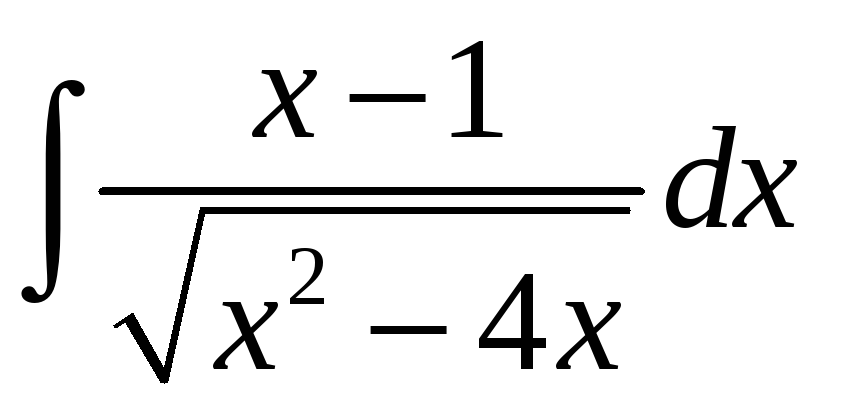 ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
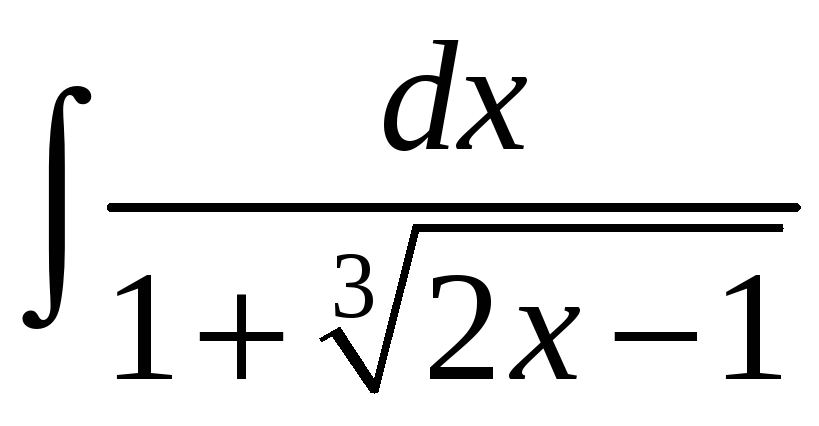 .
.
1.17
а)
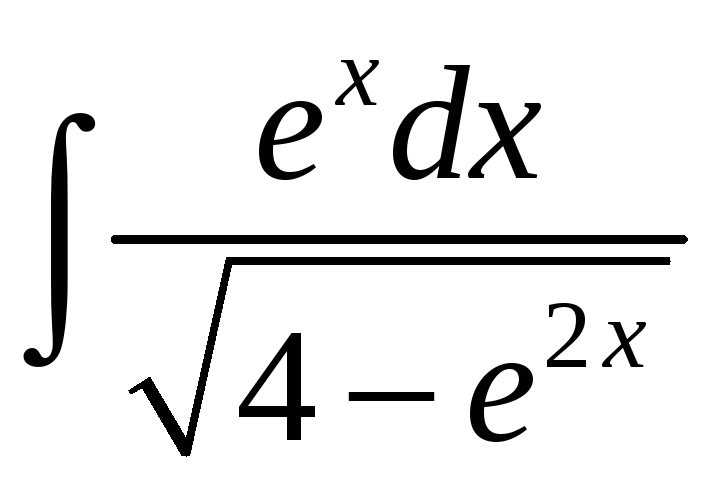 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
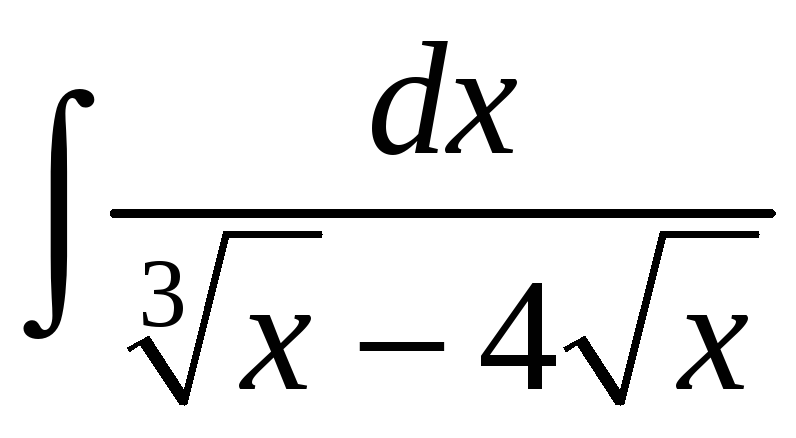 .
.
1.18
а)
![]() ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
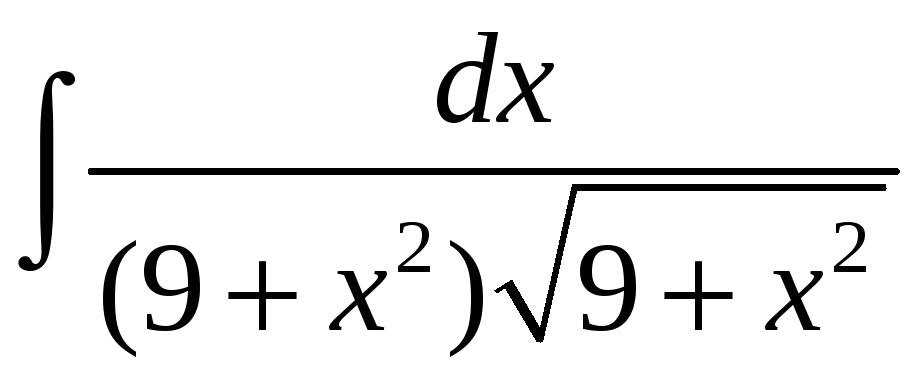 .
.
1.19 а)
![]() ; б)
; б)
 ;. в)
;. в)
![]() ;
;
г)
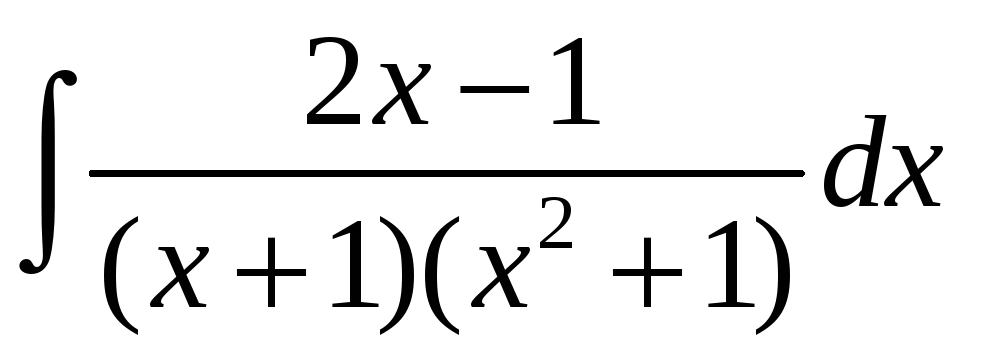 ; д)
; д)
![]() ;. е)
;. е)
![]() .
.
1.20
а)
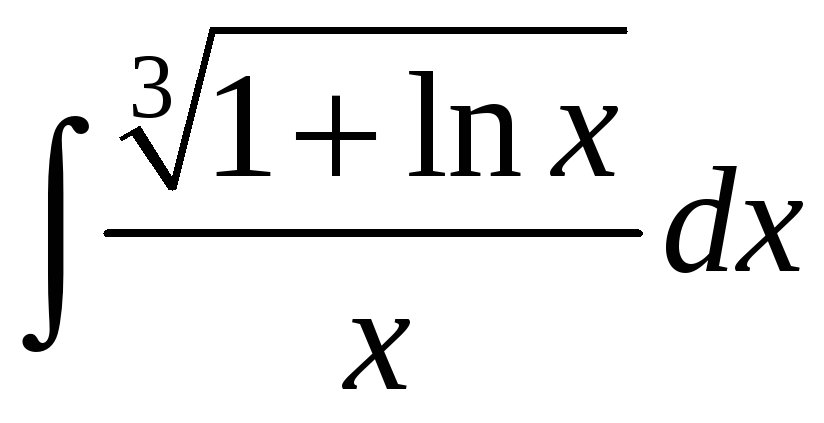 ; б)
; б)
 ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
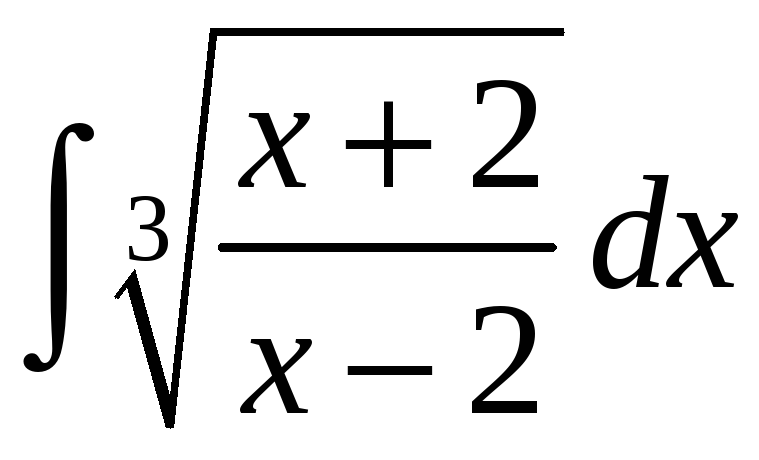 .
.
1.21
а)
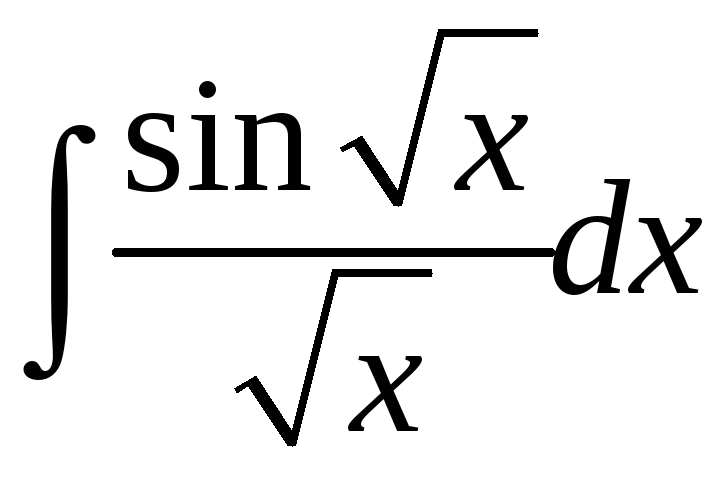 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
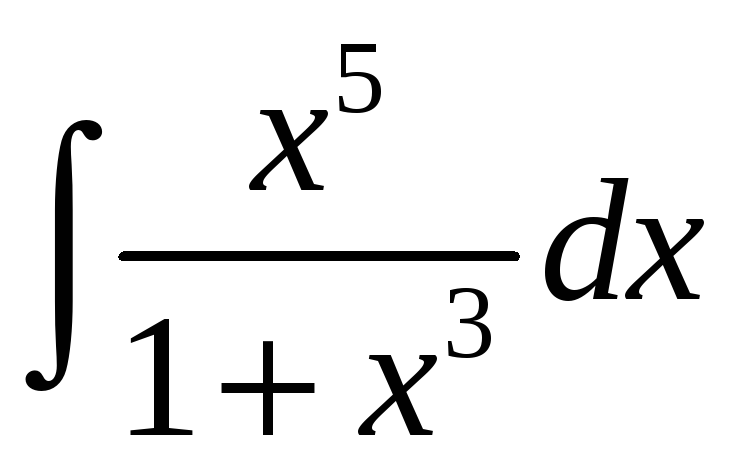 ; д)
; д)
![]() ;. е)
;. е)
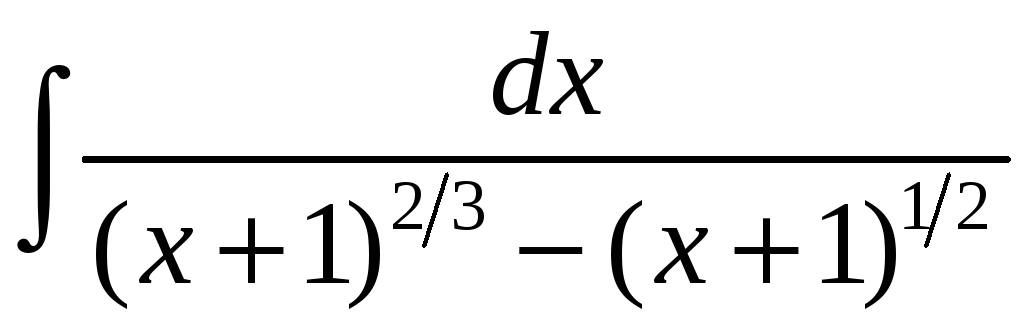 .
.
1.22
а)
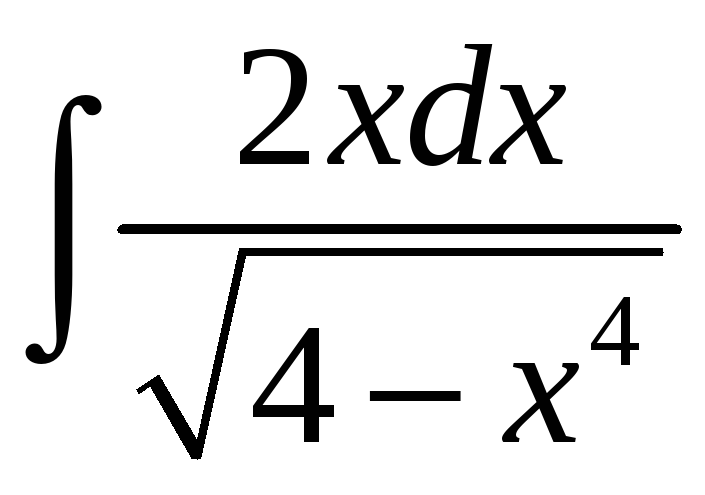 ; б)
; б)
 ;. в)
;. в)
![]() ;
;
г)
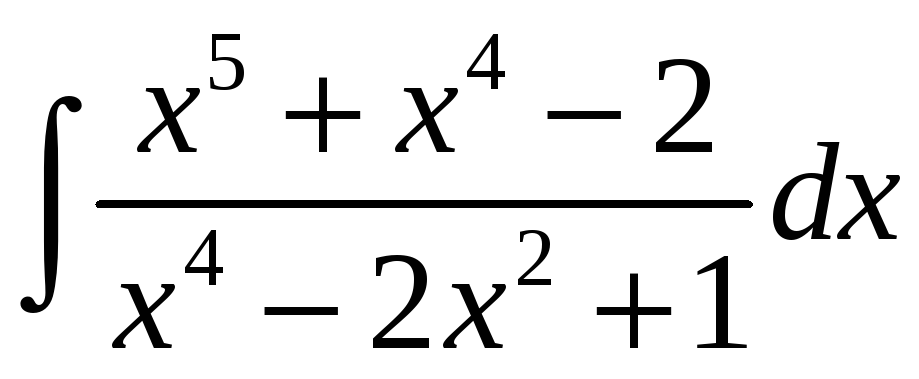 ; д)
; д)
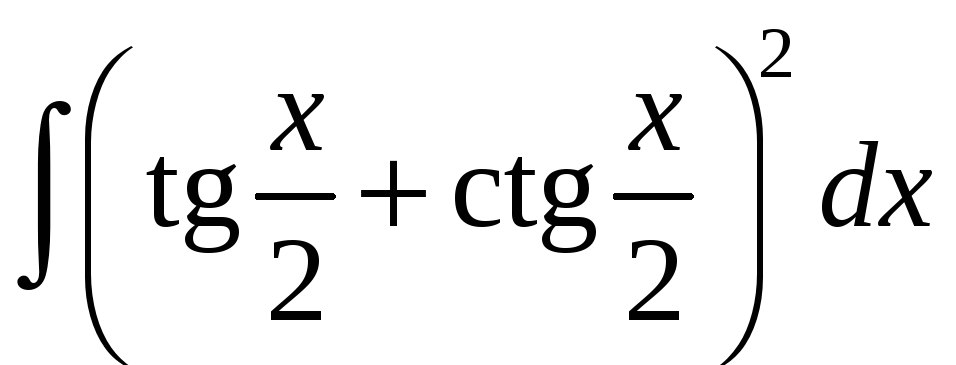 ;. е)
;. е)
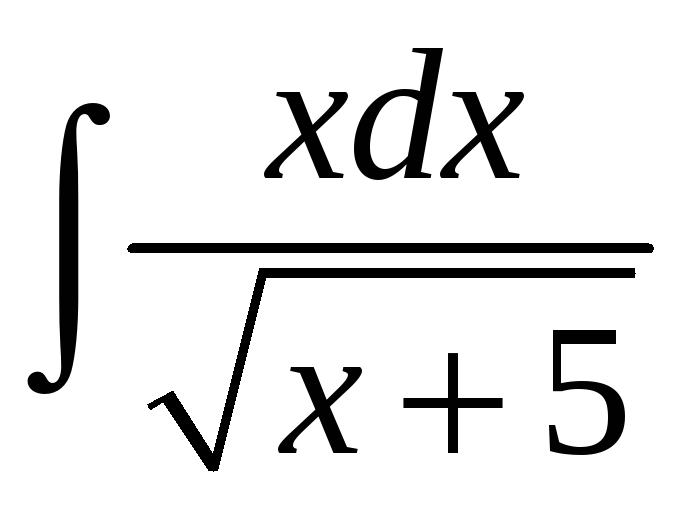 .
.
1.23
а)
![]() ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
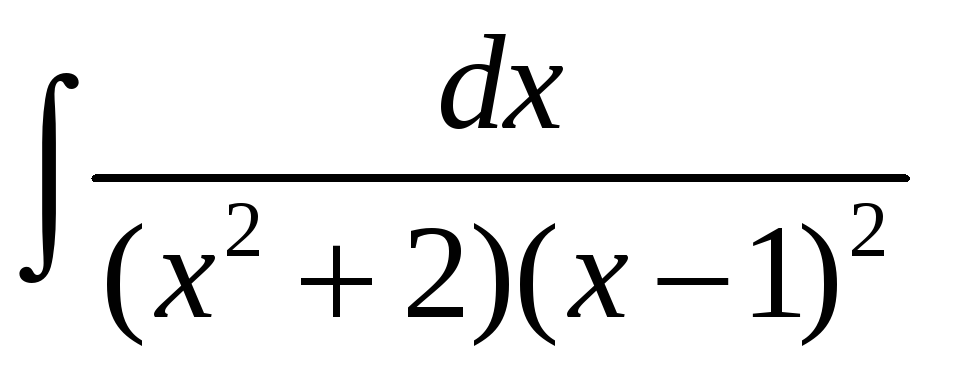 ; д)
; д)
![]() ;. е)
;. е)
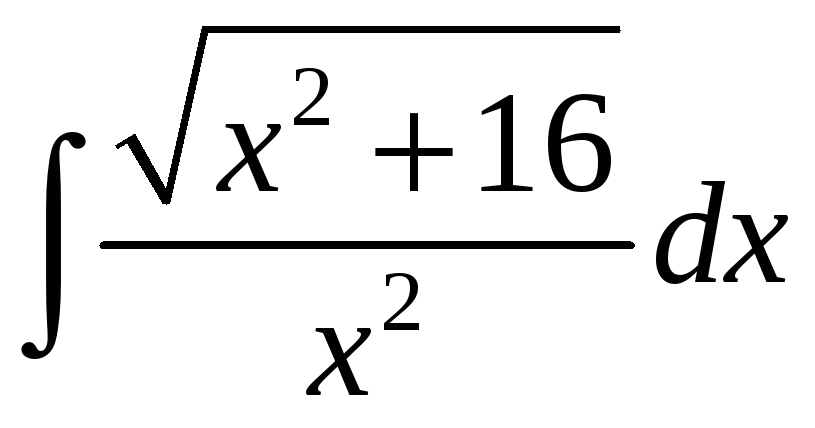 .
.
1.24 а)
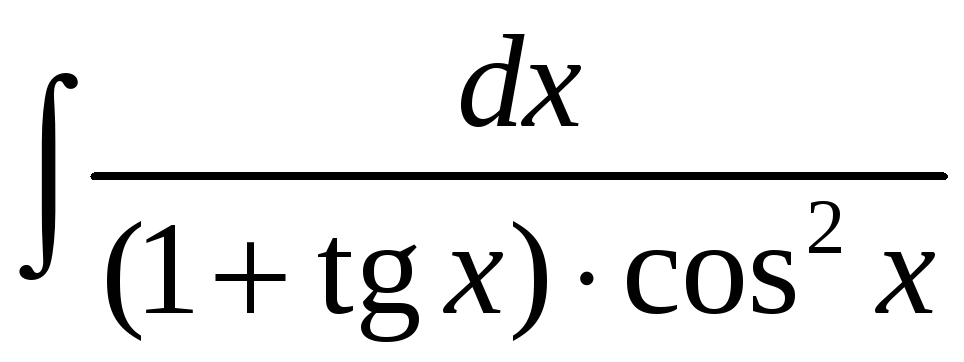 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
 .
.
1.25 а)
![]() ; б)
; б)
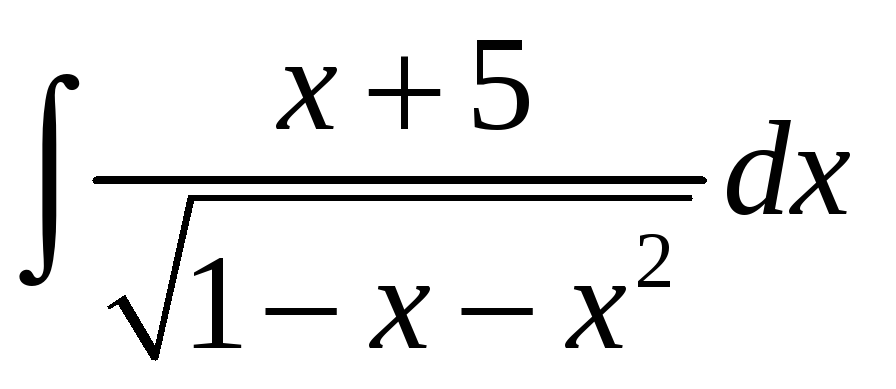 ;. в)
;. в)
![]() ;
;
г)
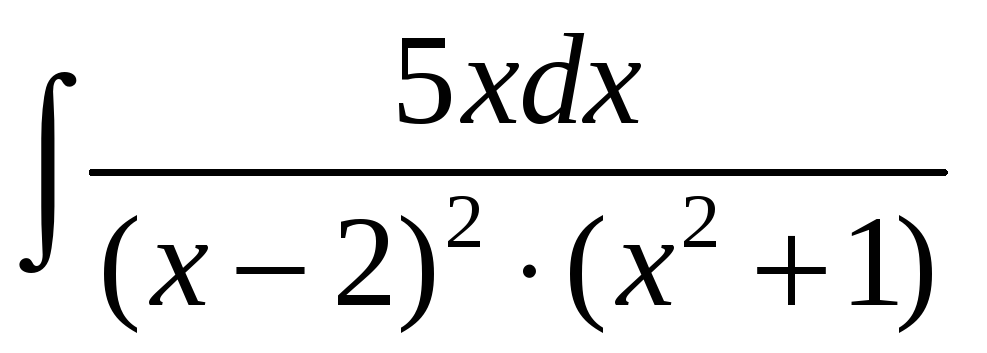 ; д)
; д)
![]() ;. е)
;. е)
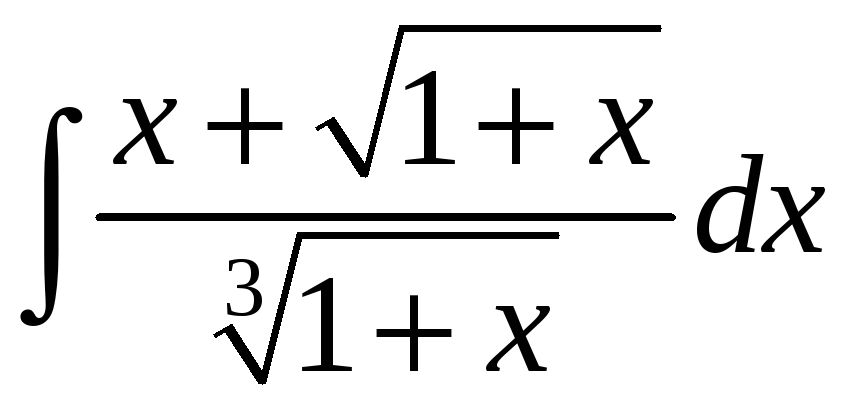 .
.
1.26
а)
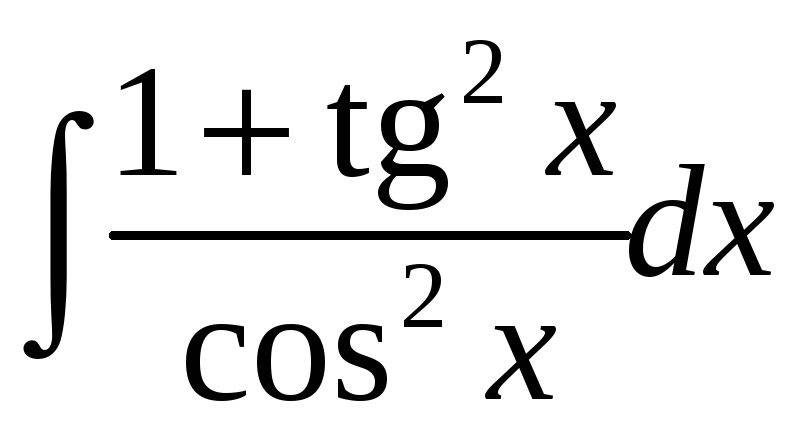 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
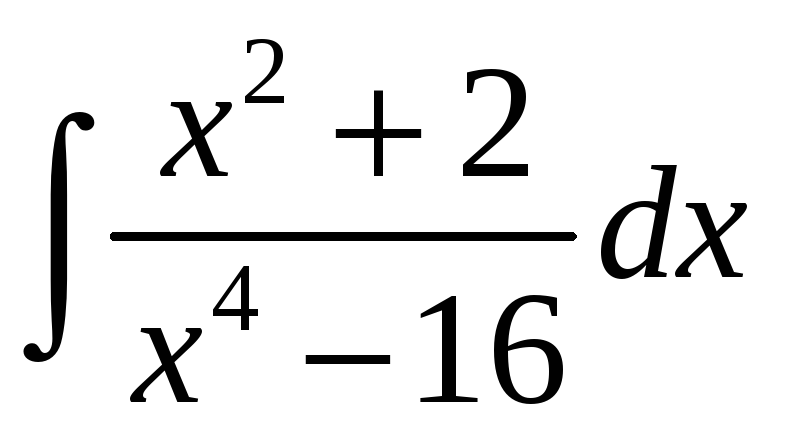 ; д)
; д)
![]() ;. е)
;. е)
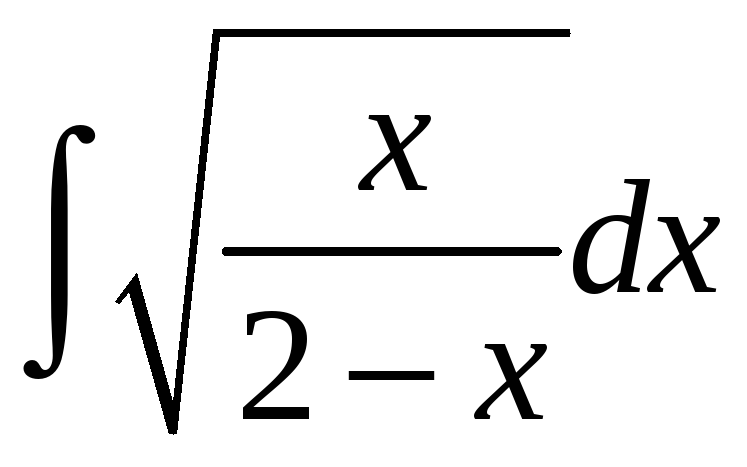 .
.
1.27
а)
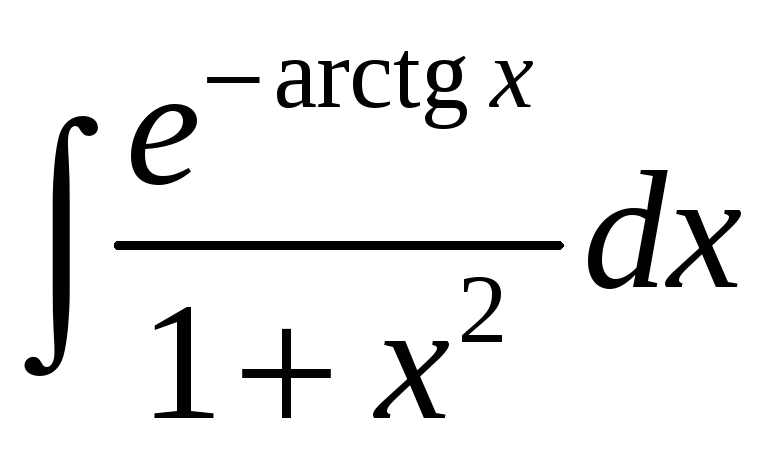 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
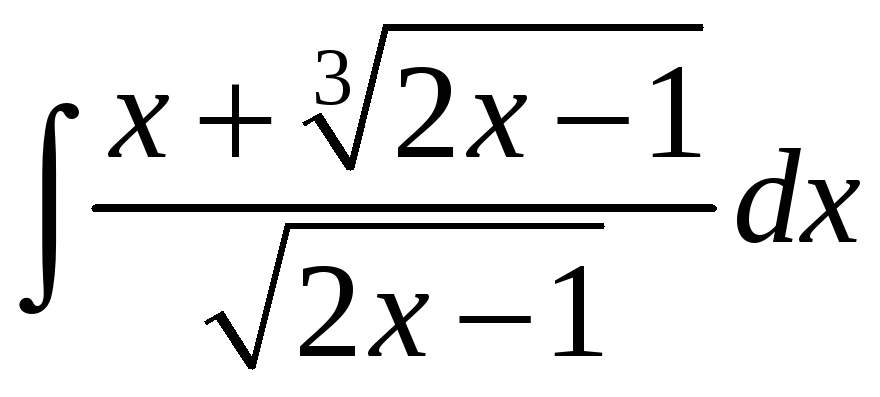 .
.
1.28
а)
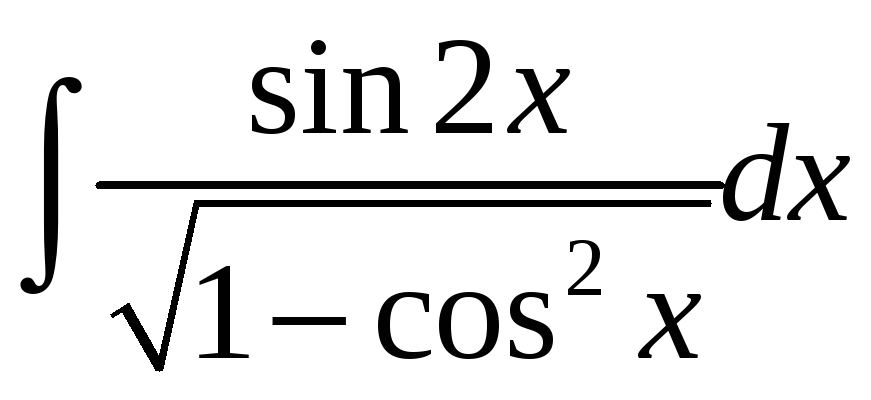 ; б)
; б)
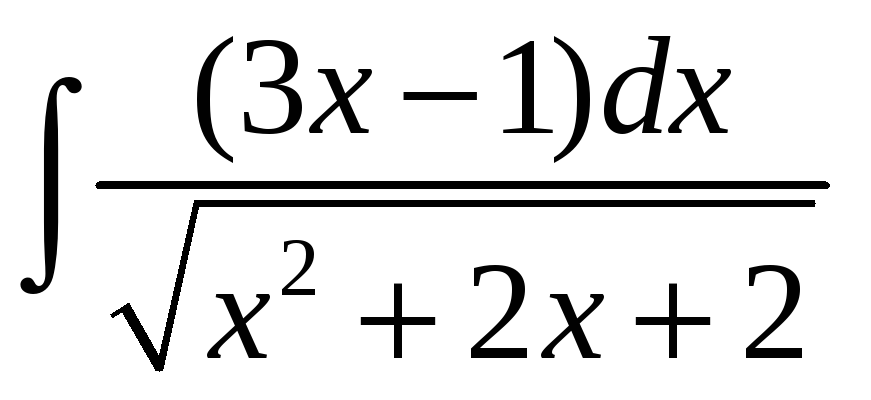 ;. в)
;. в)
![]() ;
;
г)
 ; д)
; д)
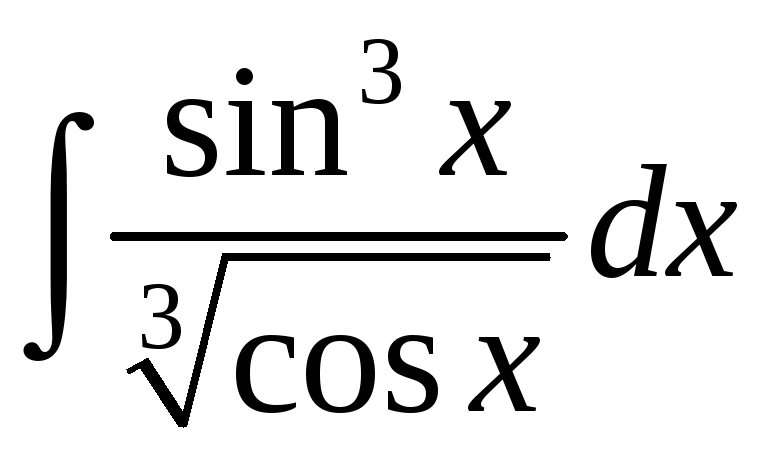 ;. е)
;. е)
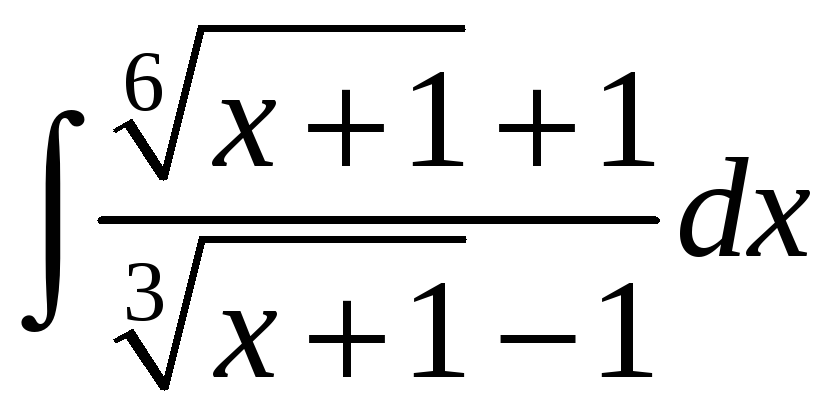 .
.
1.29
а)
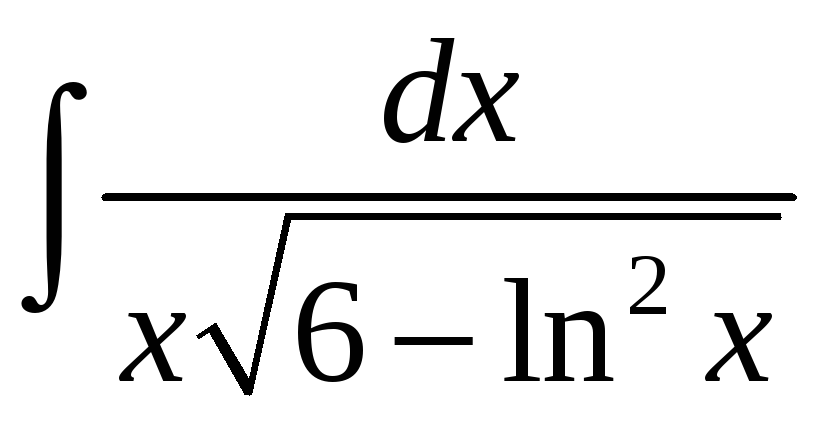 ; б)
; б)
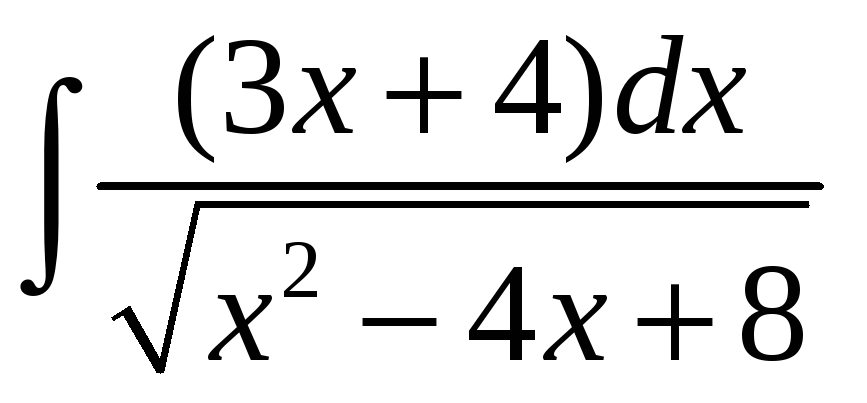 ;. в)
;. в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;. е)
;. е)
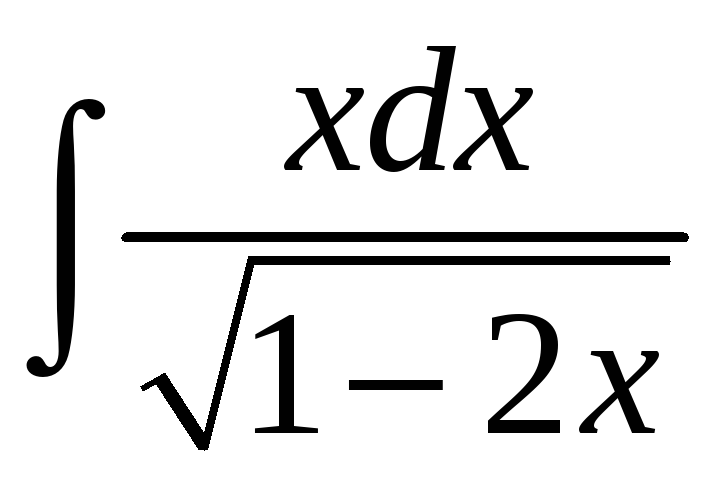 .
.
1.30
а)
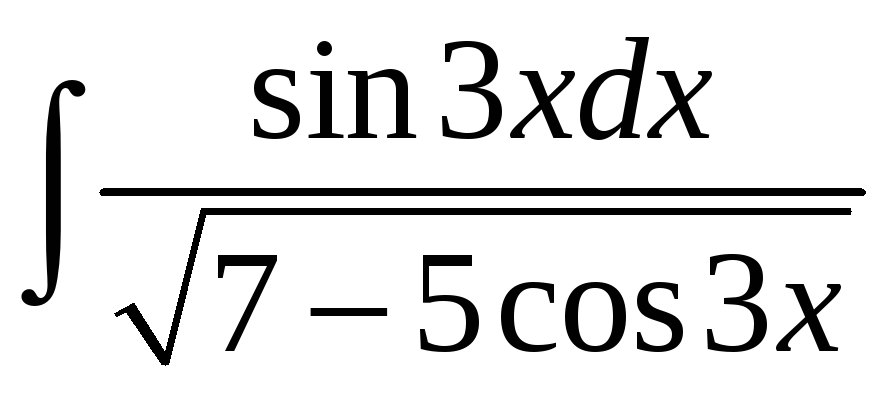 ; б)
; б)
![]() ;. в)
;. в)
![]() ;
;
г)
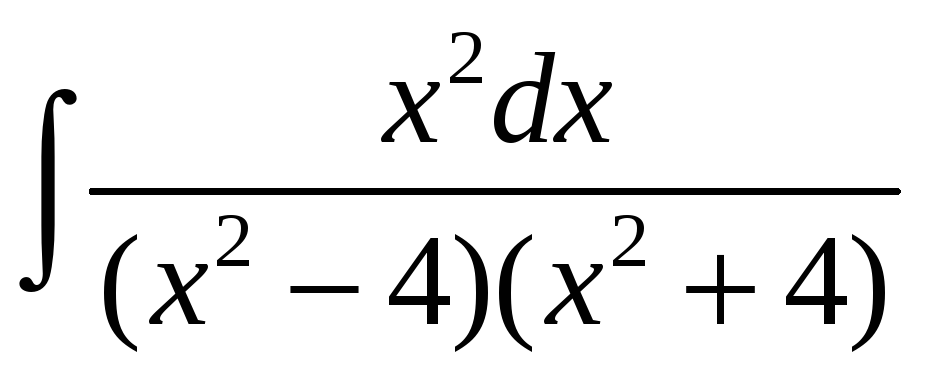 ; д)
; д)
![]() ;. е)
;. е)
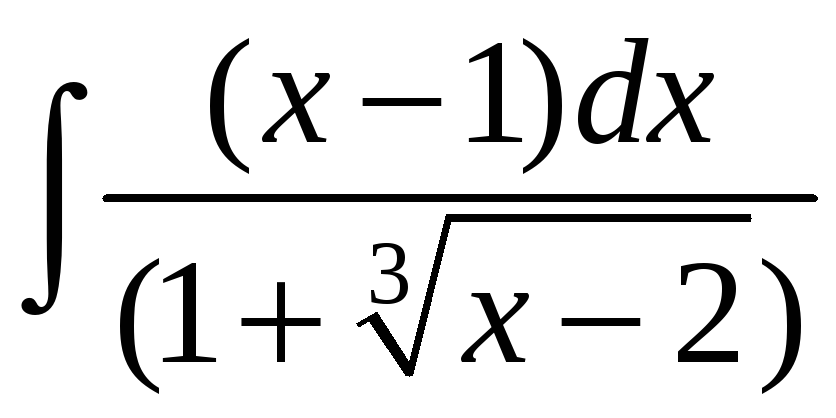 .
.
Тема 2. Определеный интеграл и его приложения
Интегральной
суммой
функции
![]() на отрезке
на отрезке
![]() называется сумма
называется сумма
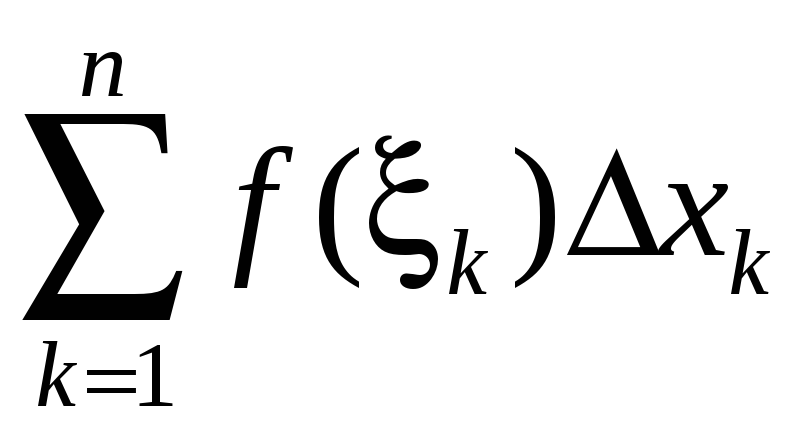 ,
где
,
где
![]() ,
причем
,
причем
![]() .
.
Если существует
предел интегральной суммы при
![]()
![]() ,
не зависящий от способа разбиения
отрезка
,
не зависящий от способа разбиения
отрезка
![]() на частичные отрезки
на частичные отрезки
![]() и выбора промежуточных точек
и выбора промежуточных точек
![]() ,
то функция
,
то функция
![]() называется интегрируемой
на этом
отрезке, а сам предел – определенным
интегралом от
функции
называется интегрируемой
на этом
отрезке, а сам предел – определенным
интегралом от
функции
![]() на отрезке
на отрезке
![]() и обозначается
и обозначается
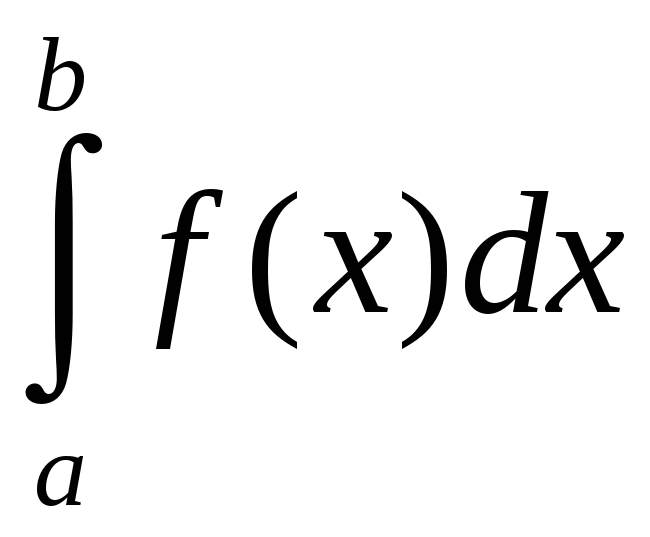 .
.
Таким образом,
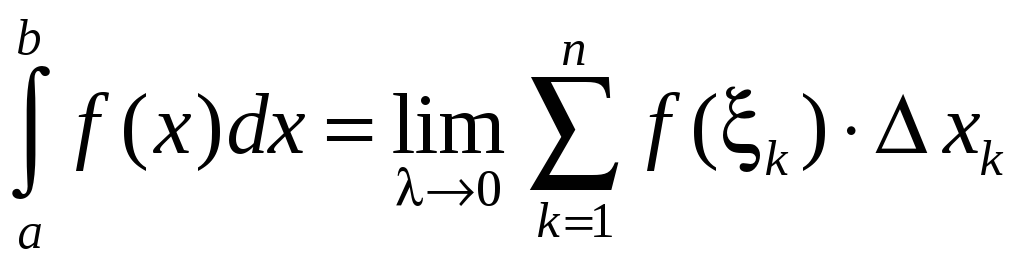 .
.
Если
![]() непрерывна на
непрерывна на
![]() ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
Пусть
![]() - одна из первообразных непрерывной на
- одна из первообразных непрерывной на
![]() функции
функции
![]() ,
тогда справедлива формула
Ньютона – Лейбница
,
тогда справедлива формула
Ньютона – Лейбница
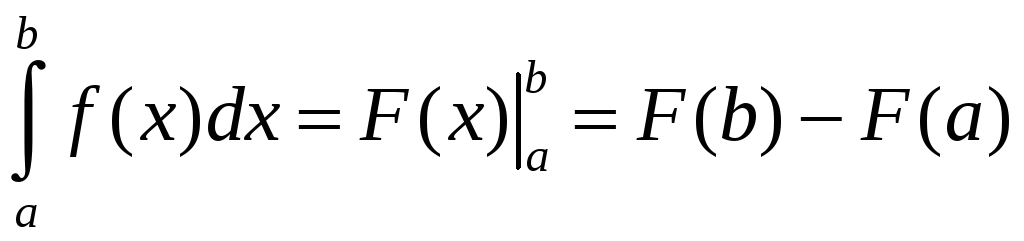 . (2.1)
. (2.1)
Если функции
![]() и
и
![]() непрерывны вместе со своими производными
на
непрерывны вместе со своими производными
на
![]() ,
то имеет место формула
интегрирования по частям
,
то имеет место формула
интегрирования по частям
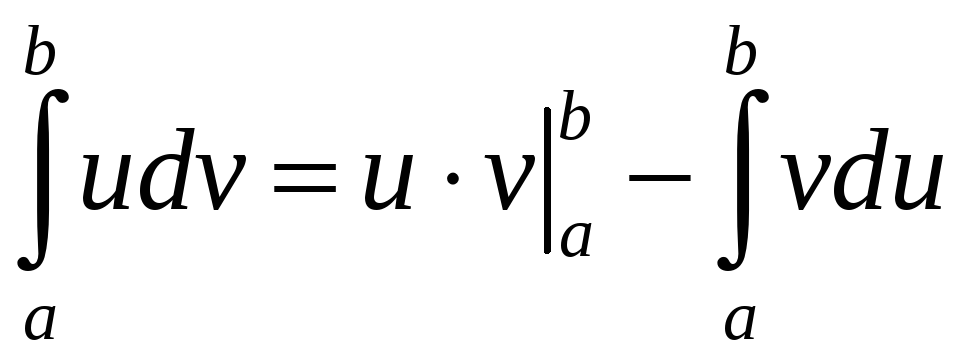 . (2.2)
. (2.2)
Если функция
![]() непрерывна на
непрерывна на
![]() ,
а функция
,
а функция
![]() непрерывно дифференцируема и строго
возрастает на
непрерывно дифференцируема и строго
возрастает на
![]() ,
то справедлива формула
,
то справедлива формула
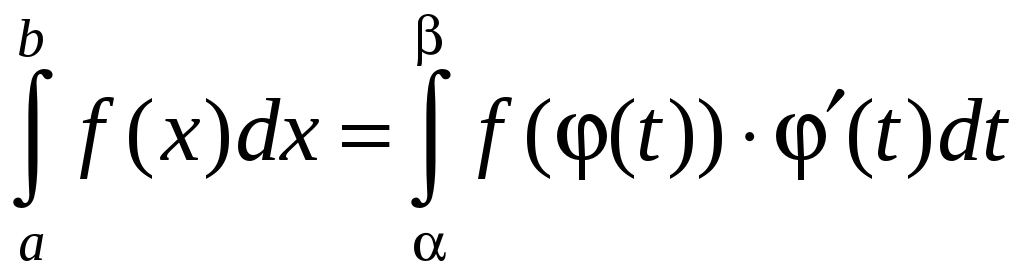 , (2.3)
, (2.3)
называемая формулой замены переменной в определенном интеграле.
Пример 2.1. Вычислить интегралы:
а)
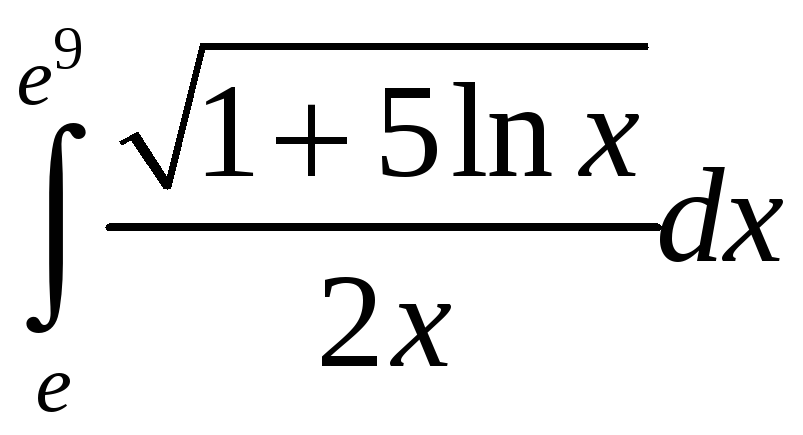 ; б)
; б)
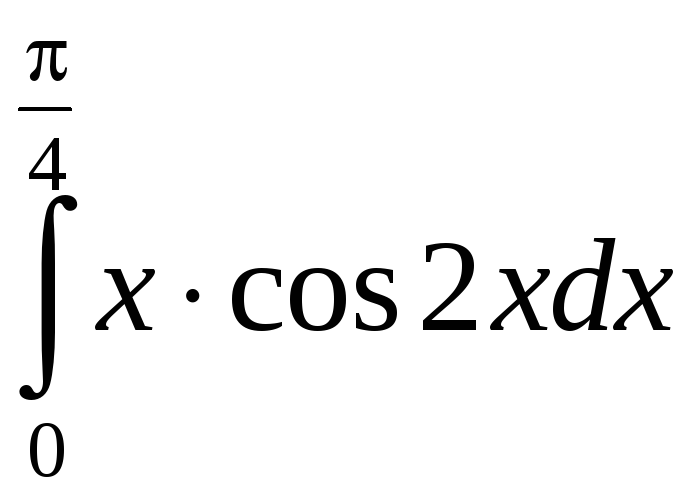 .
.
Решение.
а) Введем новую переменную интегрирования
![]() .
Тогда
.
Тогда
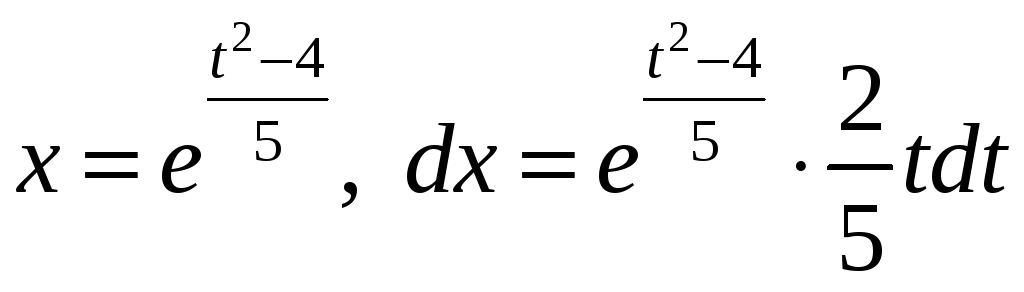 .
Найдем пределы интегрирования по
переменной
.
Найдем пределы интегрирования по
переменной
![]() .
Из формулы
.
Из формулы
![]() при
при
![]() ,
следует, что
,
следует, что
![]() ,
т.е.
,
т.е.
![]() ;
при
;
при
![]() ,
– следует, что
,
– следует, что
![]() ,
т.е.
,
т.е.
![]() .
Тогда по формуле (2.3) получаем
.
Тогда по формуле (2.3) получаем
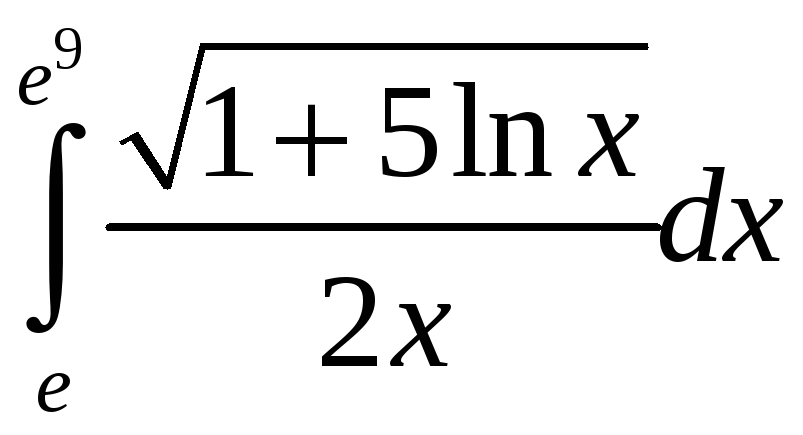 =
= .
.
б) Применим интегрирование по частям:
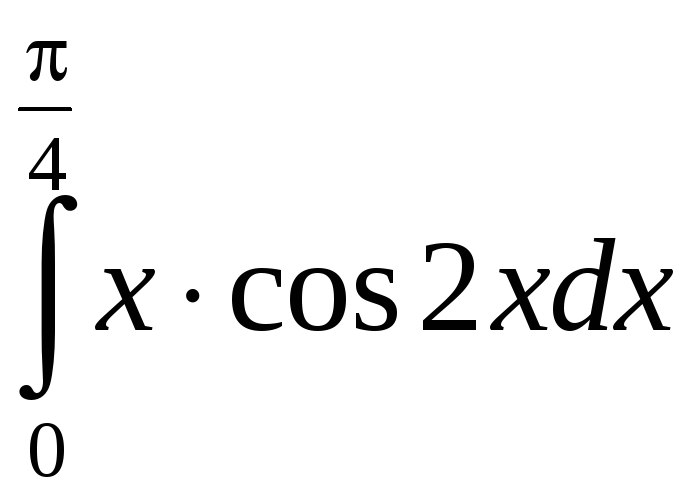 =
=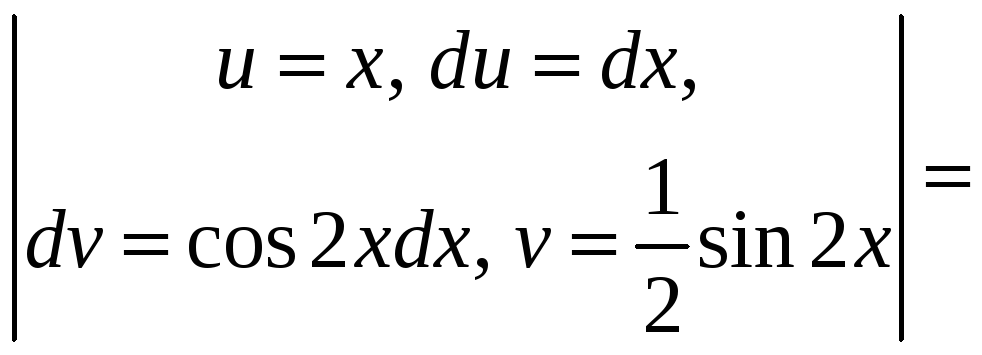
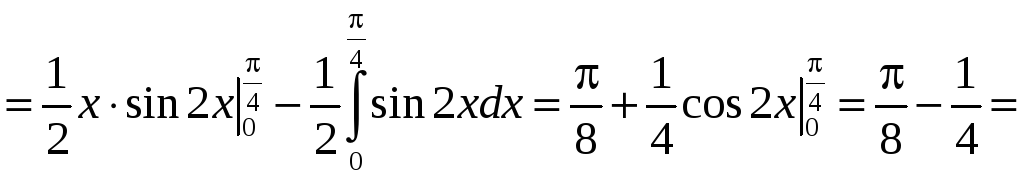
![]() .
.
Площадь
криволинейной трапеции,
ограниченной графиком функции
![]() ,
прямыми
,
прямыми
![]() и осью Ох
(рис.1), вычисляется по формуле
и осью Ох
(рис.1), вычисляется по формуле
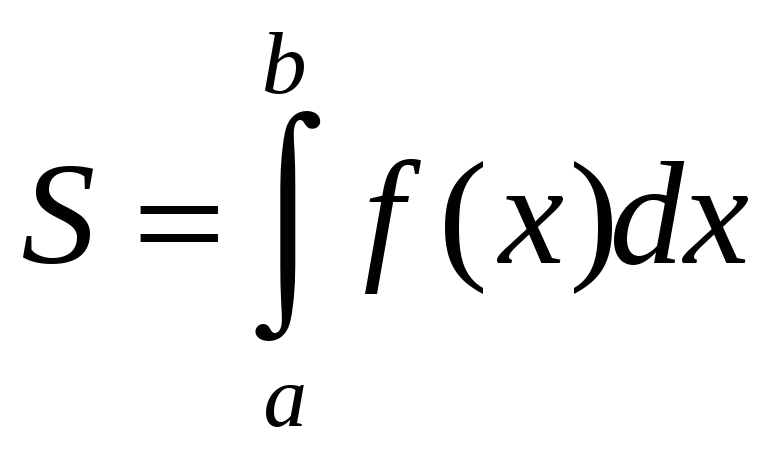 . (2.4)
. (2.4)
Если
![]() ,
то
,
то
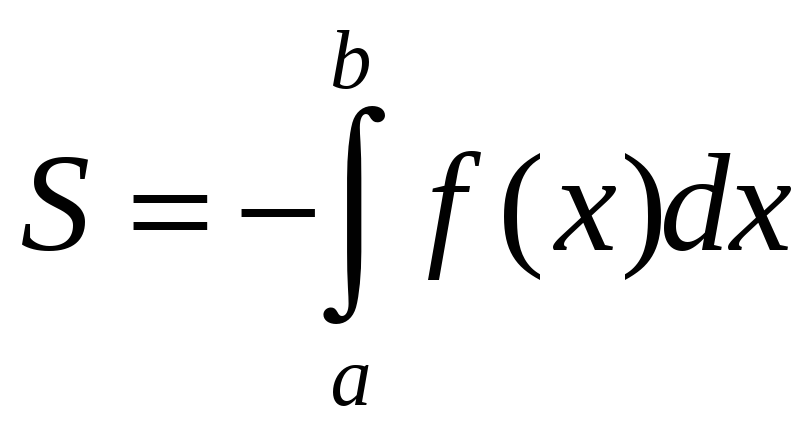 .
.
Площадь
плоской фигуры,
изображенной на рис.2 ( здесь
![]() ),
вычисляется по формуле
),
вычисляется по формуле
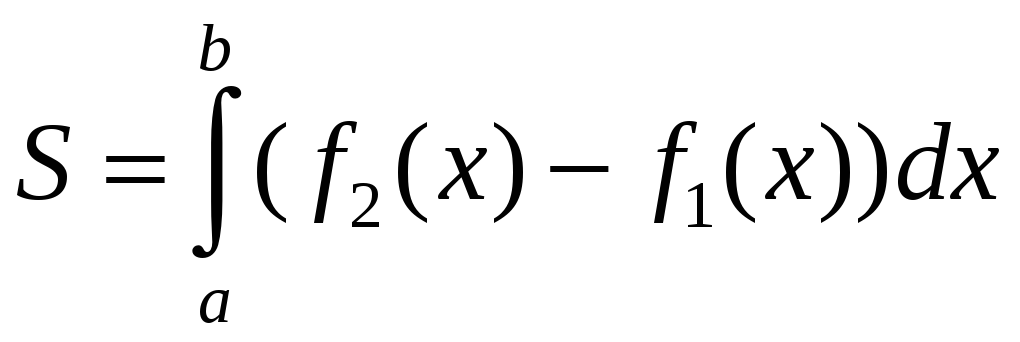
 (2.5)
(2.5)
Y
![]()
![]()
![]() X
X
Рис. 1.
 Y
Y
![]()
X
![]()
![]()
![]()
Рис. 2.
Пример 2.3. Вычислить
площадь фигуры, ограниченной линиями
![]() .
.
Решение. Даны
уравнения парабол и прямой. Параболы
построим, приведя их уравнения к виду
![]() и
и
![]() .
Проведя прямую
.
Проведя прямую
![]() ,
определим, площадь какой фигуры требуется
вычислить (рис.3). Ясно, что нижний предел
интегрирования в этой формуле равен
,
определим, площадь какой фигуры требуется
вычислить (рис.3). Ясно, что нижний предел
интегрирования в этой формуле равен
![]() .
Верхним пределом интегрирования будет
являться абсцисса одной из точек
пересечения парабол, которую найдем,
решая систему
.
Верхним пределом интегрирования будет
являться абсцисса одной из точек
пересечения парабол, которую найдем,
решая систему
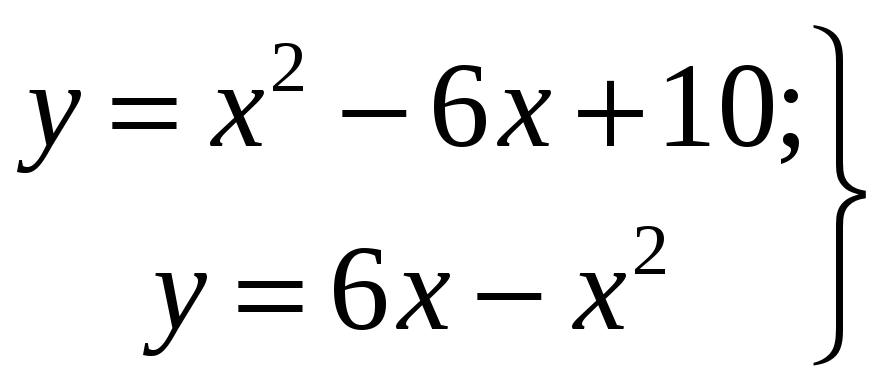
![]() .
.
Корень
![]() последнего уравнения и есть абсцисса
точки пересечения (второй корень
последнего уравнения и есть абсцисса
точки пересечения (второй корень
![]() ).
).
Y
0
-1 1 3 5 X
Рис. 3.
Имеем:
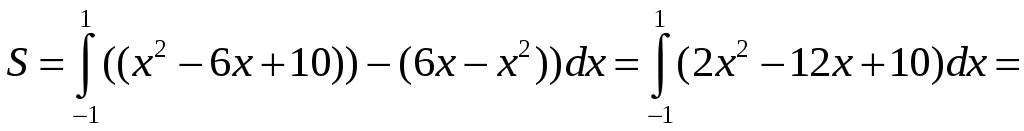
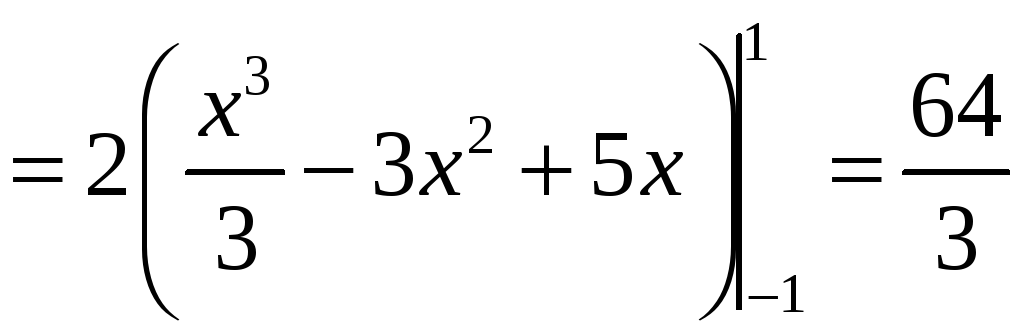 .
.
Объем тела,
образованного вращением вокруг оси Ох
криволинейной трапеции, которая
ограничена графиком функции
![]() ,
прямыми
,
прямыми
![]() и осью Ох
вычисляется по формуле
и осью Ох
вычисляется по формуле
 , (2.6)
, (2.6)
Если фигура,
ограниченная графиком двух функций
![]() и
и
![]()
![]() и прямыми
и прямыми
![]() ,
вращается вокруг оси Ох,
то объем тела вращения
,
вращается вокруг оси Ох,
то объем тела вращения
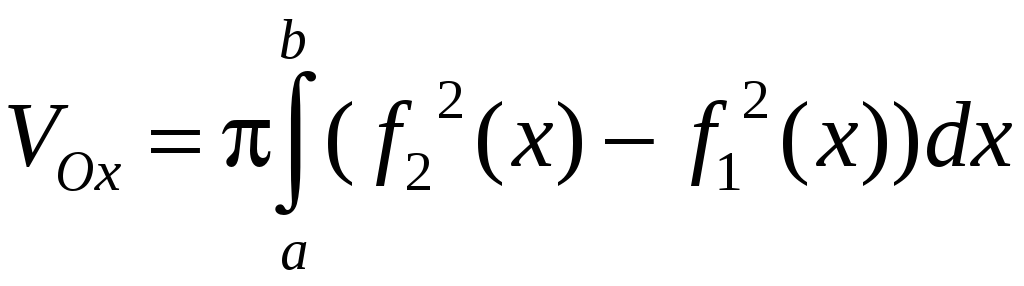 (2.7)
(2.7)
Пример 2.4. Вычислить
объем тела, образованного вращением
вокруг оси Ох
фигуры, ограниченной линиями
![]() .
.
Решение. Построив
окружность
![]() и прямую
и прямую
![]() ,
получим круговой сегмент (рис. 4). При
вращении его вокруг оси Ох
образуется тело, объем
,
получим круговой сегмент (рис. 4). При
вращении его вокруг оси Ох
образуется тело, объем
![]() которого вычисляется по формуле (2.7),
так как этот сегмент ограничен графиком
двух функций
которого вычисляется по формуле (2.7),
так как этот сегмент ограничен графиком
двух функций
![]() и
и
![]() ,
причем
,
причем
![]() .
Таким образом,
.
Таким образом,
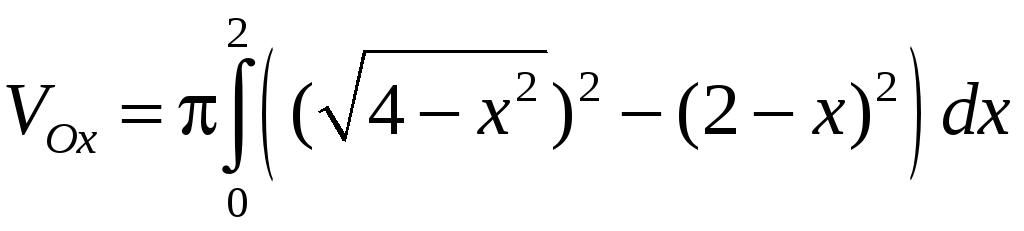 =
=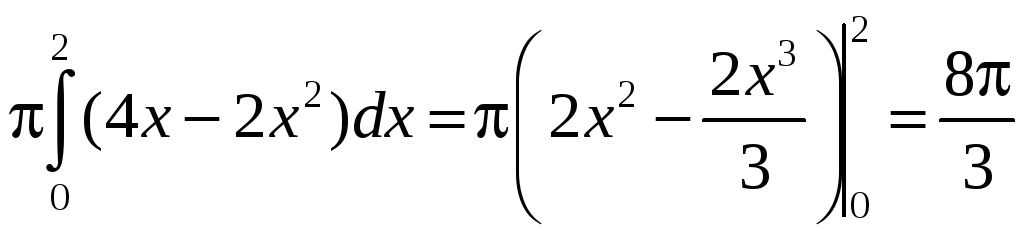 .
.
Y
2
X
0 2
Рис. 4.
Если плоская кривая
задана уравнением
![]() ,
то длина ее дуги от точки А
с абсциссой a
до точки В
c
абсциссой
,
то длина ее дуги от точки А
с абсциссой a
до точки В
c
абсциссой
![]() вычисляется по формуле
вычисляется по формуле
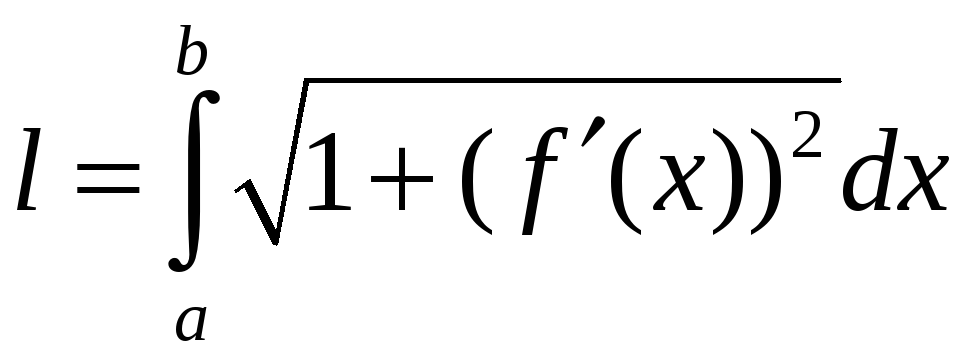 (2.8)
(2.8)
Если кривая задана параметрически:
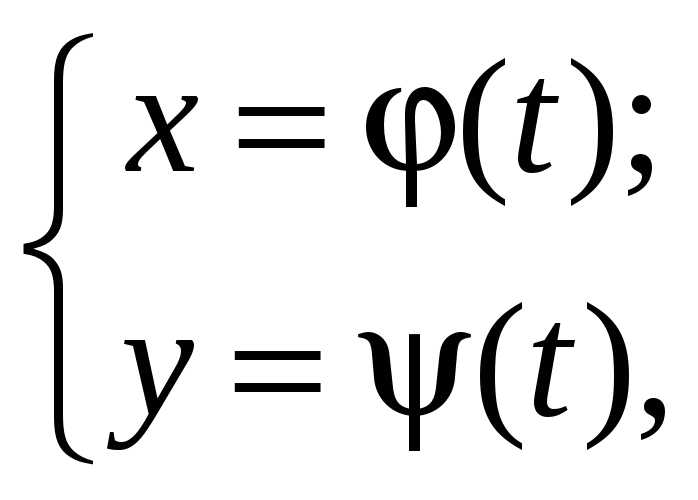 ,
где
,
где
![]() (
(
![]() значения параметра
значения параметра
![]() ,
соответствующие концам рассматриваемой
дуги), то длина дуги определяется формулой
,
соответствующие концам рассматриваемой
дуги), то длина дуги определяется формулой
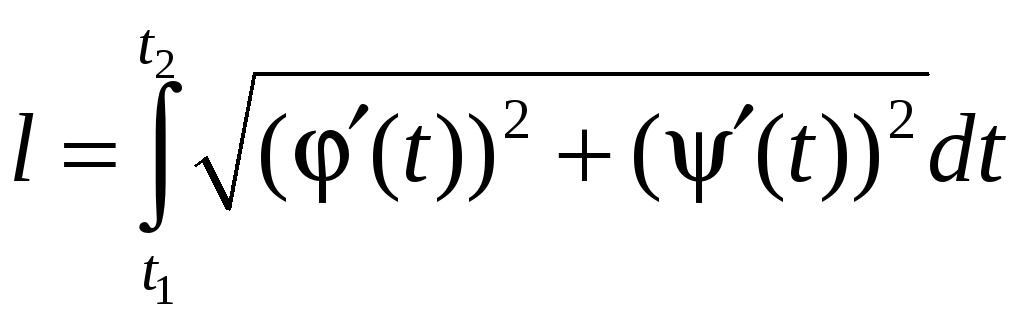 (2.9)
(2.9)
Пример 2.5. Вычислить длину дуги кривой, заданной уравнениями:
а)
![]() от начала координат до точки
от начала координат до точки
![]() ;
;
б)
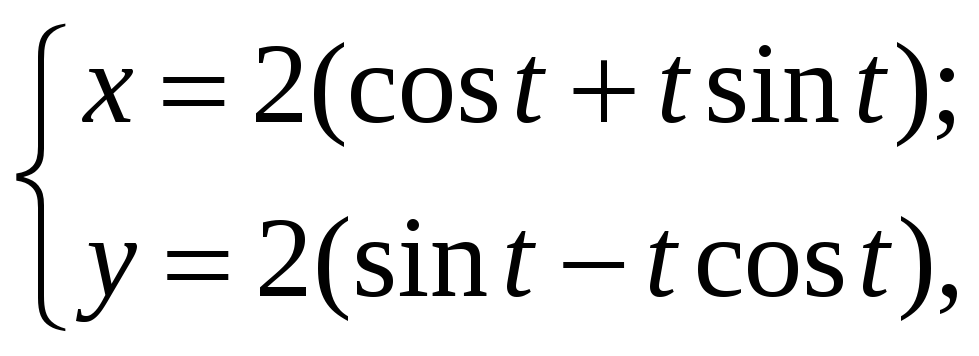 при
при
![]() .
.
Решение. а)
Находим
 .
.
В соответствии с
формулой (2.8) (полагая в ней
![]() )
имеем:
)
имеем:
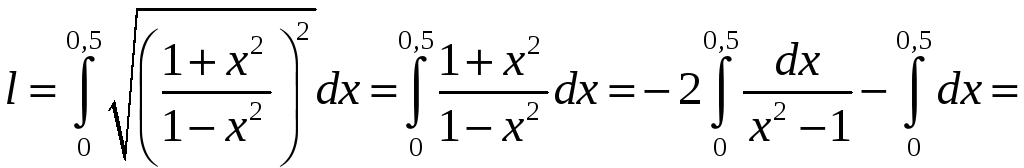
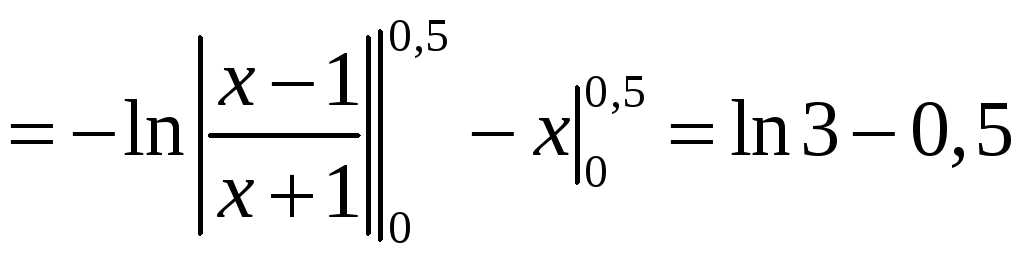 .
.
б) Вычисляем
![]() ,
,
![]() ,
,
![]() .
.
Согласно формуле (2.9) имеем:
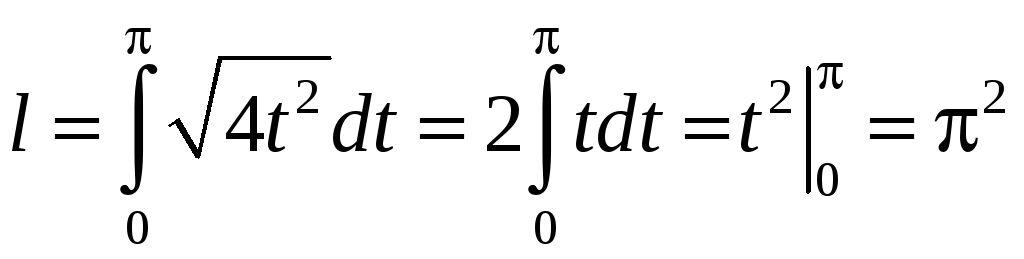 .
.
