20.. Закон сохранения энергии в механике. Примеры.

закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.

Рассмотрим систему материальных точек массами , движущихся со скоростями . Пусть — равнодействующие внутренних консер­вативных сил, действующих на каждую из этих точек, а — равнодейст­вующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим

Двигаясь под действием сил, точки системы за интервал времени совершают перемещения,

соответственно равные. Умножим каждое из уравнений скалярно на соответствующее перемещение и сложим, учитывая, что. Получим:

Первый член левой части равенства равен приращению кинетической энергии системы (). Второй член равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергии системы ().Правая часть равенства задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем

При переходе системы из состояния 1 в какое-либо состояние 2т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативным силами. Если внешние неконсервативные силы отсутствуют, то

_, ,

21-22. Моменты импульса и силы относительно точки и неподвижной оси. Уравнение моментов для системы материальных точек.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

,

где - радиус вектор, проведенный из точки О в точку А; - импульс материальной точки; — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к . Модуль вектора момента импульса равен:

,

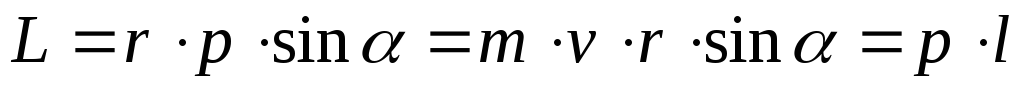где - угол между векторами к , - плечо вектора относительно точки О.

Моментом импульса относительно неподвижной оси называется скалярная величина , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса , не зависит от положения точки О на оси . При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдель­ная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, т. е. радиус является плечом вектора . Поэтому можем записать, что момент импульса отдель­ной частицы равен: и направлен по оси в сторону, определяемую правилом правого винта.

23Теорема Штейнера-Гюгенса-если ось вращения твердого тела не проходит через центр масс то момент инерции ТВ.тела относительно данной оси вычисл как сумма 2-ух слогаемых 1-момент инерции относ оси прох через центр масс данного тела и и H данной оси вращ +массу ТВ тела на квадрат расстояния между осями I=Ic+md2

24.Уравнение моментов=моменту инерции отн неподв оси на угловое ускорение и это произв=алгебр сумме моментов вращ.всех сил приложенных к данному телу I×E=∑Mi

25Закон сохранения момента импульса пример Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

,

где - радиус вектор, проведенный из точки О в точку А; - импульс материальной точки; — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к . Модуль вектора момента импульса равен:где - угол между векторами к , - плечо вектора относительно точки О.закон-момент импульса физической системы ,на которую не действуют внеш силы,сохраняется

26Гармонические колебания .Уравн колебаний осцилятораи его решениеГармонические колебания величины s описываются уравнением типа

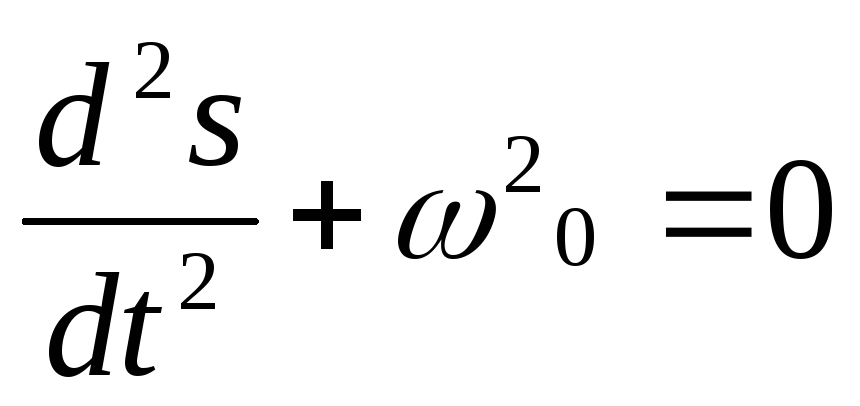Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида:

Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур

1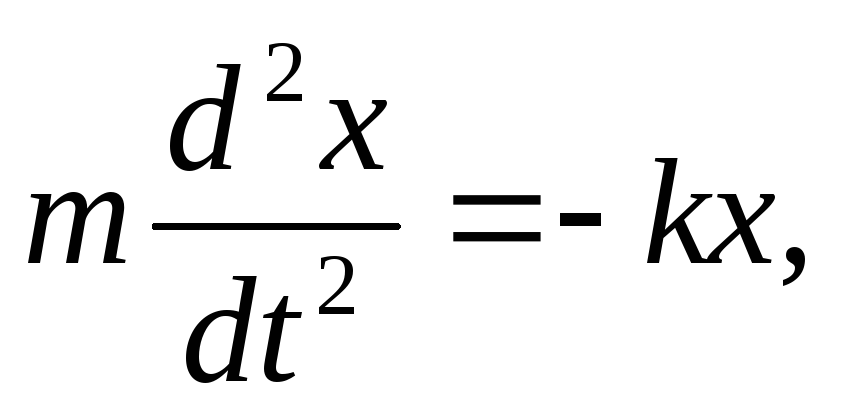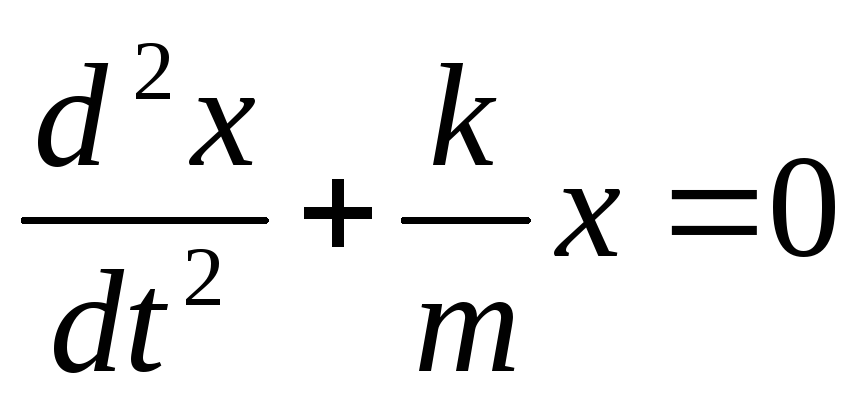. Пружинный маятник — это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F= -kx, где k — жесткость пружины.

(3.2)

Из выражений (3.1) и (3.2) следует, что пружинный маятник совершает гармонические колебания по закону x=Acos(ω₀t+φ) с циклической частотой

2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела

27.Характеристики гармон колеб их определ и единицы измер уравнение гарм колебаний x=A×cos(wt+0) x-величина смещения от положения равновесия,А-амплитуда.w-циклическая частота связанная с частотой v соотношением w=2∏v, -фаза колебания,0-начальная фаза колебания. частота в СИ=1Гц-число колебаний в единицу времени,циклическая с-1 амплитуда-модуль максимального отклонения физ величины от ее среднего значения

28.Матем и физич маятник уравнения их колебаний1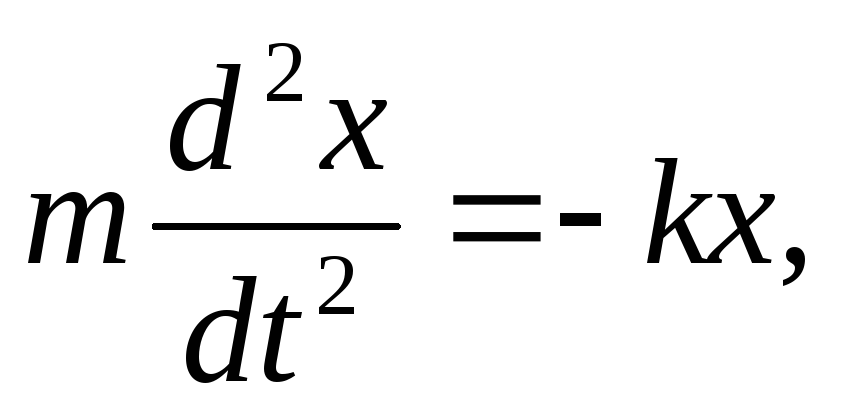. Пружинный маятник — это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F= -kx, где k — жесткость пружины.

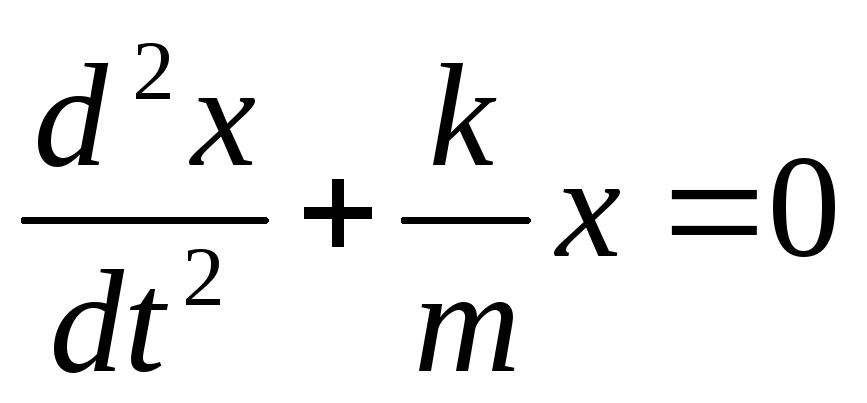
T=2п

(3.2)

Из выражений (3.1) и (3.2) следует, что пружинный маятник совершает гармонические колебания по закону x=Acos(ω₀t+φ) с циклической частотой

2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела

30Сложение гарм кол 1 частоты. Биение x1=A1cos(w0t+1) x2=A2cos(w0t+2) x1+x2= ,биение-это когда частоты не совпадают

31сложение взаимноперпен колебаний.Фигуры Лисажу.x=acoswt, y=bcos(wt+α)/ тогда ,

если частоты перпен колебаний не одинаковы то траектория движения имеет вид довольно сложных кривых-фигуры Лиссажу

33Вынужденые колебания .Резонанс в механике вын-колебания,возникающие под действием внешней периодически изменяющейся силы. Если частота внешней силы совпадает с частотой свободных колебаний системы, амплитуда колебания резко возрастает это явление называется резонансом. Чем меньше трение тем больше амплитуда резонансных колебаний и тем острее пик на резонансной кривой

34.Статический и термодинамический метод исследования статический-интересуется недвижением отдельных молекул, а лишь средними величинами, которые характеризуют движение огромной совокупности частиц. термод-изучает макроскопические свойства тел и явлений природы не интересуясь их микроскопической картиной. не вводя в рассмотрение малекулы и атомы термодин позволяет делать целый ряд выводов относително их протекания

35Макроскопические параметры и их определение ед изм-объем,температура,давление, вн энергия

36Уравнение состояния идеального газа.малярная масса число Авагадро число Авогадро –число малекул в 1 моле вещества=6,02. 10(23) моль-1 молярная масса-маса 1 моля вещества М=NAумножm0 –масса малекулы данного вещ P=1|3nm0v2

37Тепловое движение.МКТ. Внутреняя энергия В основе МКТ лежат ти положения:

-Все вещества состоят из мельчайших частиц – молекул .

-Молекулы находятся в непрерывном хаотическом движении.

- Между молекулами действуют силы притяжения и силы отталкивания. Если поверхностные силы значительно больше веса жидкости или жидкость находится в невесомости, то можно считать, что жидкость сжата только поверхностными силами, и весом жидкости можно пренебречь. Условие равновесия выделенной жидкости макрочастицы:

_{внутренняя энергия-энергия теплового движения микрочастиц системы и энергия взаимодействия этих частиц}