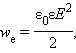Билет 8 (а)(б)Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

В системе СИ единица электроемкости называется фарад (Ф):

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 1.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 1.6.2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля

Рисунок 1.6.1. Поле плоского конденсатора

Рисунок 1.6.2. Идеализированное представление поля плоского конденсатора. Такое поле не обладает свойством потенциальности

Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением

Согласно принципу суперпозиции, напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин:

Внутри конденсатора вектора и параллельны; поэтому модуль напряженности суммарного поля равен

Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:

Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы. Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R₁ и R₂. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R₁ и R₂ и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:

(сферический конденсатор), (цилиндрический конденсатор).

Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.6.3) напряжения на конденсаторах одинаковы: U₁ = U₂ = U, а заряды равны q₁ = С₁U и q₂ = C₂U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q₁ + q₂ при напряжении между обкладками равном U. Отсюда следует

Таким образом, при параллельном соединении электроемкости складываются.

Рисунок 1.6.3. Параллельное соединение конденсаторов. C = C1 + C2

Рисунок 1.6.4. Последовательное соединение конденсаторов.

При последовательном соединении (рис. 1.6.4) одинаковыми оказываются заряды обоих конденсаторов:

q₁ = q₂ = q, а напряжения на них равны и Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U₁ + U₂. Следовательно,

(В) Опыт показывает, что заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу

Энергия W_е конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

Рисунок 1.7.1. Процесс зарядки конденсатора

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

Электрическую энергию W_е следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для W_е аналогичны формулам для потенциальной энергии E_р деформированной пружины (см. ч. I, § 2.4)

где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.

Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость Поэтому

где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности w_е по всему объему, в котором создано электрическое поле.

БИЛЕТ 9

Взаимодействие токов. Магнитное поле. Графическое изображение магнитных полей проводников с токами различной формы. Правило буравчика.

Движущиеся заряды образуют электрический ток. Следовательно, магнитное поле – это поле, создаваемое электрическим током. Оно осуществляет взаимодействие электрических токов.

Взаимодействие между проводниками с током, т.е. взаимодействия между движущимися электрическими зарядами, называют магнитными. Силы, с которыми проводники с током действуют друг на друга, называются магнитными силами.

Магнитное поле – особый вид материи, который обладает определенными свойствами:

1. оно существует независимо от нас и наших знаний о нём

2. оно порождается движущими заряженными частицами

3. оно воздействует на проводник с током и на движущиеся заряженные частицы.

У постоянных магнитов магнитное поле возникает благодаря движущихся электронов вокруг ядер.

Магнитное поле необходимо измерять, поэтому вводят величину – магнитная индукция.

1. направление вектора магнитной индукции.

• Направление вектора магнитной индукции поля созданного векторами с током. Правило буравчика – если вращаемое движение ручки буравчика направленно по направлению с движением тока в витке, то поступательное движение кончика буравчика, совпадает с направлением вектора магнитной индукции.

• Направление вектора магнитной индукции прямолинейного проводника с током. Правило буравчика – если поступательное движение кончика буравчика совпадает с направлением тока в проводнике, то вращательное движение ручки буравчика совпадает с направлением вектора магнитной индукции. Силовые линии магнитного поля – это непрерывные линии, касательные к которым направлены так же, как и вектор В в данной точке поля ( в каждой точке совпадает с вектором магнитной индукции). Для постоянного магнита силовые линии проходят внутри него, выходя из северного полюса, а входя в южный. Отличительная особенность магнитного поля от электрического в том, что оно не имеет отдельных зарядов.

БИЛЕТ 10

Действие магнитного поля на движущийся заряд. Сила Лоренца. Правило левой руки. Движение заряженной частицы в магнитном поле.

Магнитное поле действует не только на проводник с током, но и на отдельно движущуюся заряженную частицу. Эту силу называют Силой Лоренца (Fл). Она зависит от модулей скорости частицы и индукции магнитного поля.

, где В-вектор магнитной индукции, q-заряд, V-скорость, α-угол между В и направлением движения положительно заряженной частицы.

Правило левой руки:

Если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90⁰ большой палец покажет направление действующей на заряд силы Лоренца Fл.

Сила Лоренца перпендикулярна направлению движущей частицы, поэтому сила Лоренца не производит работы, а значит не изменяет кинетической энергии. Значит скорость не изменяется и сила Лоренца действует только на изменение направления. Определить по какой траектории будет двигаться частица, если она влетает в магнитное поле перпендикулярно вектору магнитной индукции. Сила Лоренца будет заставлять частицу заворачивать, не изменяя скорости и придавать ей центростремительное ускорение.

БИЛЕТ 11

Действие магнитного поля на проводник с током. Сила Ампера. Правило левой руки. Магнитная индукция.

Величина вектора магнитной индукции.

Магнитное поле действует на проводник с током. Силу с которой поле действует называется – Сила Ампера.

Fa=BIl(дельта)sinα, где B – вектор магнитной индукции, I – сила тока в проводнике, l(дельта) – участок проводника на который действует магнитное поле, α – угол между проводником и вектором магнитной индукции.

Сила ампера равна произведению вектора магнитной индукции на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника.

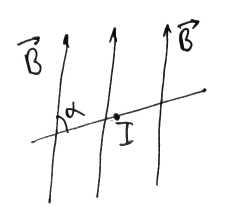
Сила Ампера мах, когда α=90⁰

Магнитное поле необходимо измерять, поэтому вводят величину магнитная индукция. АГНИТНАЯ ИНДУКЦИЯ (обозначается В), среднее результирующее магнитное поле в веществе.

Индукция магнитного поля в 1 Тл, это индукция, которая действует на проводник длинной 1 м с силой тока 1А с силой 1Н.

Модулем вектора магнитной индукции называется отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка: B=Fm/Il(дельта).

Правило левой ладони для определения направления силы ампера.

Если перпендикулярно составленный вектор магнитной индукции входит в ладонь, а четыре сомкнутых пальца совпадают с направлением силы тока в проводнике, то отогнутый на 90⁰ большой палец показывает направление силы ампера.

Принцип суперпозиции для магнитных полей: если в некоторых точках пространства действует несколько магнитных полей, то индукция результирующего поля есть векторная сумма индукции отдельных полей.

Несколько формул применяемых для нахождения вектора магнитной индукции.

1. B – магнитная индукция прямолинейного, бесконечного проводника с током, где I – сила тока, r – расстояние до точки в которой измеряют индукцию. µ₀ – магнитная постоянна. µ₀=4П*10^-7 Тл*м/А

2. магнитная индукция поля в центре кругового витка с током. R – радиус витка.

3. Магнитная индукция поля внутри цилиндра катушки с током (соленоид) n – число витков, а L – длина катушки.