
- •Тема 10. Хеджирование ценовых рисков с помощью фьючерсных контрактов
- •10.1. Общая характеристика фьючерсного контракта
- •10.2. Организация фьючерсной торговли
- •Взаиморасчеты по фьючерсному контракту, производимые расчетной палатой
- •10.3. Фьючерсная цена. Базис.
- •10.4. Цена доставки
- •Тема 11. Хеджирование риска с помощью опционных контрактов
- •11.1. Общая характеристика опционного контракта
- •11.2. Категории опционов. Премия
- •11.3. Простейшие опционные стратегии
- •11.4. Определение стоимости опциона
- •11.4.1. Простейшая биноминальная модель
- •11.4.3. Модель Блэка-Шоулза
- •11.4.4.Оценка стоимости американских опционов в условиях биноминальной модели
- •Тема 12. Управление портфелем облигаций
- •12.1. Сущность облигаций
- •12.2. Временная структура процентных ставок. Форвардная процентная ставка
- •12.3. Процентный риск облигации. Дюрация и выпуклость
- •12.4. Доходность портфеля облигаций
- •12.5. Дюрация и выпуклость портфеля облигаций
- •12.6. Стратегии управления портфелем облигаций
- •13. Управление кредитными рисками
- •13.1.Общая характеристика кредитного риска
- •13.2. Кредитное событие
- •13.3.Анализ кредитоспособности заемщика
12.5. Дюрация и выпуклость портфеля облигаций
Предположим, что
на рынке присутствуют облигации l
видов , стоимость которых в данный
(нулевой) момент равны соответственно
![]() .
Будем считать, что данные облигации
можно покупать в любом количестве.
.
Будем считать, что данные облигации
можно покупать в любом количестве.
Инвестор, затратив
на покупку сумму
![]() на покупку облигаций j-го
вида (j
= 1,2,3, …, l),
сформирует портфель облигаций
на покупку облигаций j-го
вида (j
= 1,2,3, …, l),
сформирует портфель облигаций
![]() стоимостью
стоимостью
![]() .
.
Портфель облигаций
![]() эквивалентен облигации стоимостью
эквивалентен облигации стоимостью
![]() ,
по которой в моменты
,
по которой в моменты
![]() должны выплачиваться соответствующие
денежные суммы
должны выплачиваться соответствующие
денежные суммы
![]()
![]()
![]()
где
![]() - платеж по j-той
облигации в момент времени
- платеж по j-той
облигации в момент времени
![]() (i
= 1,2, …, n).
(i
= 1,2, …, n).
Дюрацией
![]() и соответственно выпуклостью
и соответственно выпуклостью
![]() портфеля облигаций П при начислении
процентов m
раз в год называется дюрация и выпуклость
облигации, эквивалентной этому портфелю
облигаций.
портфеля облигаций П при начислении
процентов m
раз в год называется дюрация и выпуклость
облигации, эквивалентной этому портфелю
облигаций.
Если r – внутренняя доходность портфеля облигаций П при начислении процентов m раз в год, то
 [78]
[78]
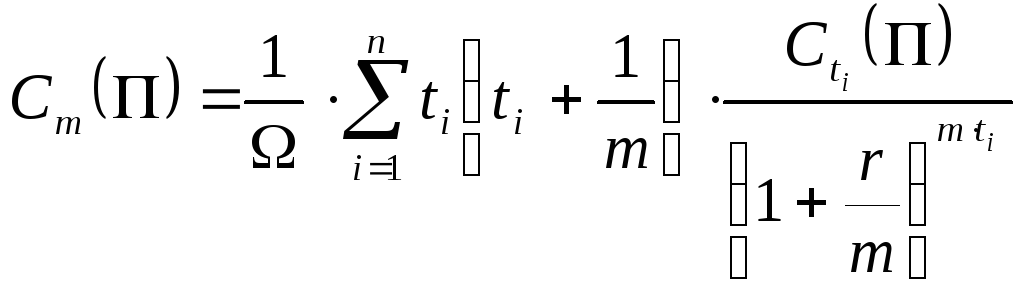 [79]
[79]
Модифицированная дюрация и выпуклость определяются по формуле:
 ,
,
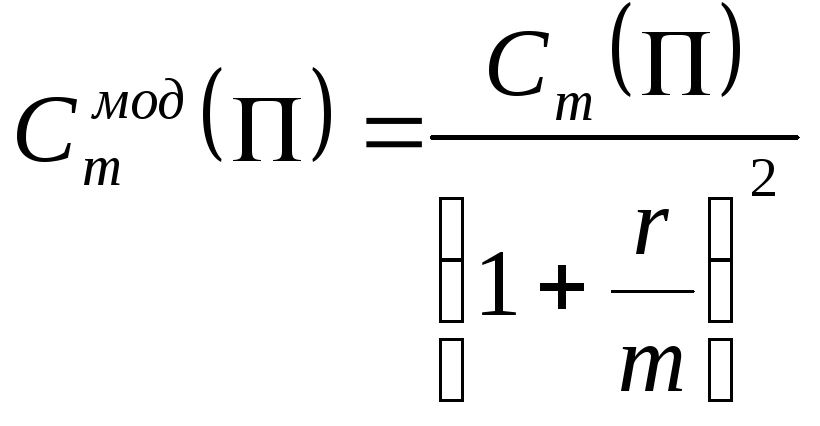 [80]
[80]
Относительное изменение стоимости портфеля облигаций при изменении процентных ставок определяется по формуле:
![]() [81]
[81]
где
![]() - изменение внутренней доходности
портфеля облигаций П;
- изменение внутренней доходности
портфеля облигаций П;
![]() - относительно
изменение стоимости портфеля облигаций
П;
- относительно
изменение стоимости портфеля облигаций
П;
Пример. Временная структура процентных ставок при начислении процентов дважды в год приведена ниже.
|
Срок, годы |
0,5 |
1,0 |
1,5 |
2,0 |
|
Безрисковая процентная ставка,% |
6 |
6,5 |
6 |
8 |
Рассмотрим портфель П=П(2000,1000,500) из облигаций, основные характеристики которых приведены в табл. 9.
Таблица 9
Исходные данные
|
Облигация |
Платежи по срокам, долл. |
|||
|
0,5 |
1 |
1,5 |
2 |
|
|
А |
6 |
6 |
6 |
106 |
|
В |
10 |
|
110 |
|
|
С |
8 |
100 |
|
|
Необходимо определить модифицированную дюрацию и выпуклость портфеля облигаций П.
Решение. Сначала необходимо определить рыночную стоимость облигаций, входящих в портфель.
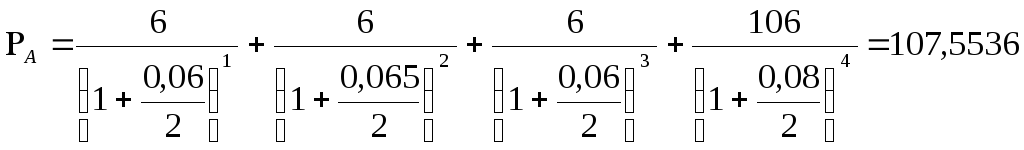
Аналогично получили курсы облигаций В и С, которые составили 110,3743 и 101,5707 долл. соответственно.
Теперь нужно определить поток денежных средств, генерируемый портфелем облигаций П.
![]()
![]()
![]()
![]()
Для нахождения дюрации и выпуклости портфеля облигаций необходимо определить внутреннюю доходность портфеля П. Для этого нужно решить следующее уравнение:
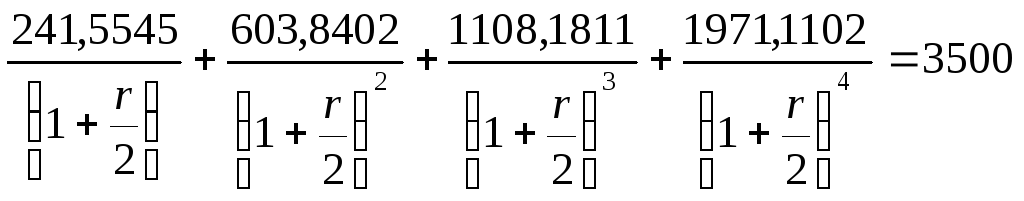
Решив данное уравнение, получаем, внутренняя доходность портфеля облигаций равна 7,264%. Теперь можно найти дюрацию и выпуклость портфеля облигаций П используя формулы [78] и [79].

![]()
Тогда


Кроме того, существует понятие средневзвешенной дюрации и выпуклости портфеля облигаций П.
Средневзвешенной
дюрацией
(средневзвешенной выпуклостью) портфеля
облигаций
![]() называется взвешенная по стоимости
сумма модифицированных дюраций
(модифицированных выпуклостей) облигаций
этого портфеля, т.е.
называется взвешенная по стоимости
сумма модифицированных дюраций
(модифицированных выпуклостей) облигаций
этого портфеля, т.е.
![]() [82]
[82]
![]() [83]
[83]
