
- •1. Теорема Фробениуса-Перрона. Определение числа и вектора Фробениуса неотрицательной матрицы.
- •3. Докажите следующее утверждение. Пусть s и s – минимальная и максимальная суммы элементов столбцов матрицы а. Тогда число Фробениуса λА матрицы а удовлетворяет неравенству s
- •5. Сформулируйте и докажите первый критерий продуктивности
- •6. Докажите, что если неотрицательная квадратная матрица продуктивна, то ее число Фробениуса меньше 1
- •7. Сформулируйте определение запаса продуктивности неотрицательной матрицы. Выведите формулу для вычисления запаса продуктивности через число Фробениуса.
- •9. Приведите примеры задач лп на минимум (задача о диете) и на максимум (задача об использовании ресурсов)
- •10. Приведите общую постановку злп. Дайте определения следующим терминам: целевая ф-ия, допустимое мн-во задачи, оптимальное решение, оптимальное мн-во.
- •26.Приведите пример двух взаимно двойственных задач лп. Сформулируйте правило построения двойственной задачи.
- •27. Сформулируйте и докажите основное неравенство для взаимно двойственных задач лп. Сформулируйте достаточный признак оптимальности.
- •28. Сформулируйте первую и вторую теоремы двойственности. Докажите вторую теорему двойственности (теорему равновесия)
- •29. Приведите пример постановки транспортной задачи. Что такое оптимальный план перевозок? Что такое транспортная задача с правильным балансом? Сформулируйте критерий разрешимости транспортной задачи.
- •30. Опишите методы построения начального опорного плана транспортной задачи (метод северо-западного угла, метод минимального тарифа.
- •38. Опишите модель Самуэльсона-Хикса. Какие экономические предположения лежат в ее основе? Запишите уравнение Хикса. В каком случае решением уравнения Хикса является стационарная последовательность?
- •39. Опишите паутинную модель рынка. Какие экономические предположения лежат в ее основе? Найдите равновесное состояние паутинной модели рынка.
1. Теорема Фробениуса-Перрона. Определение числа и вектора Фробениуса неотрицательной матрицы.
Для любой неотрицательной матрицы А=>0
существует собственное значение λА=>0
(называемое числом Фробениуса) такое,
что λА=>|λ| для любого собственного
значения λ матрицы А. Кроме того,
существует неотрицательный собственный
вектор
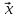 А=>0,
соответствующий собственному значению
λА и называемый вектором Фробениуса.
Причём, если А>0, то λА>0 и
А=>0,
соответствующий собственному значению
λА и называемый вектором Фробениуса.
Причём, если А>0, то λА>0 и
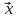 А>0
А>0
2. Докажите следующее утверждение: если
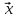 >0
– собственный вектор неотрицательной
матрицы, то он является ее вектором
Фробениуса.
>0
– собственный вектор неотрицательной
матрицы, то он является ее вектором
Фробениуса.
Обозначим через α собственное значение,
которому принадлежит вектор
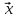 ,
следовательно, выполнено равенство
A
,
следовательно, выполнено равенство
A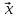 =α
=α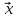 Умножая его слева на
Умножая его слева на
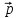 TA
и учитывая, что
TA
и учитывая, что
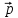 TAA=
TAA=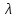 A
A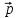 TA,
имеем:
TA,
имеем:
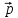 TAA
TAA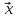 =
=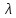 A
A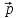 TA
TA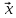 так что,
так что,
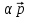 TA
TA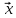 =
= A
A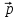 TA
TA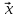 .
Поскольку по условию
.
Поскольку по условию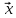 >0,
то
>0,
то
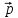 TA
TA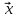
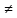 0,
так что α= λА, ч.т.д.
0,
так что α= λА, ч.т.д.
3. Докажите следующее утверждение. Пусть s и s – минимальная и максимальная суммы элементов столбцов матрицы а. Тогда число Фробениуса λА матрицы а удовлетворяет неравенству s
Док-во: выберем в качестве вектора
Фробениуса
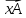 вектор, сумма координат которого равна
1, т.е.
вектор, сумма координат которого равна
1, т.е.
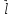 T
T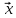 A
= 1
A
= 1
По определению имеем A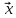 A=λA
A=λA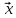 A
Умножая это равенство слева на
A
Умножая это равенство слева на
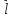 T
и учитывая, что
T
и учитывая, что
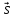 =
=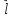 TA,
получим
TA,
получим
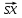 A
= λА(
A
= λА(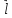 T
T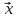 A),
поэтому λА =
A),
поэтому λА =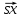 A
= s1x1+s2x2+…+snxn
отсюда следует, что s(x1+…+xn)
A
= s1x1+s2x2+…+snxn
отсюда следует, что s(x1+…+xn)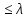 A
A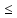 S(x1+…xn).
Учитывая, что сумма координат вектора
xA
равна 1, из неравенства получаем s
S(x1+…xn).
Учитывая, что сумма координат вектора
xA
равна 1, из неравенства получаем s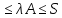
4. Запишите структурную таблицу и уравнение межотраслевого баланса Леонтьева для трехотраслевой модели экономики; укажите экономический смысл входящих в уравнение величин. Запишите формулу вычисления элементов матрицы Л. Через известные эл-ты струт. Табл. Межотр. Баланса.
|
Произв. Потребление |
Конечное потребление |
Валовой выпуск |
|
X11 X12 … X1n |
Y1 |
X1 |
|
X21 X22 … X2n |
Y2 |
X2 |
|
… |
… |
… |
|
X1n Xn2 ... Xnn |
Yn |
Xn |
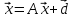 – уравнение межотраслевого баланса
(уравнение Леонтьева). Межотраслевой
баланс — экономико-математическая
балансовая модель, характеризующая
межотраслевые производственные
взаимосвязи в экономике страны. Основная
задача межотраслевого баланса состоит
в нахождении такого вектора валового
выпуска
– уравнение межотраслевого баланса
(уравнение Леонтьева). Межотраслевой
баланс — экономико-математическая
балансовая модель, характеризующая
межотраслевые производственные
взаимосвязи в экономике страны. Основная
задача межотраслевого баланса состоит
в нахождении такого вектора валового
выпуска
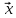 ,
который при известной матрице прямых
затрат A обеспечивает заданный вектор
конечного продукта
,
который при известной матрице прямых
затрат A обеспечивает заданный вектор
конечного продукта
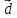 .
Зная матрицу А и вектор
.
Зная матрицу А и вектор
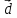 остаётся решить уравнение
остаётся решить уравнение
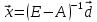 .
.
5. Сформулируйте и докажите первый критерий продуктивности
Матрица А=>0 продуктивна тогда и только
тогда, когда матрица
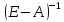 существует
и неотрицательна. Пусть существует
существует
и неотрицательна. Пусть существует
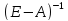 =>0,
тогда x=(E-A)-1y,
где оба множителя >0, следовательно,
x=>0, значит матрица
продуктивна. Пусть А продуктивна.
(E-A)x=e1,
значит с1=>0, (E-A)x=e2,
значит с2=>0, следовательно,
(с1,с2,cn)=C=>0.
(E-A)C=E=>C=(E-A)-1=>0
=>0,
тогда x=(E-A)-1y,
где оба множителя >0, следовательно,
x=>0, значит матрица
продуктивна. Пусть А продуктивна.
(E-A)x=e1,
значит с1=>0, (E-A)x=e2,
значит с2=>0, следовательно,
(с1,с2,cn)=C=>0.
(E-A)C=E=>C=(E-A)-1=>0
6. Докажите, что если неотрицательная квадратная матрица продуктивна, то ее число Фробениуса меньше 1
Матрица А≥0 называется продуктивной,
если для любого вектора
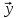 ≥0
существует решение
≥0
существует решение
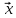 ≥0
уравнения
≥0
уравнения
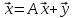
Пусть матрица А – неотрицательна и продуктивна.
Тогда для любого неотрицательного
вектора
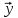 существует решение
существует решение
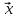 ≥0
уравнения
≥0
уравнения
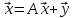
Пусть
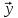 >0,
тогда, очевидно,
>0,
тогда, очевидно,
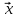 >0.
Умножив
>0.
Умножив
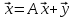 слева еа левый вектор Фробениуса
слева еа левый вектор Фробениуса
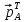 и учитывая, что
и учитывая, что
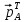 A=
A=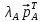 ,
то получим
,
то получим
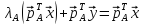
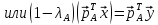
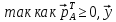 >0,
>0,
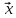 >0,
то
>0,
то
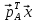 >0,
>0,
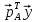 >0. Поэтому из последнего равенства
вытекает, что
>0. Поэтому из последнего равенства
вытекает, что
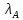 <1.
<1.
