Теорема (Крамера). Якщо визначник системи не дорівнює нулю, то система має єдиний розв’язок, який знаходиться за формулами:

.

Теорема (Кронекера-Капеллі). Система лінійних рівнянь сумісна тоді і лише тоді, коли ранг розширеної матриці системи дорівнює рангу матриці системи: .

Якщо =n система визначена

Якщо <n система невизначена

Якщо система несумісна

Довжина вектора знаходиться за формулою .

Якщо вектори задані своїми координатами, то .

Координати вектора

Умова колінеарності двох векторів = (x₁, y₁, z₁) і =(x₂, y₂, z₂),

.

Умова перпендикулярності = (x₁, y₁, z₁) і =(x₂, y₂, z₂),

х₁*х₂+у₁*у₂ +z₁*z₂ =0

Скалярним добутком двох векторів і називається число, яке дорівнює добутку довжин цих векторів на косинус кута між ними:

.

Проекція вектора на вектор та кут між ними визначаються

.

Орт вектора:

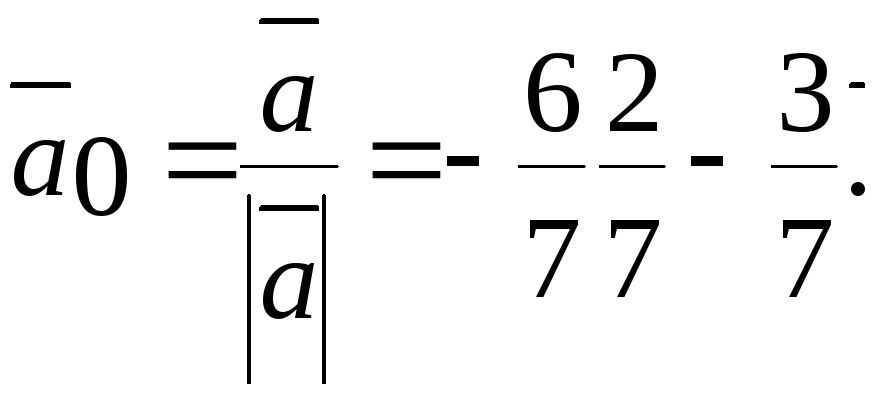
Знаходження напрямних косинусів вектора

Аналітична геометрія на площині

A(x-x₀)+B(y-y₀)=0 – рівняння прямої, яка проходить через точку М(x₀,y₀) перпендикулярно до вектора (до нормального вектора);

– рівняння прямої, яка проходить через точку М₀(x₀,y₀) паралельно напрямному вектору (канонічне рівняння);

– рівняння прямої, яка проходить через дві дані точки М₁(x₁,y₁) і М₂(x₂,y₂).

Кут між прямими

Якщо задані рівняння прямої Ax+By+C=0 і точка M₀(x₀,y₀), то відстань від цієї точки до даної прямої обчислюється за формулою

^.

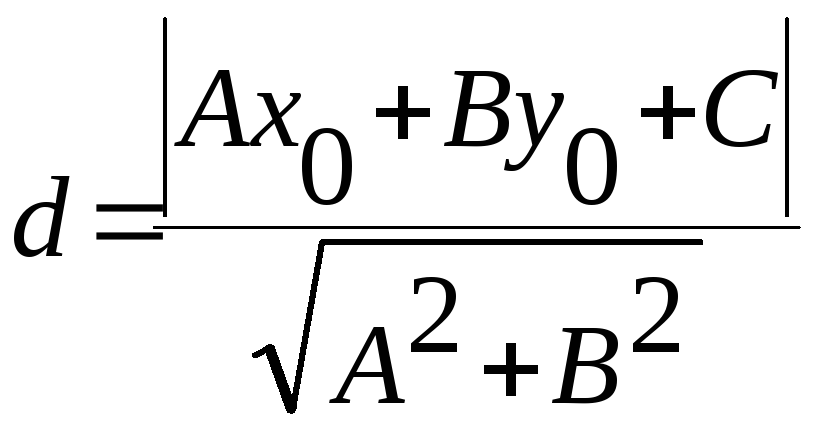Аналітична геометрія у просторі

A(x-x₀)+B(y-y₀)+C(z-z₀)=0 – рівняння площини, яка проходить через задану точку M₀(x₀,y₀, z₀,) перпендикулярно до нормального вектора :

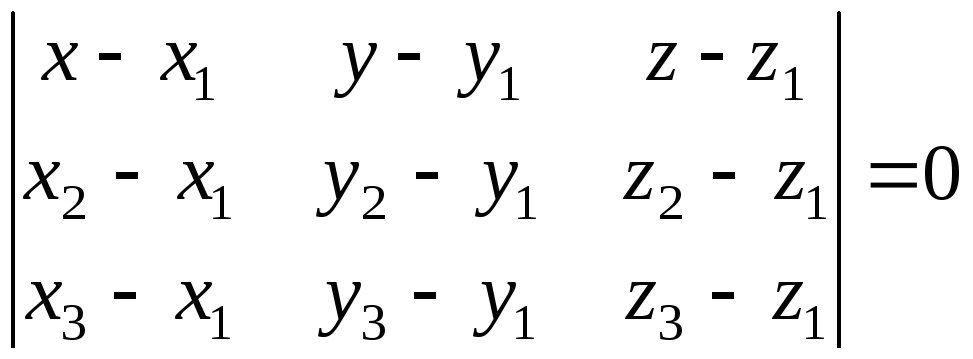– рівняння площини, яка проходить через три задані точки М₁(x₁,y₁, z₁) і М₂(x₂,y₂, z₂), М₃(x₃,y₃, z₃).

Умова паралельності двох площин A₁x+B₁y+C₁z+D₁=0 і A₂x+B₂y+C₂z+D₂=0 має вигляд , а умовою перпендикулярності цих же площин є рівність A₁ A₂+ B₁ B₂+ C₁ C₂=0.

Кут між двома даними площинами визначається за формулою

.

Відстань від точки M₀ (x₀,y₀, z₀,) до площини Ax+By+Cz+D=0:

Лінія у просторі:

– канонічне рівняння прямої, де (x₀,y₀, z₀,) –задана точка , а вектор – напрямлений вектор прямої;

– рівняння прямої, яка проходить через дві задані точки М₁(x₁,y₁, z₁) і М₂(x₂,y₂, z₂);

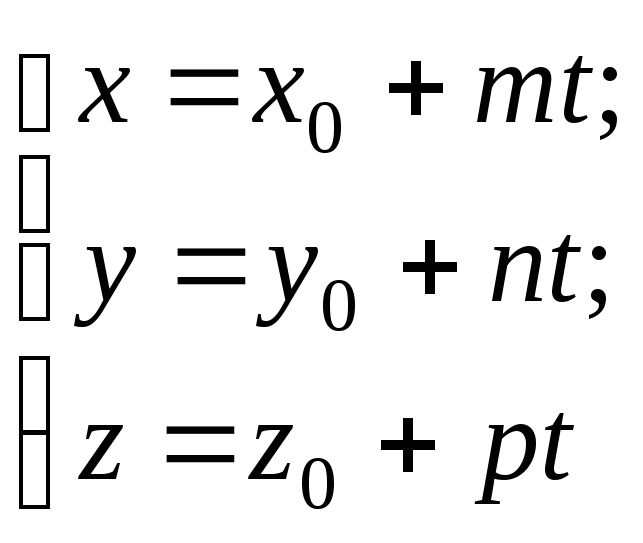- параметричні рівняння прямої у просторі, де – деякий параметр;

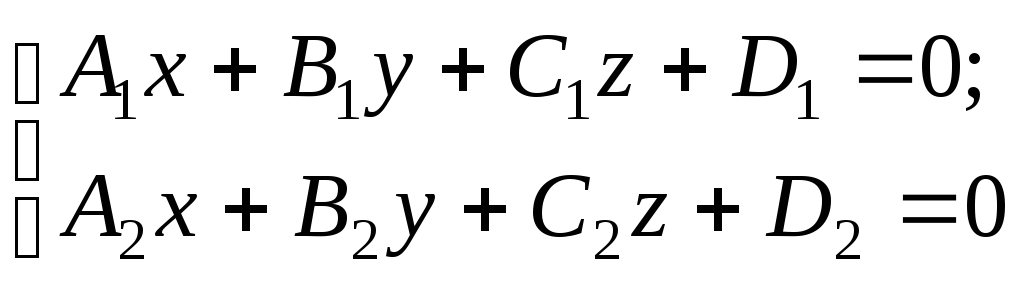– загальні рівняння прямої, коли пряма лінія визначена перетином двох площин.

Кут між прямими і обчислюється за формулою .

Умова паралельності і перпендикулярності цих прямих відповідно:

і .

Щоб знайти точку перетину прямої і площини Ax+By+Cz+D=0, слід розв’язати сумісно ці три рівняння.

ЗАДАЧА КОШИ:

Перша особлива границя:

Наслідки першої особливої границі:

sinxx (x0)

tgxx (x0)

arcsinxx (x0)

arcsin²3x(3x)² (x0)

arctgxx (x0)

1-cosx  (x0)

Друга особлива границя:

Наслідки

ln(1+x)x (x0)

log(1+x)

e^x-1x  (x0)

a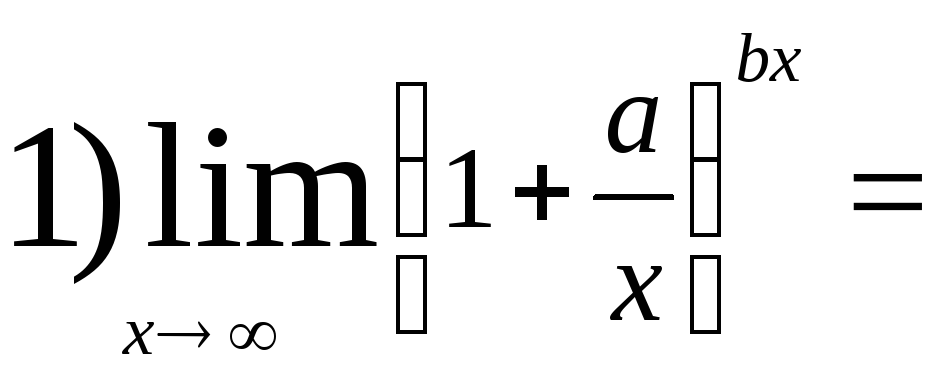^x-1 x  lna (x0)

е^ab

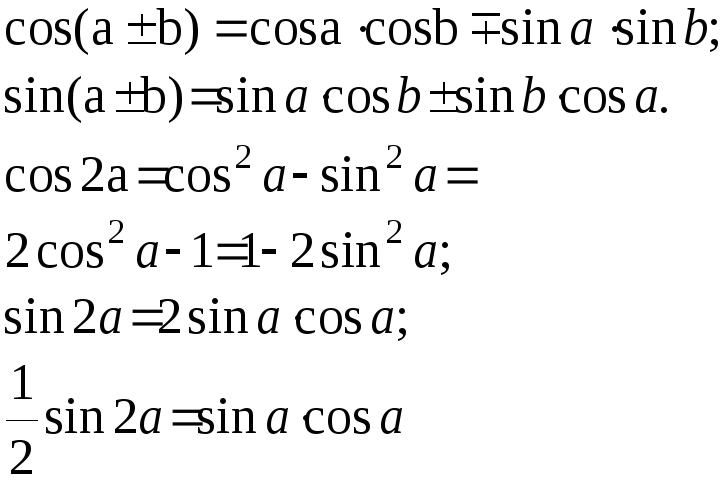
Таблиця похідних основних елементарних функцій

1.(x^m) = mx ^m-1 ;

2.(e^x)= e^x ;

2.

2.

2.

3. (lnx)=

4. (sinx)=cosx ;

5. (cosx)=-sinx ;

6. (tgx)=1/cos²x ;

7. (ctgx)=-1/sin²x ;

8. (arcsinx)=

9. (arccosx) =-

10. (arctgx) =

11. (arcctgx) =-

Основні правила диференціювання

1)С’=0;  2)x’=1;  3)(u  v)’=u’ v’; 4)(Cu)’=Cu’;

5)(uv)’=u’v+uv’; 6)

7)якщо y=f(u), u=u(x), тобто y=fu(x), де функції f(u)та u(x)мають похідні, то y’_x = y’_uu’_x (правило диференціювання складної функції).

Таблиця основних невизначених інтегралів

1. 

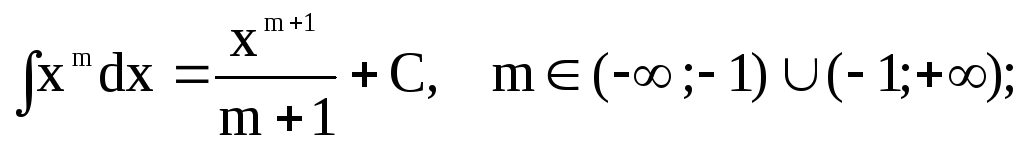
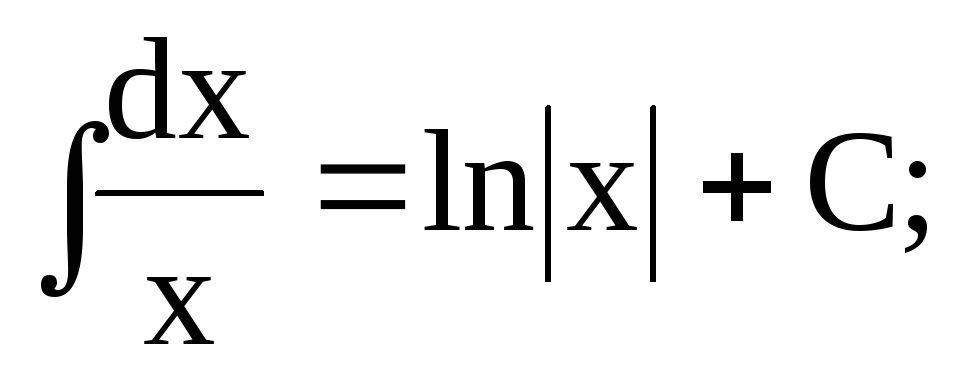
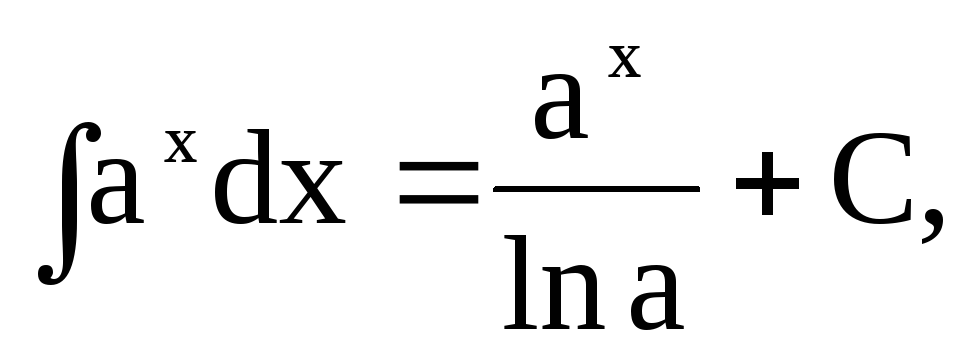2. зокрема,

3. 

4. 

5. 

6. 

7. 

8. 

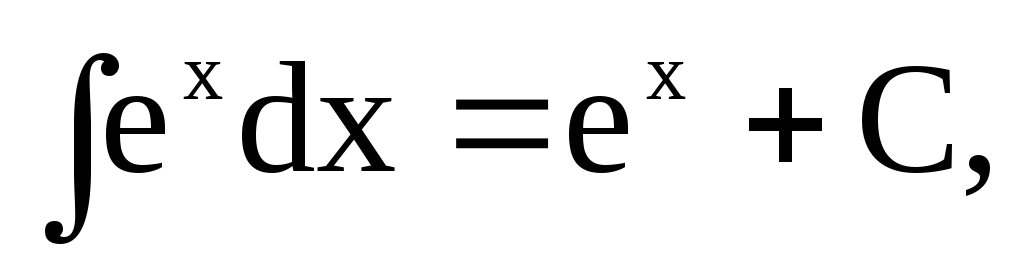
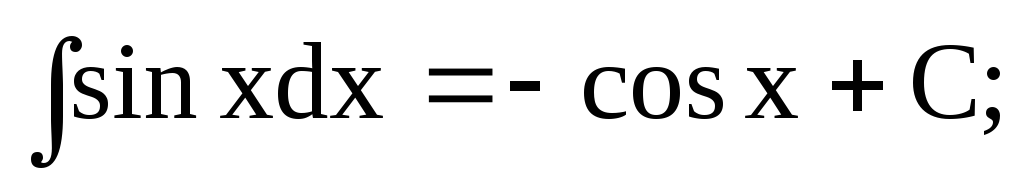
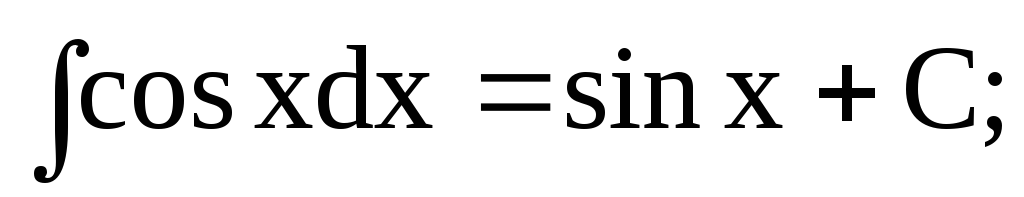
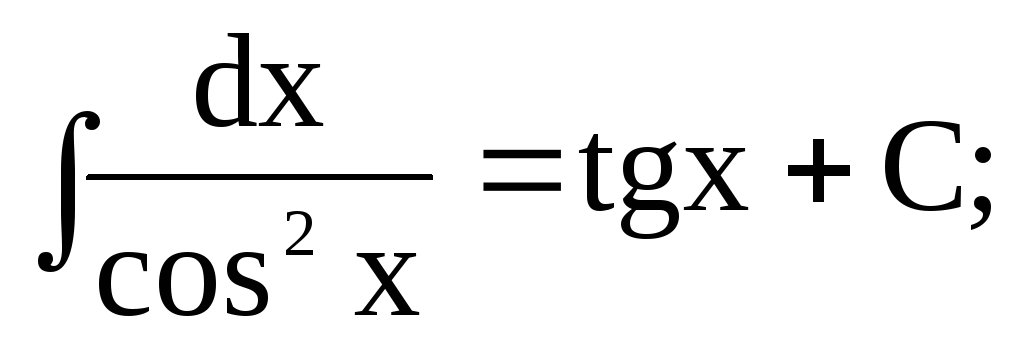
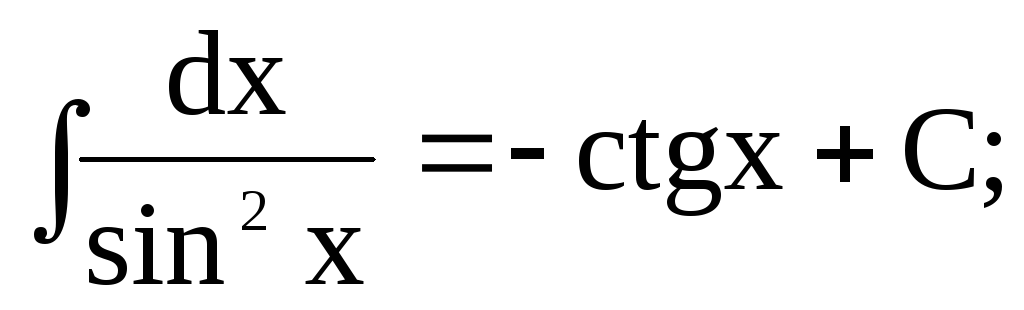
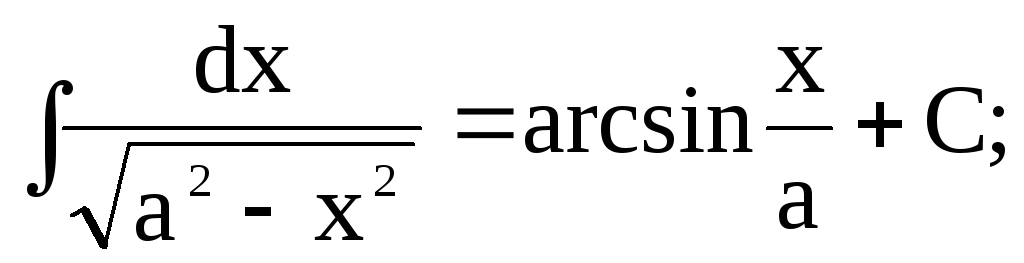
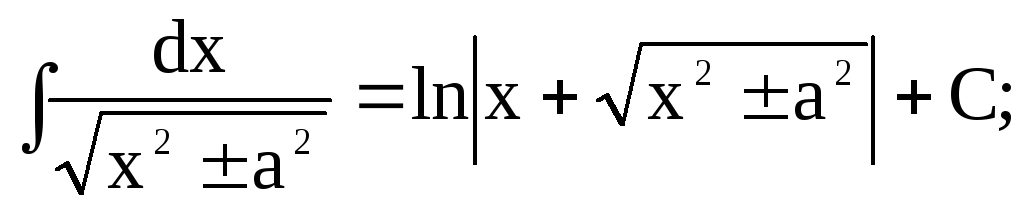
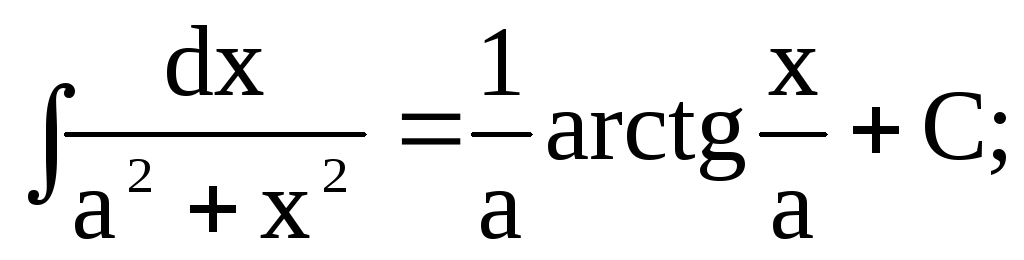
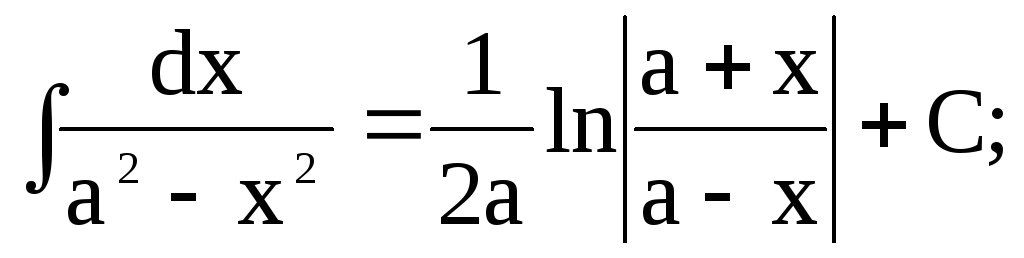
Метод інтегрування частинами

Формула Ньютона - Лейбніца

=-=│.

Метод інтегрування частинами. Формула інтегрування частинами для визначеного інтеграла має вигляд:

Схема дослідження функції на монотонність та екстремуми

1) D(y);

2) y´;

3) знайти критичні точки;

4) визначити проміжки знакосталості y´ Þ встановити проміжки монотонності y;

5) прослідкувати за зміною знака y´ при переході через критичні точки Þ встановити точки екстремуму.

Рівняння дотичної

1) у-у₀=f ’(х₀)(х-х₀) в т. М (х₀;у₀);

2) у₀=f(х₀); (число)

3) f ’(х); (вираз)

4) f ’(х₀); (число)

Рівняння у=kх±b, k= tg a

Градієнт ф-ї Z в т.М(х₀;у₀):

Градієнт ф-ї в даній т. вказує напрям і велич найб швидкості зростання цієї ф-ї в указ. точці:

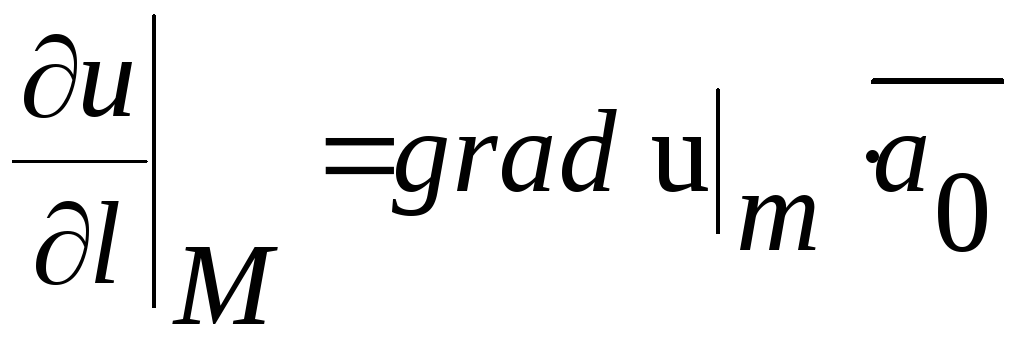
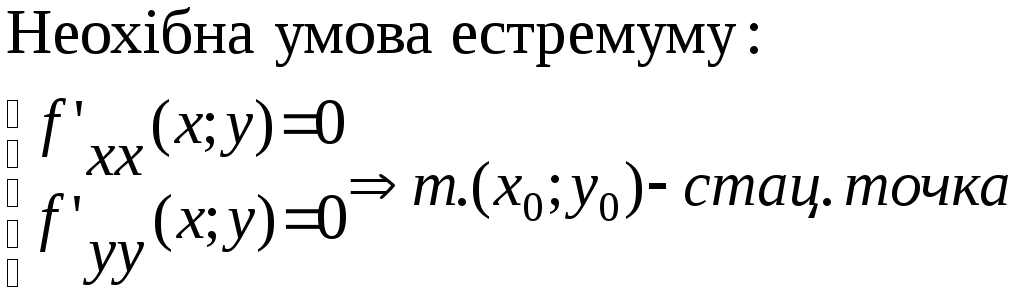
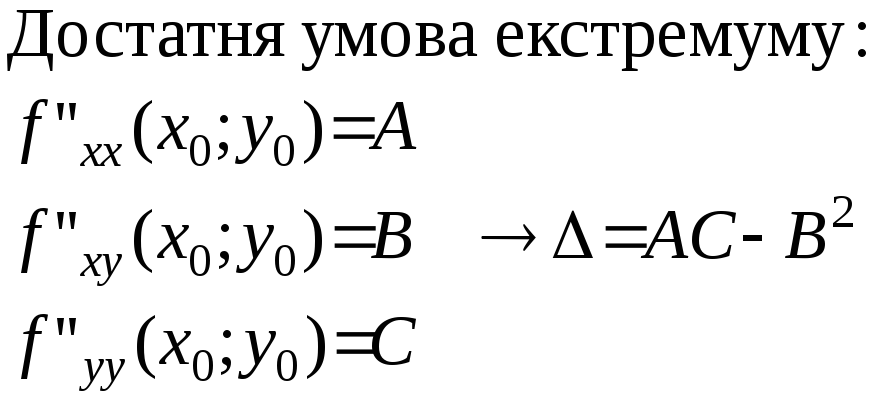
Якщо ∆>0, то (х,у)-т. екстремуму А>0-мінім, А<0-макс.

∆<0, то (х,у)- не т. екстремуму, ∆=0-потрібні подальші дослідження

Приклади розв’язання основних типів екзаменаційних задач

1. Розв’язати систему лінійних рівнянь за правилом Крамера.

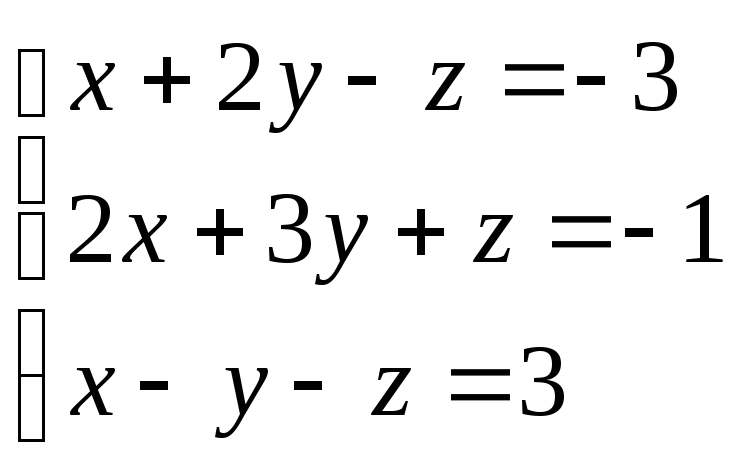
Складемо матрицю системи рівнянь, обчислимо визначник системи та додаткові визначники:

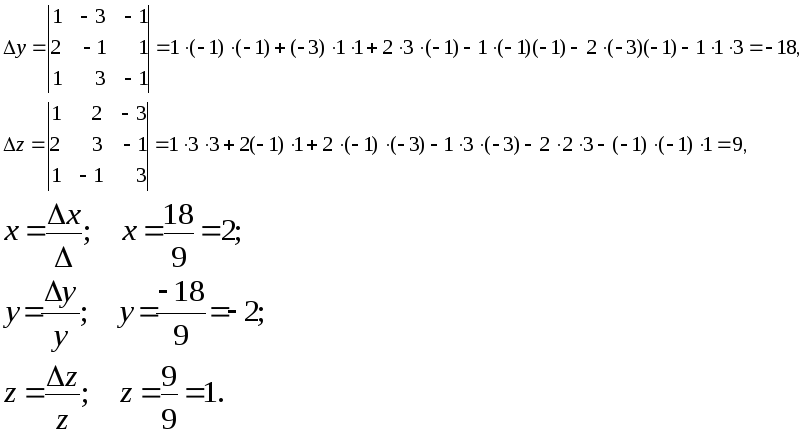
Відповідь: х = 2 ; y = 2 ; z = 1.

2. Знайти довжину вектора , якщо відомі координати точок А(2; -1), В(-3; 0), С(5; -2).

1. Якщо вектор 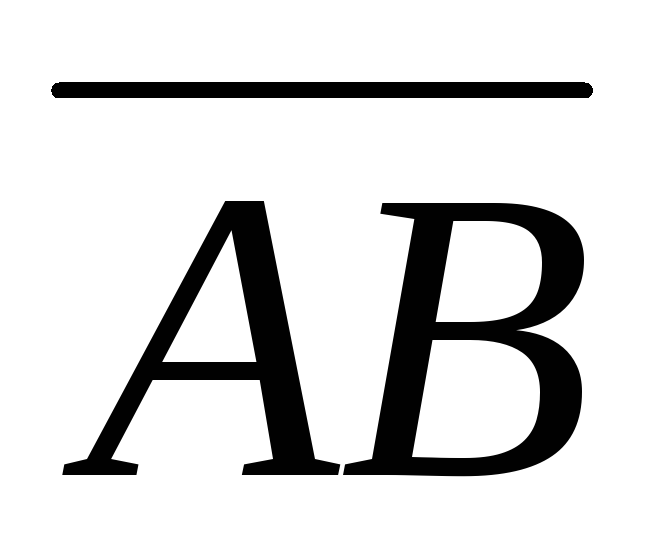має своїм початком точку А(х₁; у₁; z₁), а кінцем точку В(х₂; y₂; z₂), то кооординати вектора 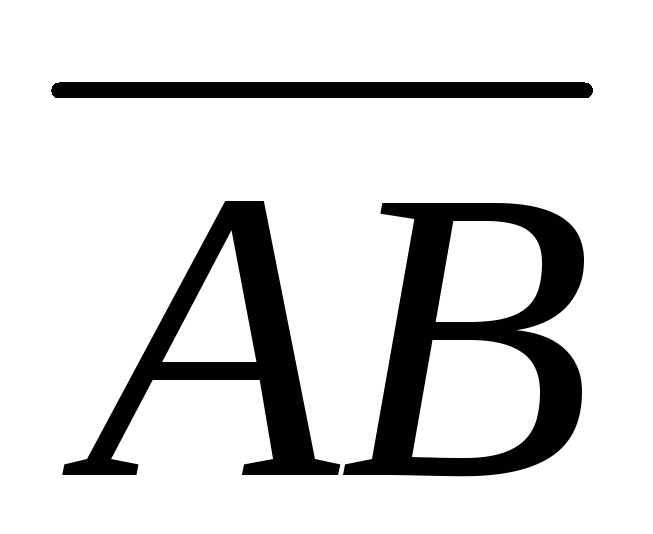обчислюються за правилом:

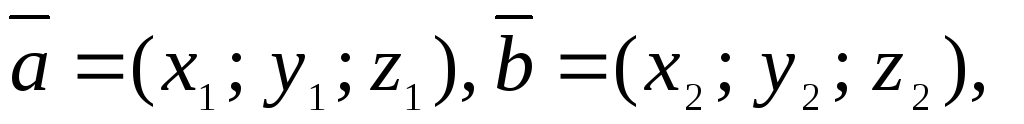2. Якщо то

3)Якщо то довжина . Тоді

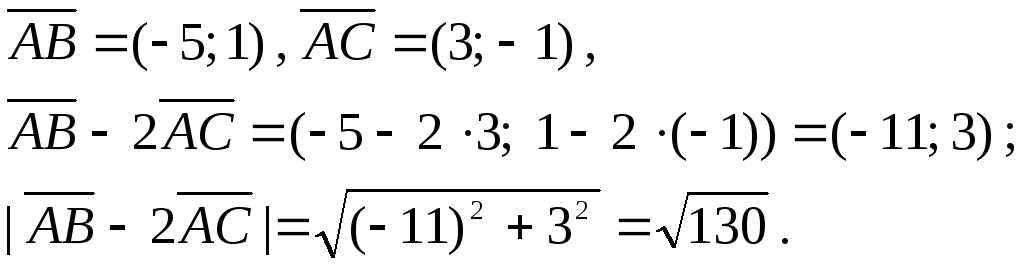
3. Знайти орт вектора

,

Тоді

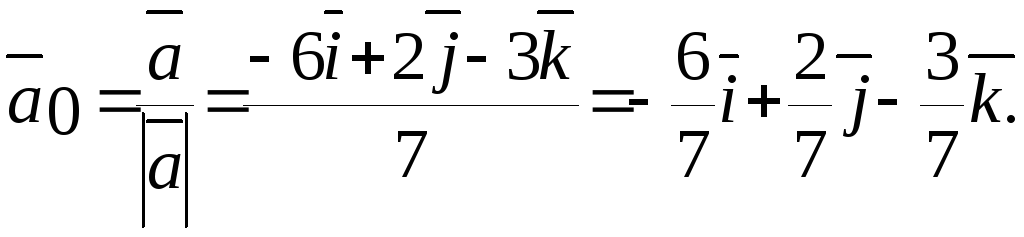
Відповідь:

4. У трикутнику з вершинами А(2;-1;3), В(-2;2;5), С(1;2;3) знайти кут при вершині А.

тоді

cosj=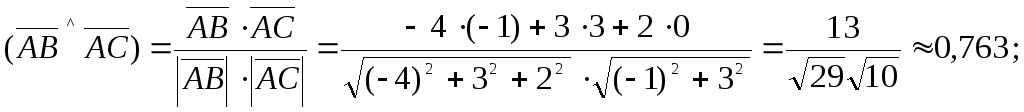

j » arccos 0,763 »40°18¢.

5. Знайти точку D так, щоб чотирикутник АВСD був паралелограмом, якщо

А(-2; 0), В(1; -3), С(2; 5).

Розв¢язання:

Якщо АВСD- паралелограм, то а два вектори рівні, якщо рівні відповідні координати. Позначимо через х,у невідомі координати точки D. Тоді

З умови рівності координат маємо: 2 –х = 3, 5-у =-3, звідси х = -1, у = 8.

Отже, одержали координати точки D (-1; 8).

6. Скласти рівняння прямої, що проходить через точки М(-1; 3) та N(2;5)

Скористаємося рівнянням прямої на площині, що проходить через точки М₁(х₁; у₁)та М₂(х₂; у₂): .

Підставляючи в це рівняння наші дані, одержуємо

або .

Рівняння має вигляд 2х –3у +11= 0.

Корисно перевірити, що рівняння складено вірно. Для цього достатньо показати, що координати точок М та N задовольняють рівнянню прямої. Дійсно, рівності

2(-1)-3·3+11= 0, 2·2- 3·5 +11=0 виконуються тотожно.