Использование кванторов в подзапросах.

В SQL предусмотрены следующие кванторы:

1. ЕXISTS - квантор существования; 2) ANY - любой; 3) SOME - некоторый; 4) ALL - все.

8.3 Динамика популяции при отсутствии и наличии смертности

Рассмотрим некоторое сообщество живых существ - популяцию. Обозначим численность популяции, т.е. количество особей, входящих в нее, через n. Разумеется, n является целым числом и может изменяться только скачкообразно, как минимум, на единицу. Однако при больших значениях n эти скачки можно считать достаточно малыми, по сравнению с объемом популяции, что позволяет считать число n изменяющимся непрерывно. Изучим процесс размножения популяции. Здесь возникает проблема усреднения по времени. Очевидно, что потомство появляется на свет не непрерывно, а через конечные промежутки времени. Большинство диких животных дает потомство один раз в год. Иначе говоря, время в живой природе изменяется дискретно, скачками. Однако на больших интервалах можно усреднять и время, считая его непрерывным. После всех сделанных оговорок, считая и объем популяции, и время величинами непрерывными, можно применить к изучению вопроса об изменении численности популяции теорию дифференциальных уравнений. Скорость изменения непрерывной функции непрерывного времени n=n(t) находится как производная: dn/dt. Остается выяснить, от чего зависит эта скорость. Начнем с предположения, что скорость изменения объема популяции пропорциональна этому объему. Иначе говоря, количество потомков пропорционально количеству родителей. Обозначая коэффициент пропорциональности через m имеем: (2.1.1)Это одно из самых простых и известных дифференциальных уравнений; его решение будет: (2.1.2)где n₀ - начальный объем популяции. Проанализируем полученный результат. Рассмотрим произвольный момент времени t и какое-то приращение времени t. Вычислим следующее отношение: (2.1.3)

Таким образом, через равные промежутки времени t объем популяции изменяется одинаковым образом в k раз. Графически этот результат (при m=ln2 и n₀=1) представлен на рис.1.

Известны и некоторые современные проблемы, связанные с полученными результатами. Обратим внимание, что время на рис.1 изменяется по закону арифметической прогрессии: 0, 1, 2, 3,..., а объем популяции - по закону геометрической прогрессии: 1, 2, 4, 8,...

В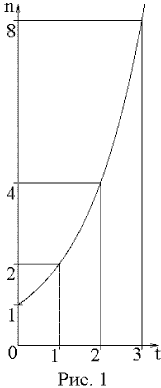первые подобное экологическое взаимодействие двух прогрессий - арифметической и геометрической - заметил английский священник и философ Мальтус. Он обратил внимание на то, что объем населения Земли растет в геометрической прогрессии (т.е. по закону (2)), а рост производства продуктов питания - в лучшем случае в арифметической прогрессии, т.е. гораздо медленнее. Отсюда Мальтус сделал естественный вывод о недопустимости бесконтрольного увеличения населения Земли, неизбежно влекущего за собой массовый голод и другие проблемы перенаселения. В качестве «естественного» регулятора численности населения Мальтус предложил... войны.

Влияние смертности на динамику популяции. Действительно, в модели, описанной в предыдущем параграфе, смертность не учитывалась, т.е. предполагалось одновременное существование предков и потомков независимо от возраста. Кроме того, подразумевалось, что предки любого возраста продолжают производить потомство наравне со своими детьми.Пусть коэффициент пропорциональности в (1.1) имеет вид: m=. Положительную его часть  будем называть коэффициентом рождаемости, отрицательную: -  к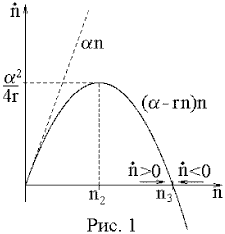оэффициентом смертности. Если  и  - константы, то такое структурирование коэффициента m мало что меняет. При > имеем m>0 и прежний экспоненциальный рост объема популяции. Это случай, когда рождаемость превышает смертность. При < будет m<0 и решение (1.2) опишет новую ситуацию - экспоненциальное убывание объема популяции. Это случай преобладания смертности над рождаемости. Рассмотрим более сложную и, в то же время, естественную ситуацию. При чрезмерном росте объема популяции возникают проблемы жизнеобеспечения, связанные, например, с нехваткой продовольствия или чего-то еще, не менее важного. Поэтому коэффициент смертности может возрастать с увеличением численности популяции. Предположим, например, что он пропорционален n, т.е. Тогда и вместо уравнения (1.1) получаем: (2.2.1)Это уравнение уже несколько более сложное, чем (1.1). И хотя его интегрирование все еще достаточно просто, полезно предварительно рассмотреть фазовый портрет. Поскольку мы имеем одно дифференциальное уравнение первого порядка, то в осях само это уравнение и является формулой фазовой кривой (рис.1). Это парабола, пересекающая ось n в точках n₁=0 и n₃=/r. Для сравнения изображена и фазовая кривая при отсутствии смертности (r=0), т.е. прямая . В соответствии с этой прямой скорость роста объема популяции растет вместе с величиной объема. Наличие смертности ограничивает скорость максимальным значением , достигаемом при n₂=/(2r). С дальнейшим увеличением n скорость роста начинает падать, обращаясь в ноль при n₃=/r. Это значение объема является равновесным. При n<n₃ имеем , а при n>n₃ - . Следовательно, при любых отклонениях от значения n=n₃ объем популяции стремится вернуться к этому значению. Значит, это устойчивое положение равновесия.Как видим, и здесь фазовый портрет дает значительную информацию о поведении системы. Наличие этой информации облегчает и исследование решения уравнения (1). Разделяя в (1) переменные и интегрируя получаем:

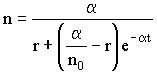(2.2.2)

где n₀ - по-прежнему начальное значение n при t₀=0.

На рис.2 приведены соответствующие кривые для ряда значений n₀. П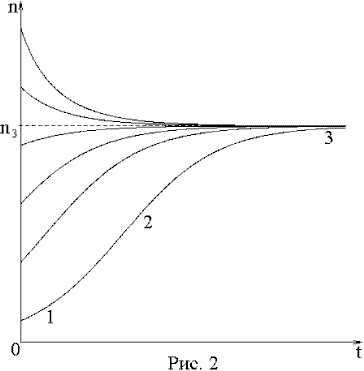ри n<n₃ наблюдается рост, а при n>n₃ - убывание n. Во всех случаях значение n асимптотически стремится к значению n₃. S-образные кривые, изображенные на рис.2, впервые исследовал Ферхюльст, в связи с чем их называют логистическими кривыми Ферхюльста.

Собственно, S-образной является только самая нижняя из кривых, изображенных на рис.2. Рассмотрим ее подробнее. При малых значениях n₀ коэффициент пропорциональности m приблизительно равен n (рис.1). Это обеспечивает экспоненциальный рост объема популяции (участок 1 на рис.2). Он характерен тем, что ресурсы популяции практически полностью расходуются на воспроизводство. С ростом n становится заметной смертность. Иначе говоря, часть популяции теряет репродуктивные свойства. В окрестности максимального значения скорости график n=n(t) приобретает приблизительно прямолинейную форму (участок 2 на рис.2). С дальнейшим увеличением n скорость роста приближается к нулю и объем популяции стабилизируется вблизи значения n₃ (участок 3). Теперь смертность уравновешивает рождаемость. Эти результаты вполне соответствуют полученным при рассмотрении фазового портрета. Они наглядно показывают разные фазы развития популяции. Стабилизацию обеспечивает уменьшение коэффициента пропорциональности m до нуля. Обратим внимание на то, что полученные результаты можно интерпретировать по разному. При постоянном коэффициенте рождаемости  стабилизация обеспечивается тем, что коэффициент смертности растет вместе с n. Т.е., с ростом объема популяции, вымирает все большая относительная доля этой популяции (например, от нехватки продовольствия). Иначе говоря, живые существа производят явно избыточное количество потомства и значительная часто этого потомства погибает. Вместо этого можно считать, что формула отражает не рост коэффициента смертности, а уменьшение коэффициента рождаемости. Популяция ограничивает свой объем целенаправленно, уменьшая количество потомков не за счет их смерти, а за счет регулирования рождаемости. В этом случае достигается тот же результат стабилизации объема популяции, но совсем иными, чем предлагал Мальтус, методами.