Классификация особых точек

Начнем с уравнения малых свободных колебаний вблизи устойчивого положения равновесия: (3.3.1)

и проследим подробно процедуру его решения. Поскольку это линейное уравнение с постоянными коэффициентами, то его решение ищем в виде: (3.3.2) Подставляя (2) в (1) получаем, после сокращения общих множителей, характ-ское ур-е: (3.3.3) имеющее чисто мнимые корни: (3.3.4). В соотв-и с наличием двух корней имеем и два реш-я типа (2). Общее реш-е ур-я (1) является суммой двух таких частных реш-й: (3.3.5)

Оно содержит две произвольные постоянные А₁ и А₂. Во многих случаях удовлетворяются решениями типа (5) (например, в электротехнике), однако все же в большинстве случаев представление действительной величины х через функции комплексного аргумента не очень удобно. Воспользуемся тождеством Эйлера: (3.3.6). Тогда (5) можно представить в виде: (3.3.7)

В то время как А₁ и А₂ были комплексными числами, новые константы В₁ и В₂ являются действительными числами. Найдем их значения, удовлетворяя начальным условиям: при t₀=0 даны величины х₀ и v₀. Из (7) найдем: (3.3.8)

Подставляя в (7) и (8) t₀=0 получаем: (3.3.9)

Окончательно: (3.3.10)

От формы (7) (или (10)) можно перейти к более компактной форме записи решения. Пусть: (3.3.11)

Тогда (7) можно записать в виде: 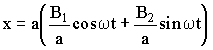(3.3.12)

Поскольку справедливо тожд-во: 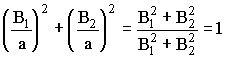(3.3.13), то сущ-т такой угол a, что: (3.3.14) и(3.3.15)

Т.о., мы видим, что чисто мнимые корни соответствуют гармоническим колебаниям. Исключая из (15) время t получаем уравнение фазовых кривых: 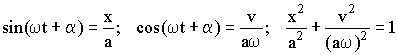(3.3.16)

Изменяя амплитуду , получаем семейство эллипсов, т.е. уже знакомую особую точку типа фокус (рис.1).

Рассмотрим, вместо (3.3.1), уравнение: (3.3.17)

Оно может описывать движение системы вблизи точки максимума потенциальной энергии и получается тем же способом, как при движении вблизи точки минимума, но с учетом того, что вторая производная не уже не положительная, а отрицательная. Вновь разыскивая решение в виде (2), получаем характеристическое уравнение: (3.3.18),

имеющее два действительных корня: (3.3.19)

Следовательно, общее решение имеет здесь вид: (3.3.20)

Действительным корням характеристического уравнения соответствует решение неколебательного типа.

Пусть при t₀=0 даны x₀ и v₀. Вычисляем: (3.3.21)

Подставляя в (20) и (21) t₀ имеем: (3.3.22)

Отсюда: 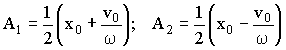(3.3.23)

В итоге из (20) получаем: 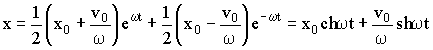(3.3.24)

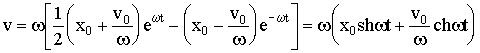
Рассмотрим следующие два случая:

1) 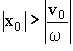. Обозначим: 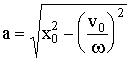(3.3.25)

Запишем выражение для х в виде: 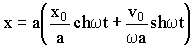(3.3.26)

Учтем, что гиперболические косинус и синус удовлетворяют тождеству: (3.3.27) Подобному же тожд-ву удовлетворяют и коэффициенты в (26): 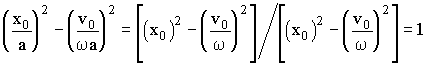(3.3.28)

Следовательно, существует такое значение a, что: (3.3.29)

Подставляя (29) в (26) получаем: (3.3.30)

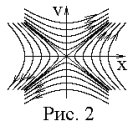
Исключим из (30) параметр t: (3.3.31)

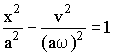
При различных значениях а получаем семейство гипербол, пересекающих ось х (рис 2).

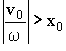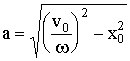
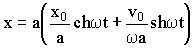2) . В этом случае имеем: (3.3.32)

Существует такое значение a, что: (3.3.33)

Следовательно: (3.3.34)

И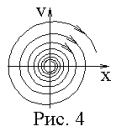сключая из (34) параметр t, получаем: (3.3.35)

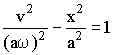
При разл. знач-х а получаем семейство гипербол, пересек-их оси (рис.2).

В целом видим, что мы опять пришли к особой точке типа седло. Она соответствует двум действит-ым и разным по знакам корням характеристического ур-я.

Дополним уравнение (1) слагаемым, учитывающим сопротивление, получая: (3.3.36) Разыскивая решение в виде (2) получаем характеристическое уравнение: (3.3.37) Его корни: (3.3.38)

Рассмотрим следующие случаи:

1) n < w. В этом случае имеем комплексные сопряженные корни: (3.3.39)

Общее решение будет: (3.3.40)

Преобразовывая выражение в скобках таким же образом, как было преобразовано выражение (5), получаем: (3.3.41)

Этим затухающим колебаниям соответствует особая точка спиралевидного вида, которая по-прежнему называется фокусом (рис.3). Заменяя в (41) знак n на противоположный, получим уже не затухающие, а раскачивающиеся колебания. Но особая точка и в этом случае называется фокусом (рис.4).

Подводя итоги по всем вариантам особых точек типа фокус, можно сказать, что они всегда соответствуют комплексным корням характеристического уравнения.

2) n > w. В этом случае оба корня (38) действительны. При этом знаку минус перед корнем соответствует отрицательный корень; т.к. подкоренное выражение меньше n, то и знаку плюс также соответствует отрицательный к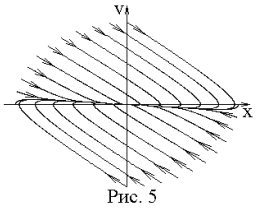орень. Введем обозначения: (3.3.42) Общее решение: (3.3.43)

Фазовая кривая с ростом t асимптотически приближается к началу координат (рис. 5). Такая особая точка называется узлом.

Если поменять знак n на противоположный, то оба корня характеристического уравнения станут положительными. В этом случае фазовый портрет будет аналогичен изображенному на рис.5, но фазовые кривые с ростом t будут удаляться от начала координат. Такая особая точка также называется узлом.

3) n = w. В этом случае корни характеристического уравнения равны между собой и решение имеет вид: (3.3.44)

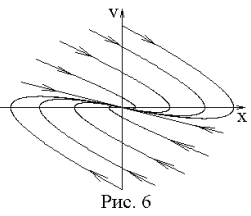
Здесь также с течением времени фазовые кривые приближаются к началу координат; поэтому и такая особая точка называется узлом (рис.6).

При противоположном знаке n фазовые кривые удаляются от начала координат, но и в этом случае особая точка называется узлом.

Подводя итоги всем рассмотренным примерам можно указать следующие признаки особых точек.

1. Если корни характеристического уравнения комплексные, то особая точка называется фокусом.

2. Если корни действительные и разных знаков, то особая точка называется седлом.

3. Если корни действительные и одинаковых знаков, то особая точка называется узлом.