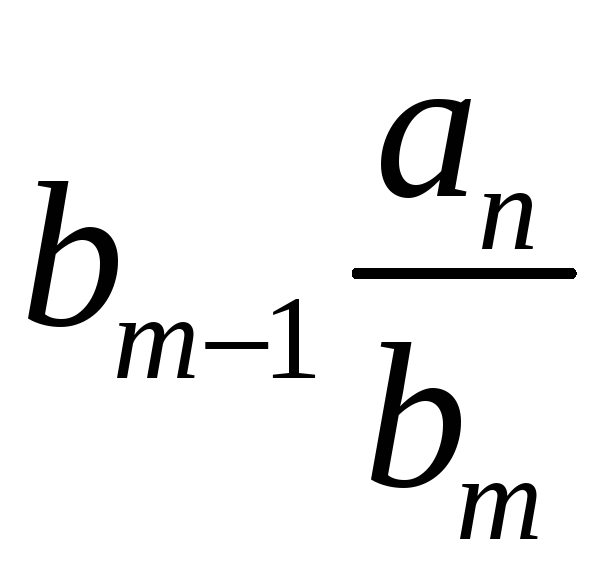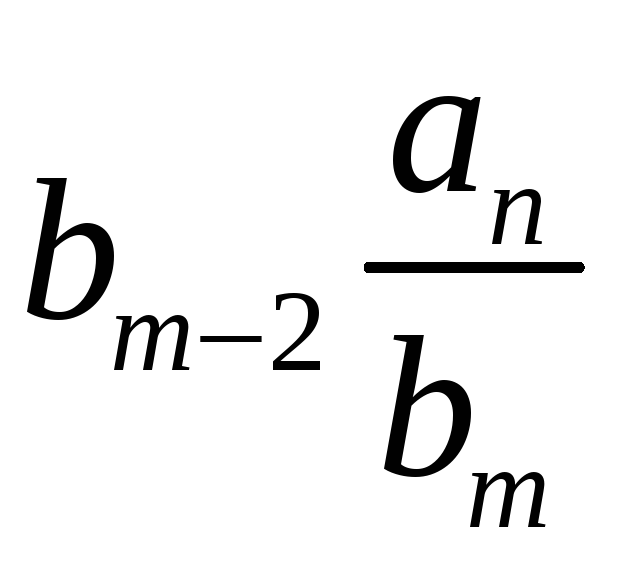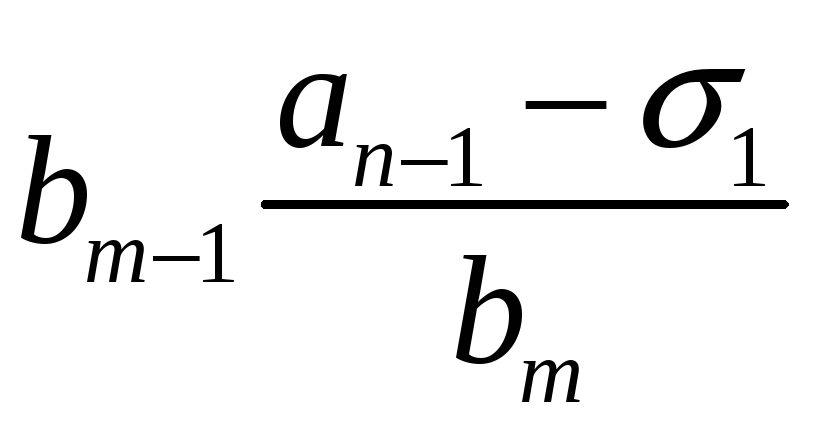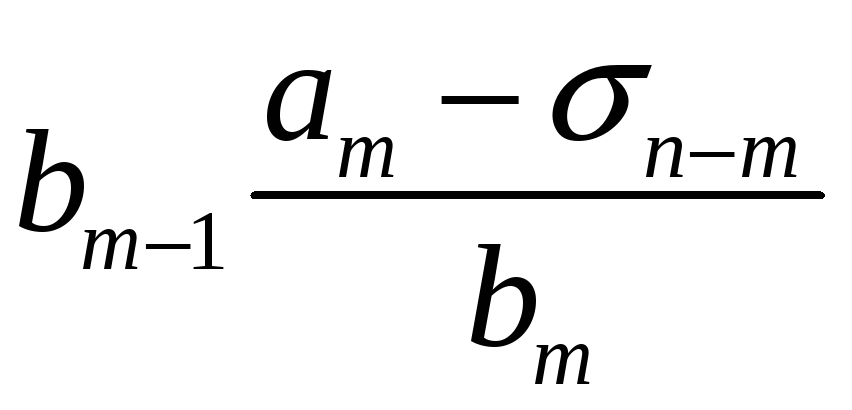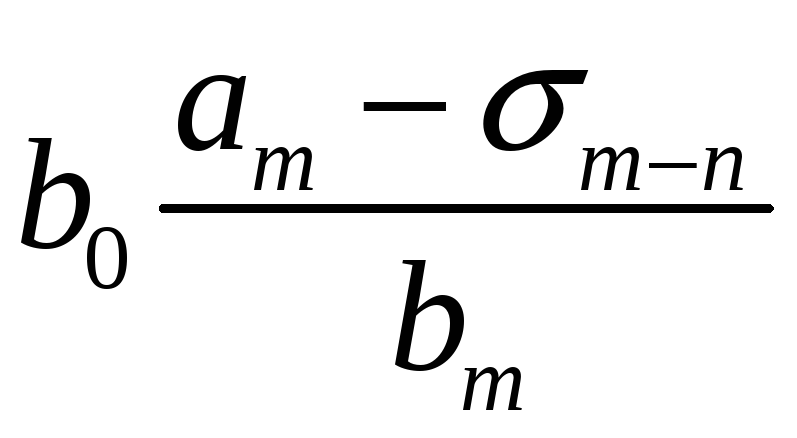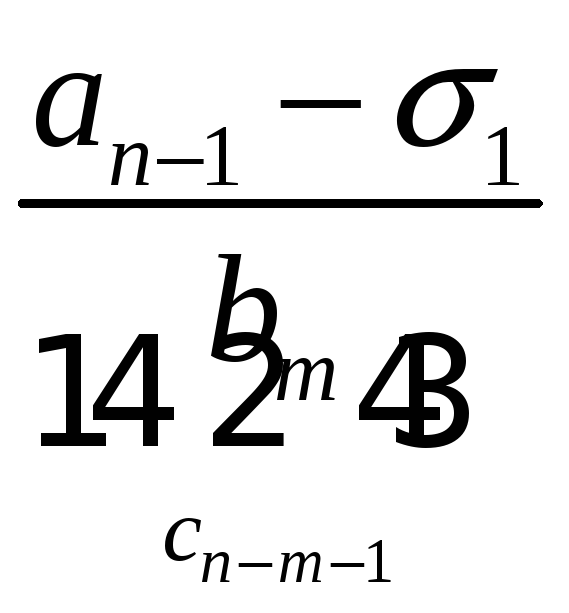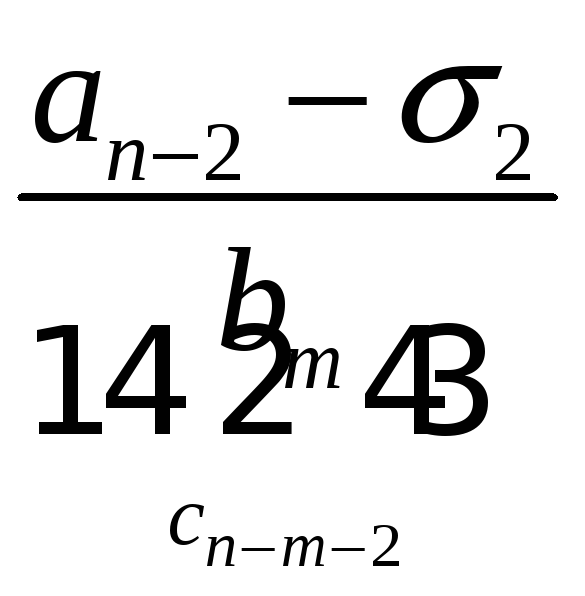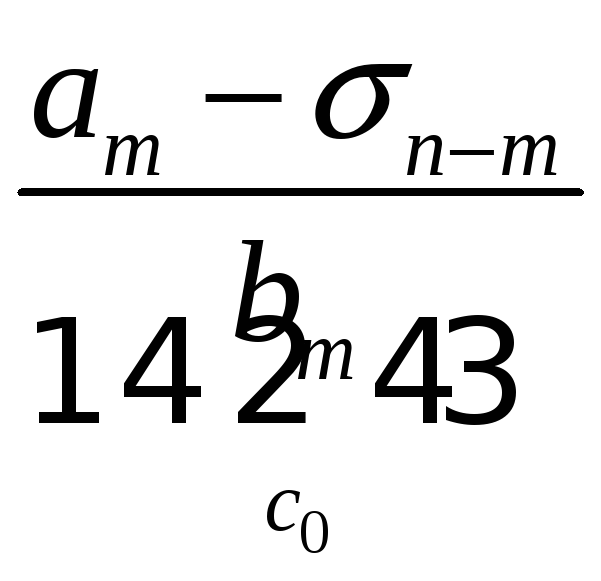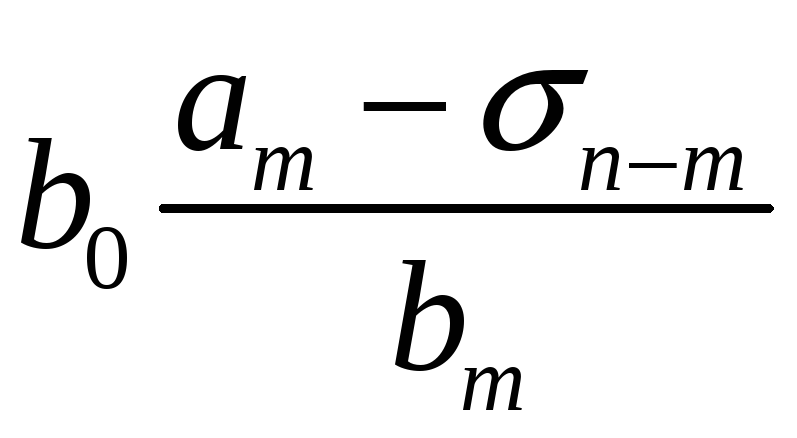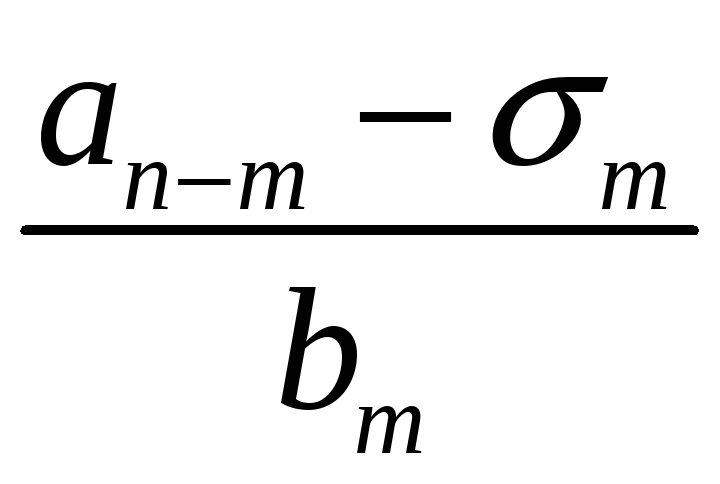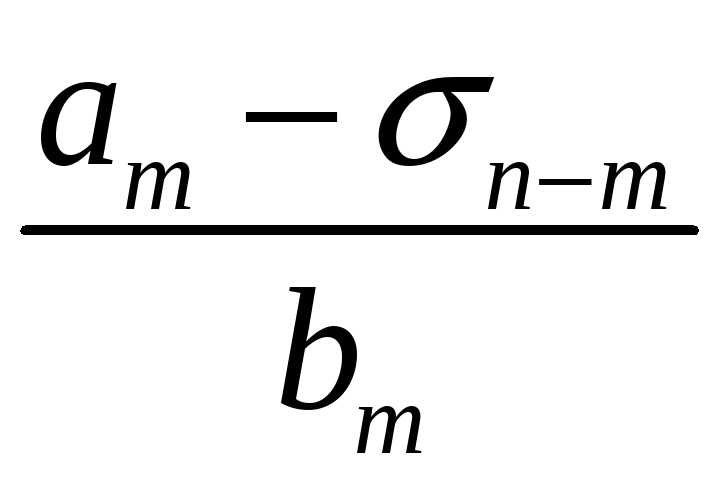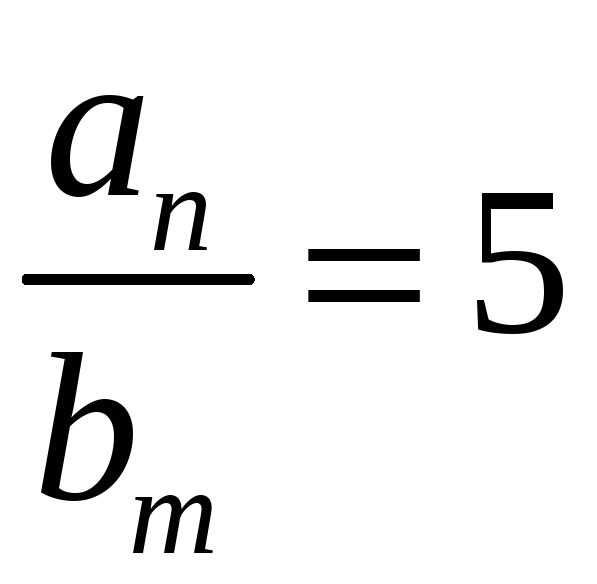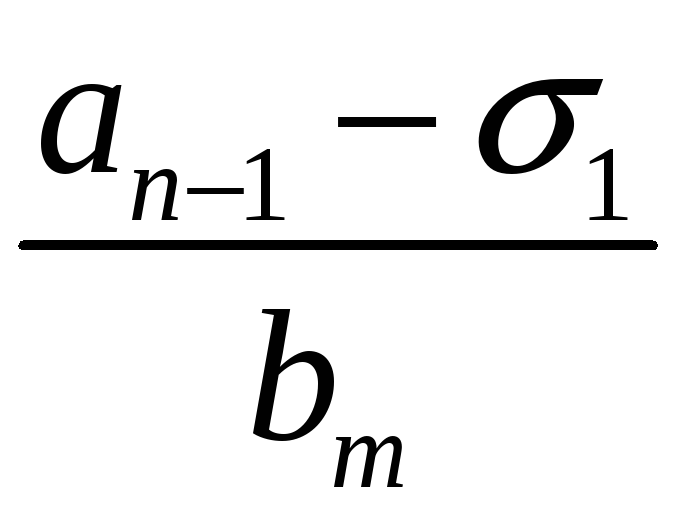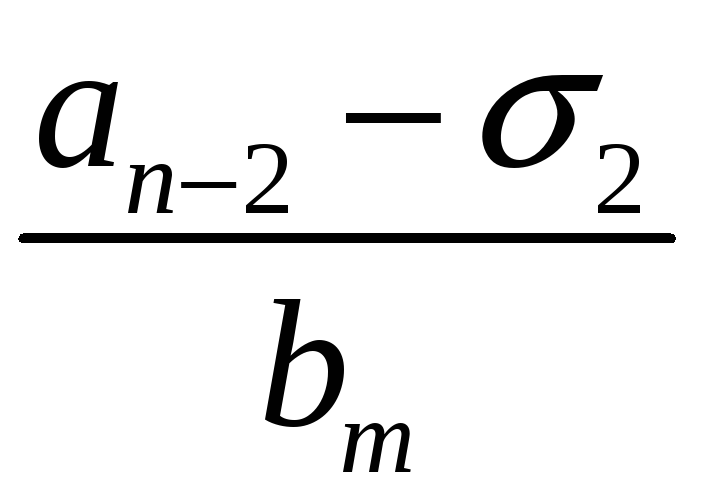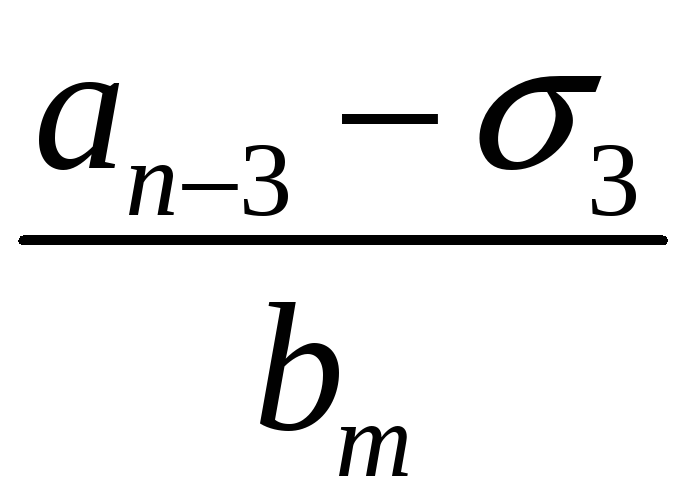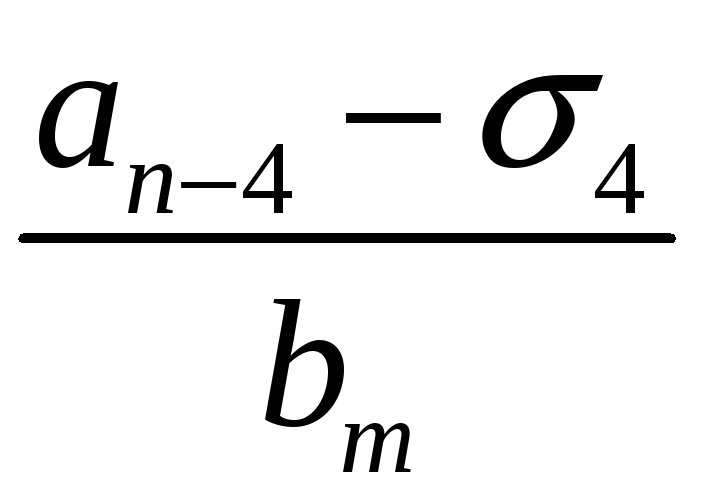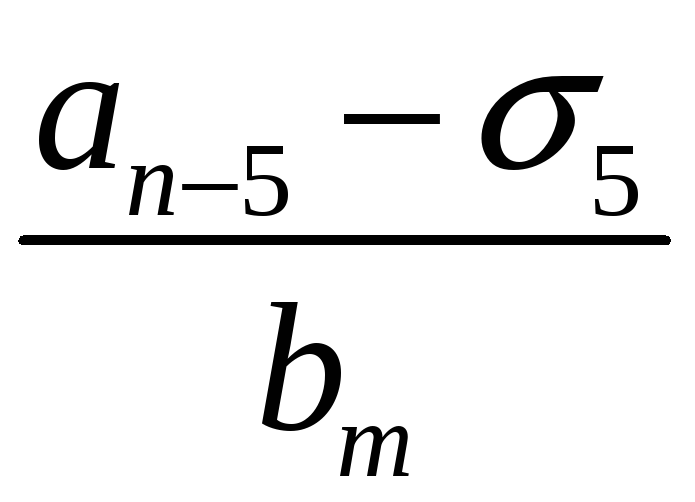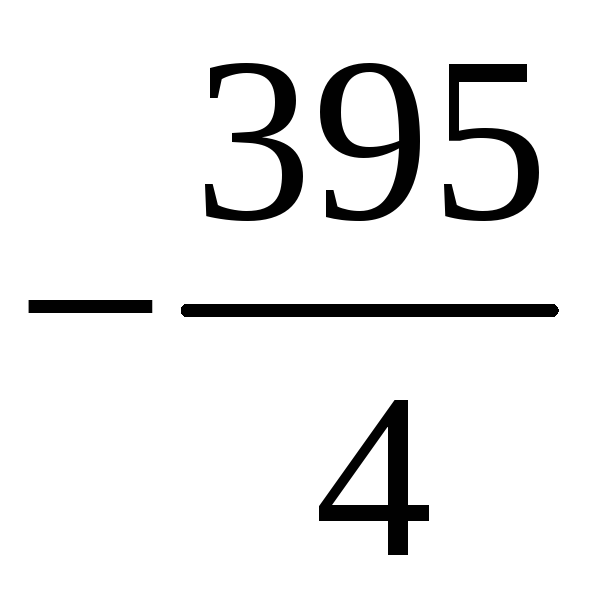Порядок числа і класу лишків за модулем. Первісні корені, існування їх та кількість за простим модулем

Нехай , і . Порядком числа а за модулем називається таке найменше натуральне число , що . Число позначають ще як і називають показником, до якого належить число за модулем . Оскільки за теоремою Ейлера , то число завжди існує і . Якщо , то число називають первісним коренем за модулем .

Якщо , то . Ця властивість дає змогу казати про порядок класу лишків, а саме: клас лишків має порядок за модулем . якщо порядок його представника за цим самим модулем дорівнює .

Якщо, то клас лишків називається класом первісних коренів за модулем .

Якщо , то числа попарно не конгруентні між собою за модулем .

Якщо — первісний корінь за модулем , тобто , то числа утворюють зведену систему лишків за модулем .

Якщо , то тоді і тільки тоді, коли . Зокрема, тоді і тільки тоді, коли .

Якщо і , то

Якщо , то .

Якщо , то .

Якщо , то .

Якщо - попарно взаємно прості числа, то. тоді і тільки тоді, коли .

.

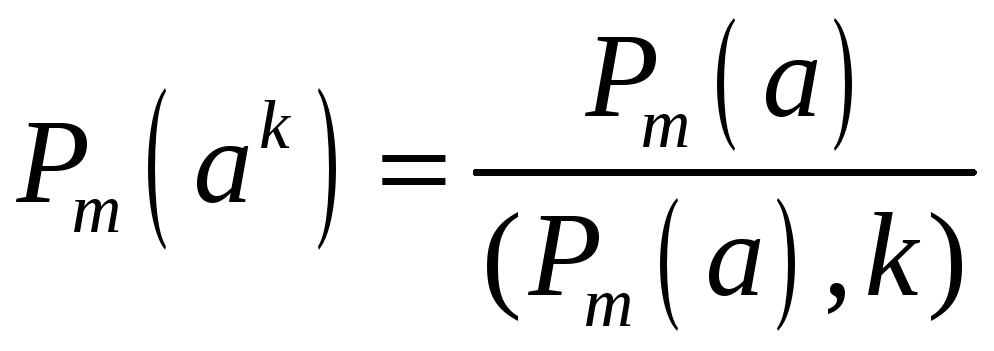Якщо, то класи лишків є різними розв'яз­ками конгруенції .

Якщо — просте число, то зазначені класи лишків вичерпують усі розв'язки даної конгруенції.

За простим модулем кожен дільник числа є порядком для класів лишків. Зокрема, існує класів первісних коренів (теорема Гаусса).

Якщо первісний корінь за простим модулем , то інші первісні корені містяться серед степенів і мають вигляд , де і .

Якщо— канонічний розклад числа , то число тоді і тільки тоді є первісним коренем за простим модулем , коли

для всіх .

Первісні корені існують тільки за модулями ; і , де - просте непарне число, а .

Нехай —первісний корінь за простим модулем . Тоді можна знайти таке число , що число , яке визначається з умови

,

не ділиться на . Відповідне число є первісним коренем за модулем при будь-якому .

Нехай і — первісний корінь за модулем . Непарне з чисел і є також первісним коренем за модулем .

Якщо і - різні прості дільники числа , то число , взаємно просте з , тоді і тільки тоді є первісним коренем за модулем ; коли

для всіх .

Індекси за простим модулем. Двочленні конгруенції за простим модулем; таблиці індексів і застосування їх.

Нехай - первісний корінь за простим модулем , і . Ціле невід’ємне число називається індексом за модулем при основі , якщо

(1)

Взагалі, довільне значення , яке задовольняє конгруенцію

, (2)

називається індексом числа за модулем при основі і позначається

. (3)

При цьому може бути й складним числом , проте

.

Означення індексу можна записати ще так:

. (4)

Користуючись цим означенням, складають таблицю Індексів за даною основою і модулем. Таблиці індексів за кожним простим модулем (не дуже великим) містять дві таблиці: одна — знаходження індексу за числом, а друга — знаходження числа за індексом (таблиця анти індексів).

Основні властивості індексів

1°. Усі індекси числа за простим модулем утворюють клас чисел за модулем . Точніше, якщо і — індекси числа за модулем (при будь-якій тій самій основі), то

.

2°. Для того щоб , необхідно і достатньо, щоб

.

Якщо значення чисел або індексів виходять за межі таблиць, то ці дві властивості дають змогу переходити до найменших невід'ємних лишків: для чисел — за модулем , для індексів — за модулем ;

3°. ;

4°. ;

5°. ;

6°. ;

7°. Якщо , то .

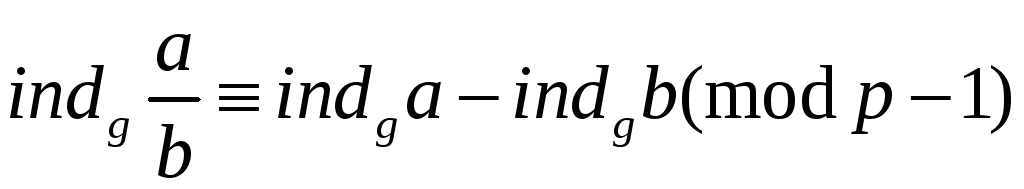Зазначимо, що перехід від конгруенції між числами до конгруенції їхніх індексів називається індексацією, а зворотний перехід –потенціюванням. Якщо задано двочленну конгруенцію

го степеня за простим модулем

,, (5)

то її розв'язок знаходять з конгруенції

(6)

Задачі рекомендовані для розв‘язування в аудиторії

1. Знайти порядок числа за модулем , якщо:

а) ; б) ;

в) ; г) .

2. Знайти порядки чисел за модулем , якщо:

а) ;

б) ;

в)

3. Скласти таблицю індексів для модуля 50, взявши за основу первісний корінь 3; з допомогою цієї таблиці розв‘язати конгруенції) ; б) .

4. Користуючись таблицями індексів, розв‘язати конгруенції:

а) ; б) ;

в) 4 г) ;

д) ; е) ;

є) ; ж) ;

5. Скільки розв‘язків мають такі конгруенції:

а) ; б) ;

в) ; г) ;

д) ?

6. Розв‘язати двочленні конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) ;

є) ; ж) ;

з) ; к) .

7. Розв‘язати конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) .

8. Знайти найменшу натуральне число , яке задовольняє такі конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) .

Задачі рекомендовані для розв‘язування дома

1. Знайти порядок числа за модулем , якщо:

а) ; б) ;

в) ; г) .

2. Знайти порядки чисел за модулем , якщо:

а) ;

б) .

3. Знаючи, що 2 є первісним коренем за модулями 101 і 163, розв‘язати показникові конгруенції:

а) ; б) .

4. Скласти таблицю індексів для модуля 27, взявши за основу первісний корінь 2; з допомогою цієї таблиці розв‘язати конгруенції) ; б) .

5. Визначити число розв‘язків конгруенцій:

а) ; б) ; в) .

6. Користуючись таблицями індексів, розв‘язати конгруенції:

а) ; б) ;

в) ; г) .

7. Розв‘язати конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) ;

є) ; ж) ;

8. Скільки розв‘язків мають такі конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) ?

9. Розв‘язати двочленні конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) ;

є) ; ж) ;

з) ; к) ;

л) .

10. Розв‘язати конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) .

11. Знайти найменшу натуральне число , яке задовольняє такі конгруенції:

а) ; б) ;

в) ; г) ;

д) ; е) .

Модуль 3

Практичне заняття 5

Арифметичні застосування теорії конгруенцій

Основні теоретичні відомості:

Теорія конгруенцій має ряд арифметичних застосувань. Основними з них є:

1) виведення ознак подільності;

2) обчислення остач при діленні;

3) перевірка результатів арифметичних дій;

4) визначення довжини періоду при перетворенні звичайного дробу в десятковий.

Нехай в -й системі числення число має вигляд

Позначимо через абсолютно найменші лишки числа за модулем , тобто , і . Тоді , де (ознака подільності Паскаля).

З конгруенції випливає, що при діленні на т числа і дають однакові остачі. Зокрема, число ділиться на тоді і тільки тоді, коли на ділиться . Покладаючи , , дістаємо конкретні ознаки подільності. З метою обчислення остач від ділення, крім ознаки Паскаля, використовують також теореми Ейлера і Ферма, властивості індексів тощо.

Якщо

(1)

де — многочлен від цілих чисел з цілими коефіцієнтами, то виконується конгруенція

(2)

де —будь-яке натуральне число, — остача від ділення на , . Конгруенція (2) є умова, необхідна для рівності (1), але не достатня. Інакше кажучи, якщо (2) не виконується, то не виконується й (1); якщо (2) виконується, наприклад, для або , то напевно помилки в обчисленнях (1) не виявлено. Так, виконуючи перевірку для , помилку не виявили, оскільки: 1) не було взято до уваги нуль у доданку або множнику; 2) в результаті цифри записані не в тому порядку; 3) неповні добутки перебувають не на своїх місцях; 4) взагалі, помилка становить число, кратне 9. Під час складних обчислень доцільно робити дві перевірки: одну за модулем 9, а другу — за модулем 11.

Нескоротний дріб виду 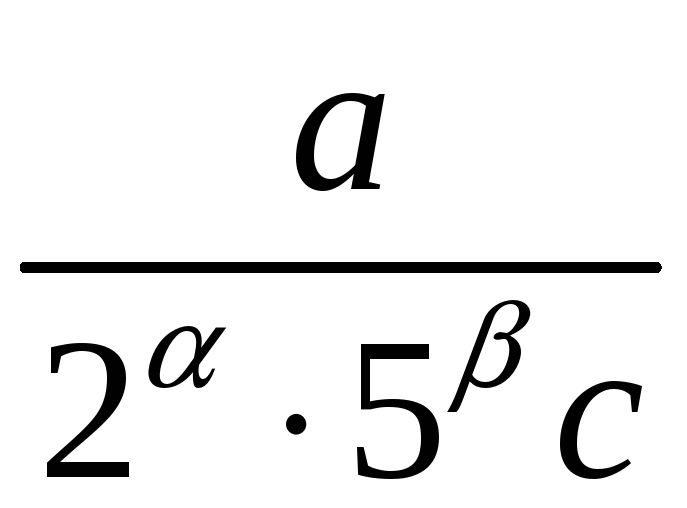, де , і , у скінчений

десятковий дріб не перетворюється.

Якщо — нескоротний дріб і , то цей дріб перетворюється у чистий періодичний десятковий дріб. При цьому число цифр у періоді дорівнює порядку числа 10 за модулем .

Якщо — нескоротний дріб і , де , то цей дріб перетворюється в мішаний періодичний десятковий дріб. При цьому число цифр у періоді дорівнює , де — більше з чисел і ; число цифр у періоді дорівнює порядку числа 10 за модулем .

Задачі рекомендовані для розв‘язання в аудиторії

1. Знайти довжину періоду при перетворенні у десятковий дріб нескоротного звичайного дробу із знаменником: а) 37; б) 59; в) 73.

2. Знайти число цифр до періоду і довжину періоду при перетворенні звичайних дробів у десяткові:

а) ; б) ; в) ; г) .

3. Знайти дві останні цифри числа: а) ; б) , в).

4. Знайти остачу від ділення:

а) на 12; б) на 41.

5. Знайти три останні цифри числа .

6. На основі ознаки подільності на 7, 11 і 13 дізнатися, чи діляться числа 769524 і 1353781 на 7, 11 або 13.

7. Перевірити правильність виконання арифметичних дій числами 9 і 11:

а) ; б) .

Задачі рекомендовані для розв‘язання дома

1. За допомогою таблиць індексів визначити кількість цифр у періоді розкладу дробів 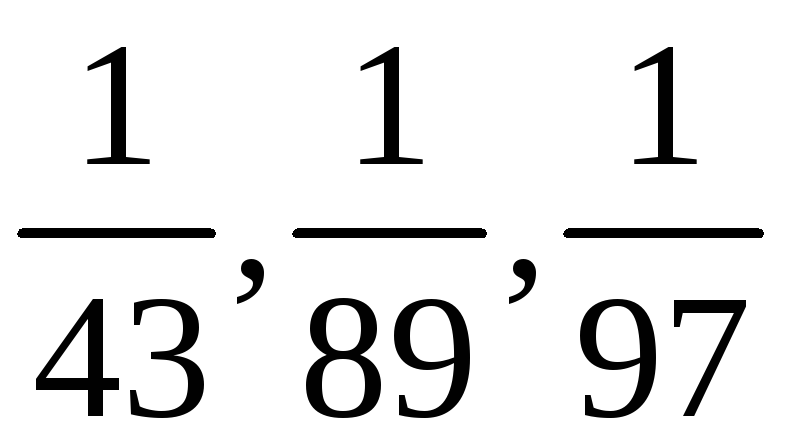у нескінченний десятковий дріб.

2. Знайти остачу від ділення: а) на 21;

б) на 25; в) на 57;

г) на 243.

3. Перевірити правильність результату обчислень числом 9.

а) ;

б) .

4. Перевірити правильність результату обчислень числом 11:

а) ;

б) .

5. Перевірити правильність виконання арифметичних дій числами 9 і 11:

а) ; б) .

Модуль 4

Практичні заняття 1,2

Многочлени над полем . Дії над многочленами. Подільність

многочленів. Найбільший спільний дільник та

його лінійне зображення. Найменше спільне кратне.

Розклад многочлена на незвідні множники.

Основні теоретичні відомості

Нехай - довільна область цілісності з одиницею і - її підкільце з одиницею.

Елемент називається алгебраїчним над кільцем , якщо в існують такі елементи які не дорівнюють , що

Елемент, який не є алгебраїчним над , називається трансцендентним над .

Мінімальне розширення кільця , яке містить трансцендентний над елемент , називається простим трансцендентним розширенням кільця , або кільцем многочленів від однієї змінної над , і позначається через Елементи цього кільця називають многочленами від над і позначають символами і так далі. Нуль кільця називають нульовим многочленом або нуль-многочленом.

Будь-який ненульовий многочлен над кільцем можна єдиним чином подати у вигляді

, (1)

де

Вираз (1) називають канонічною формою ненульового многочлена . Канонічною формою нуль-многочлена вважатимемо .

Доданок канонічної форми (1) ненульового многочлена називається -м членом, м коефіцієнтом, називається також вільним членом многочлена . Член -го (найбільшого) степеня називається старшим членом, його коефіцієнт -

старшим коефіцієнтом, а його степінь – степенем многочлена і позначають

Нуль-многочлену не приписують ніякого степеня.

Два многочлени з кільця дорівнюють один одному тоді і тільки тоді, коли вони мають однакові степені і попарно рівні відповідні коефіцієнти (алгебраїчна рівність многочленів).

Кільце многочленів є областю цілісності.

Степінь суми двох многочленів (з яких хоча б один є ненульовим) не перевищує більшого з степенів цих многочленів. Степінь добутку двох многочленів (відмінних від нуль-многочлена) дорівнює сумі степенів цих многочленів.

Якщо многочлен з кільця має канонічну форму (1) і , то елемент

кільця називають значенням многочлена при і позначають через .

Кожен многочлен з кільця визначає відображення таке, що

Якщо область цілісності має характеристику , то многочлени дорівнюють один одному тоді і тільки тоді, коли рівні функції та , які вони визначають (функціональна рівність многочленів).

Алгебраїчне і функціональне тлумачення многочленів рівносильні над областю цілісності характеристики .

Нехай деяке поле. Многочлен ділиться на (записують ), якщо існує многочлен такий, що

Відношення подільності многочленів над полем має такі властивості:

.

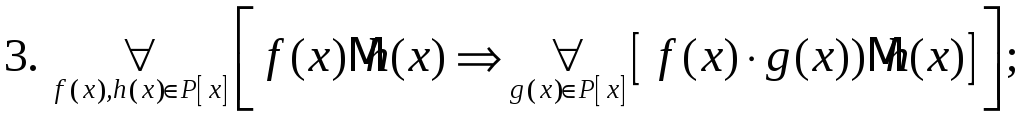
Говорять, що многочлен ділиться з остачею на многочлен з кільця , якщо в існують такі многочлени що:

При цьому називають діленим, - дільником, - часткою, - остачею.

Довільний многочлен з кільця ділиться з остачею на будь-який ненульовий многочлен з цього кільця, причому частка і остача визначаються однозначно.

Кільце многочленів над довільним полем є кільцем головних ідеалів. Кільце многочленів над полем є евклідовим.

Для знаходження частки і остачі від ділення многочлена

на

над полем застосовують різні методи. Зокрема, метод ділення кутом, метод невизначених коефіцієнтів та за допомогою табличних схем.

Розглянемо одну з можливих табличних схем, яка має іноді переваги перед рештою методів. Нехай Якщо

та

то схема має вигляд (таблиця 1).

Таблиця 1

				…			…
				…
				…
. . .
							…
				…			…

У таблиці є стовпці і рядки. Через позначено суму елементів -го стовпця, які стоять між першим та -м рядками. Через позначено суму елементів відповідного стовпця, які стоять між першим і останнім рядками. Таблиця заповнюється так:

1) знаходять і записують його в останній рядок другого стовпця;

2) число множать на коефіцієнти дільника і послідовно записують у другий рядок зліва направо (при цьому кілька останніх клітин можуть бути порожніми);

3) обчислюють різницю і записують її у клітинці на перетині третього рядка і третього стовпця;

4) знаходять число 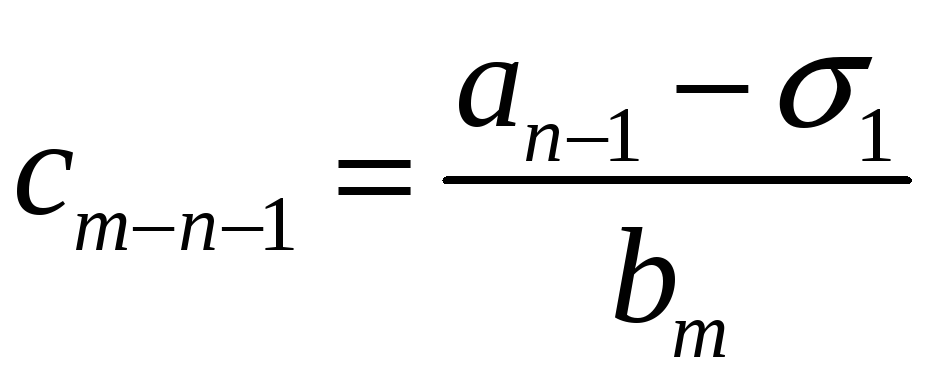і записують його в третій клітинці останнього рядка;

5) за аналогією з 2) заповнюють третій рядок (при цьому порожньою буде клітинка з другого стовпця).

Цей процес продовжують доти, поки не буде обчислено вільний член частки. Після цього знаходять коефіцієнти остачі як різниці між числом, що стоїть у першому та останніх заповнених рядках відповідного стовпця.

Ділення многочлена на значно спрощується, якщо многочлен є двочленом виду Справді, вона має вигляд таблиці 2. З другого по передостанній рядок цієї таблиці в кожному стовпці міститься не більш як одне число, відмінне від нуля. Наприклад, з другого по -й стовпець – це

Таблиця 2

				…			…			…
. . .
										…
				…			…			…

У наступних стовпцях: , 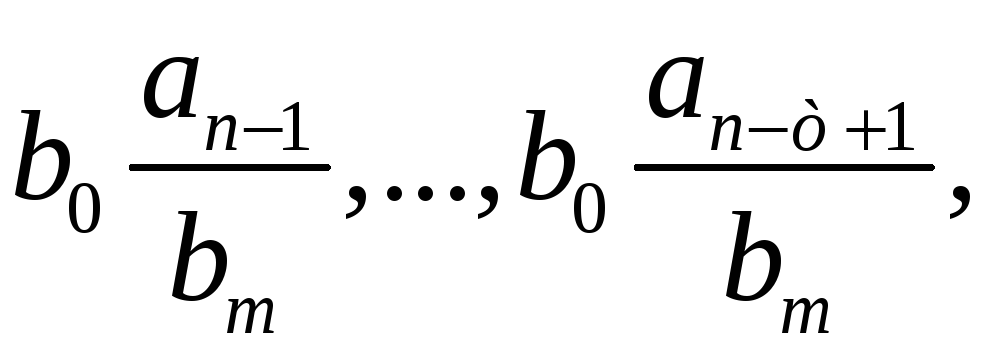тобто добутки вільного члена дільника на коефіцієнти частки і так далі. Це означає, що в таблиці можна обмежитися тільки трьома рядками і заповнювати її в такій послідовності:

1) спочатку розіб’ємо коефіцієнти многочлена у групи по членів зліва направо (в останній групі може бути менше ніж членів);

2) коефіцієнти записують у першому стовпці в першому і другому рядках;

3) кожен ряд певної групи ділять на старший член дільника і записують у третій рядок під ним; у другому рядку з другої по -у клітину можна не вписувати чисел;

4) вільний член послідовно множать на знайдені коефіцієнти частки і вписують у другий рядок, починаючи з -ї клітини;

5) знаходять наступні коефіцієнти частки, і процес продовжують доти, поки не заповнять останню клітину таблиці в третьому рядку.

Якщо двочлен має вигляд то при обчисленні коефіцієнтів частки за наведеною табличною схемою не треба виконувати ділення чисел, тоді ця схема нагадує схему Горнера. При цьому число 1 можна також не писати в лівому верхньому кутку таблиці.

При діленні многочлена на двочлен описану схему можна спростити. Так, якщо усно обчислювати різницю коефіцієнтів і добутків вільного члена - на знайдений коефіцієнт частки то в таблиці стає зайвим другий рядок. Тоді розглядувана таблична схема відрізняється від схеми Горнера тільки тим, що в першому стовпці міститься число замість .

Нехай - деякий многочлен над полем Для будь-якого елемента з поля остача при діленні многочлена на двочлен дорівнює .

Многочлен ділиться на двочлен тоді і тільки тоді, коли остача дорівнює нулю.

Подамо многочлен з кільця у вигляді

де називається розкладом многочлена за степенями . Коефіцієнти розкладу можна знайти в результаті послідовного ділення на , потім здобутої першої частки на і так далі.

Нехай і - многочлени над полем . Якщо і діляться на многочлен з кільця , то називають їхнім спільним дільником.

Спільний дільник многочленів і , який ділиться на кожний їхній спільний дільник, називають найбільшим спільним дільником многочленів і і позначають

Найбільший спільний дільник заданих многочленів визначається однозначно з точністю до сталого множника.

Для будь-яких двох многочленів і з кільця (з яких хоча б один відмінний від 0) існує найбільший спільний дільник, який дорівнює останній відмінній від нуля остачі в алгоритмі Евкліда.

Найбільший спільний дільник многочленів і з кільця завжди можна подати у вигляді

де - деякі многочлени з кільця .

Многочлени називаються взаємно простими, якщо кожен їхній спільний дільник є многочленом нульового степеня. При цьому пишуть

Многочлени і з кільця є взаємно простими тоді і тільки тоді, коли існують многочлени такі, що

Взаємно прості многочлени мають такі властивості:

Спільним кратним многочленів і з кільця називають многочлен такий, що ділиться на і . Найменшим спільним кратним многочленів і називається таке їхнє спільне кратне, на яке ділиться кожне спільне кратне цих многочленів.

Найменше спільне кратне многочленів і визначається однозначно з точністю до сталого множника і позначається через

Для довільних відмінних від нуля многочленів і з кільця найменше спільне кратне існує в і визначається за формулою

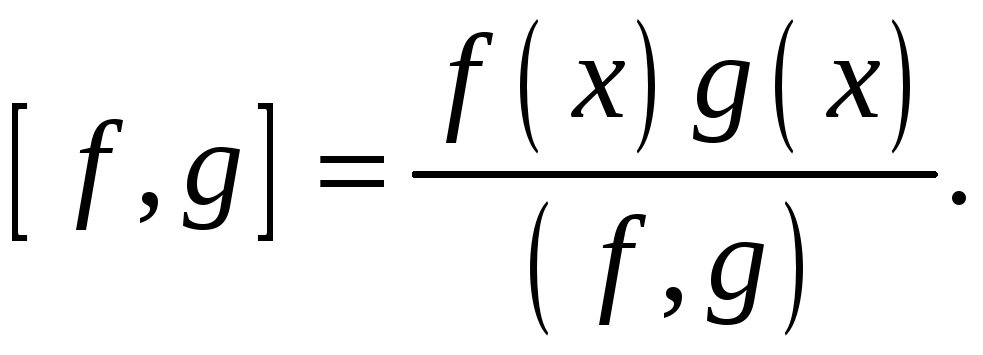
Приклад 1. Знайти числа та , при яких многочлен ділиться на многочлен якщо

Розв’язання. Многочлен має степінь 4; позначимо його степінь – 2. Тому степінь шуканого многочлена (якщо він існує) дорівнює 2. Нехай

і тоді

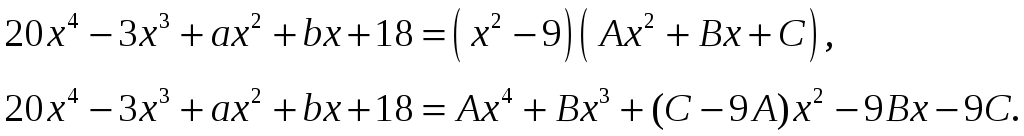
З умови рівності многочленів маємо систему рівнянь:

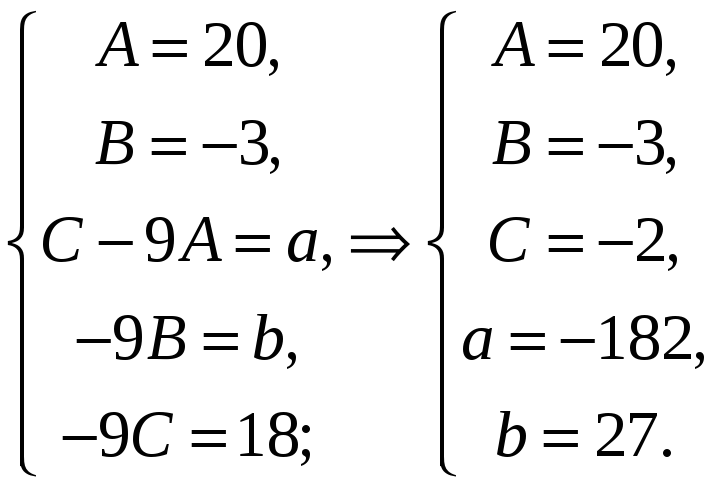
Відповідь: Многочлен ділиться на многочлен при .

Приклад 2. Виконати ділення многочлена

на

в кільці

Розв’язання. Застосуємо табличну схему. В таблиці повинно бути 9 стовпців і 8 рядків. Маємо:

стовпців

рядків

	10	-36	13	38	-6	3	-20	-13
2	10	-20	-15
-4		-16	32	24
3			-4	8	6
				6	-12	-9
					0	0	0
						12	-24	-18
	5	-8	-2-	3	0	6	4	5

Відповідь:

Приклад 3. Виконати ділення многочлена

на в кільці .

Розв‘язання. Маємо: , тоді стовпців

рядків

	4	0	-6	2	0	-4
2	4	-10	2
-5		10	-25	5
1			17
	2	5

Відповідь: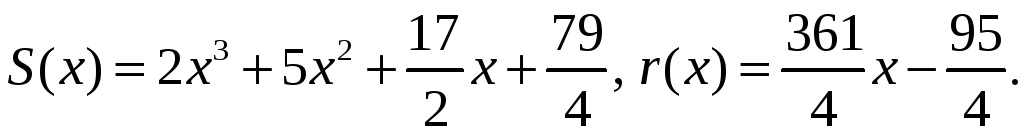

Приклад 4. Знайти найбільший спільний дільник многочленів

і

над полем раціональних чисел.

Розв’язання. Щоб уникнути дробових коефіцієнтів, помножимо попередньо на 3:

Тепер, щоб уникнути дробових коефіцієнтів, помножимо одержану різницю на 3. В даному випадку остача визначиться з точністю до множника нульового степеня.

Таким чином, ми знайшли з точністю до множника нульового степеня остачу від ділення на Тепер потрібно ділити на Ми можемо впевнитися, що ділиться без остачі на Отже, і є найбільший спільний дільник многочленів і

Приклад 5. Визначити так, щоб многочлен ділився на

Розв’язання.

			0	…	0	1
1				…
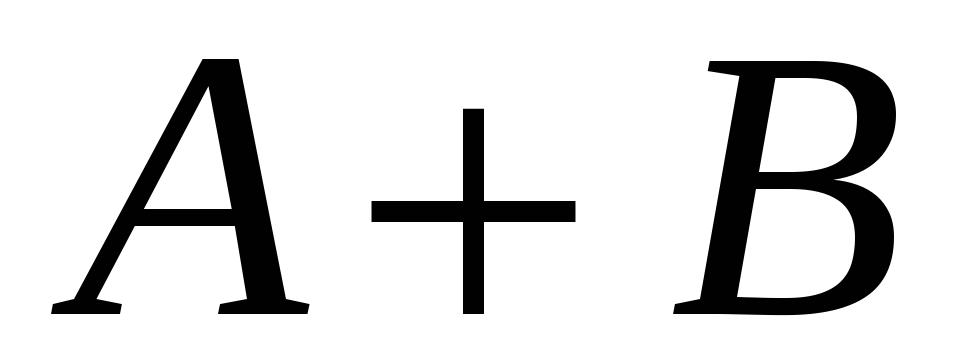
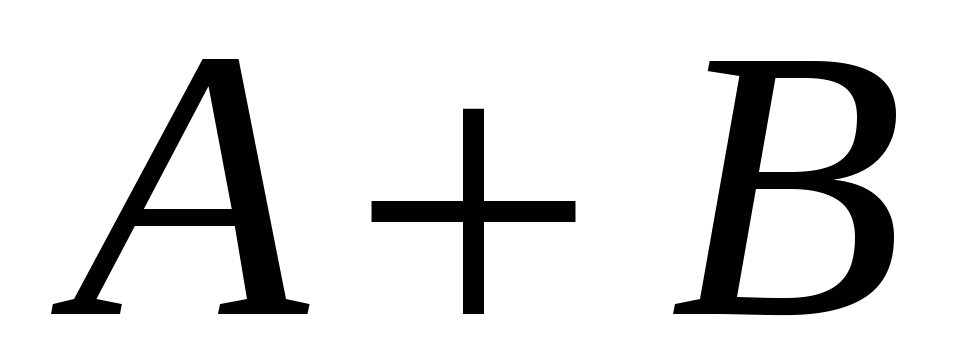
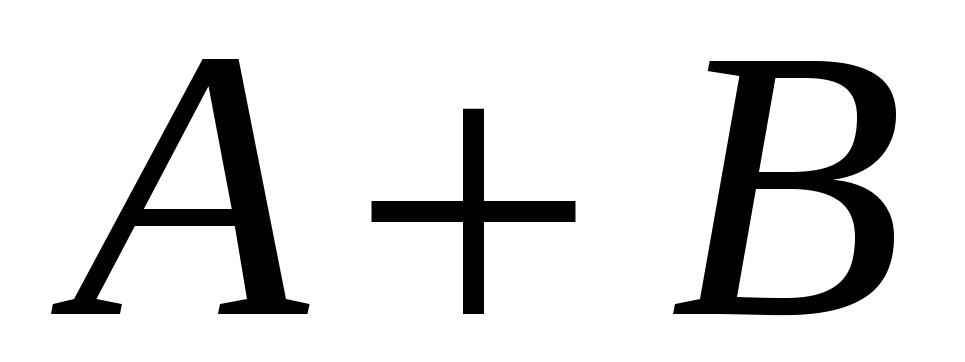
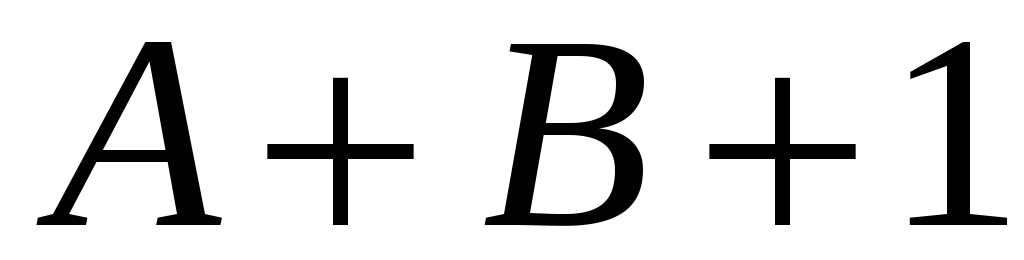
1				…

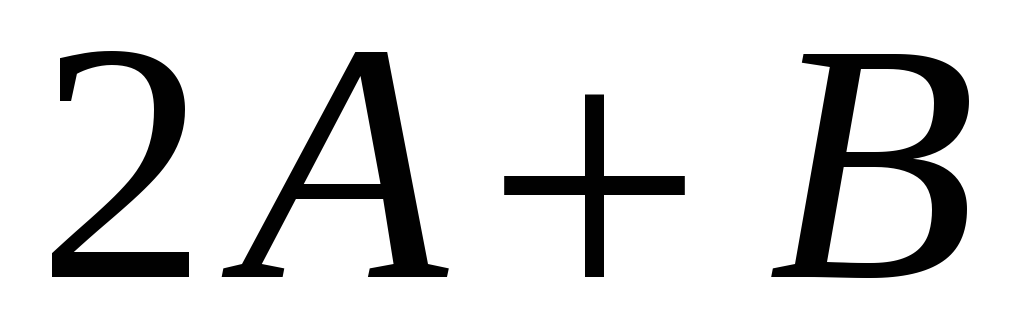
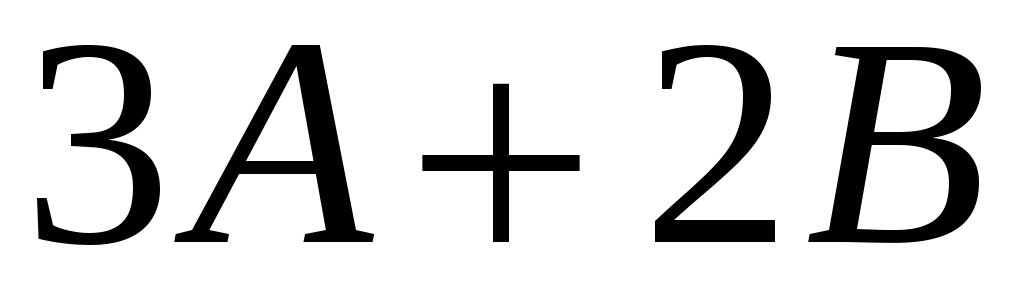
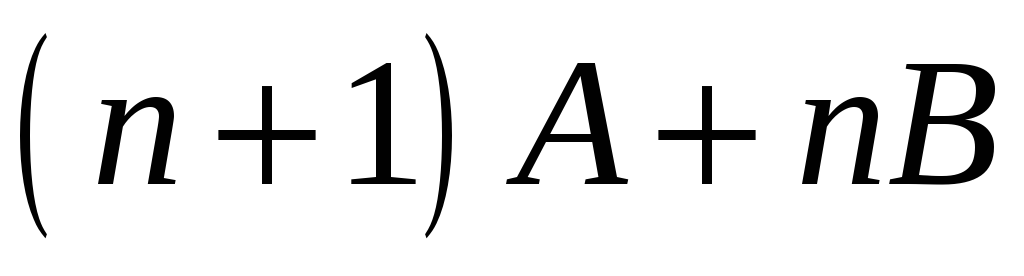
Щоб ділився на потрібно, щоб остачі і дорівнювали нулю. З цієї умови і знаходимо :

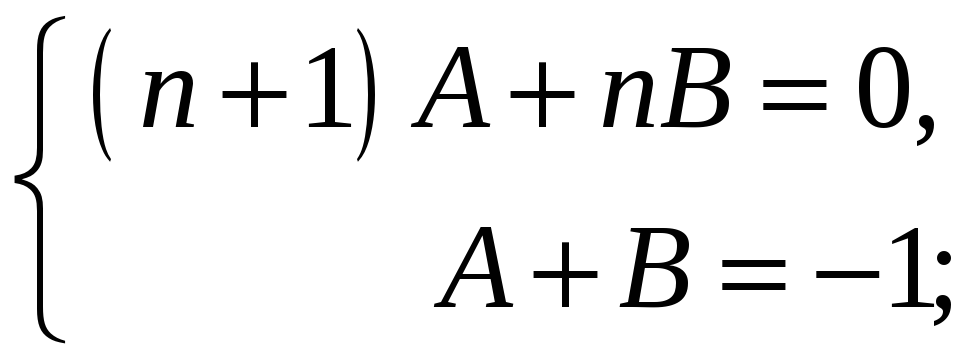
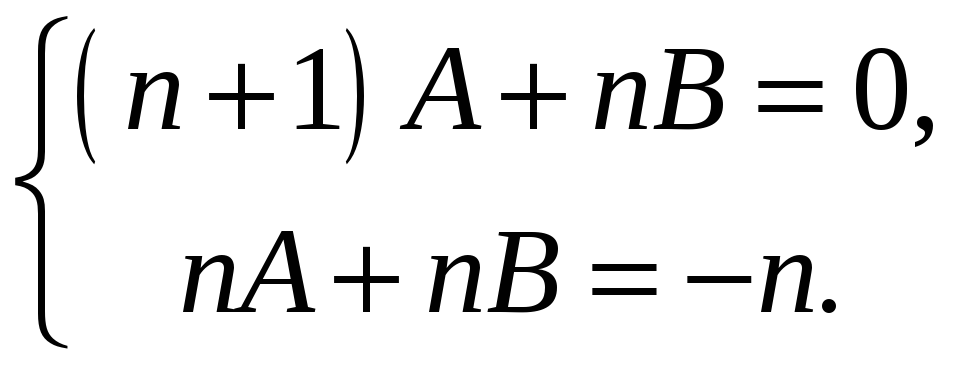
Звідси

Такими будуть наприклад, многочлени:

для

для і так далі.

[Костарчук В. Н. Высшая алгебра Часть ІІ. Алгебра многочленов.]

Приклад 6. При яких значеннях многочлен ділиться без остачі на

Розв’язання. За теоремою Безу тобто

Відповідь:

Приклад 7. Знайти найбільший спільний дільник многочленів та визначити многочлени такі, щоб виконувалась рівність: якщо:

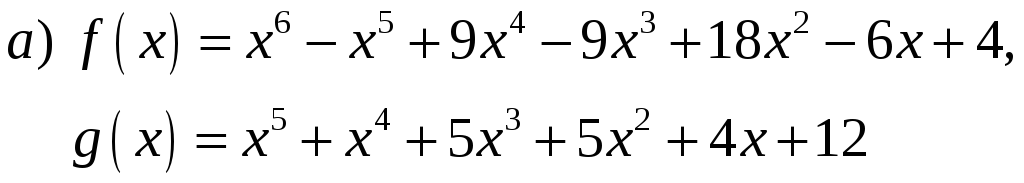
Розв‘язання. І крок

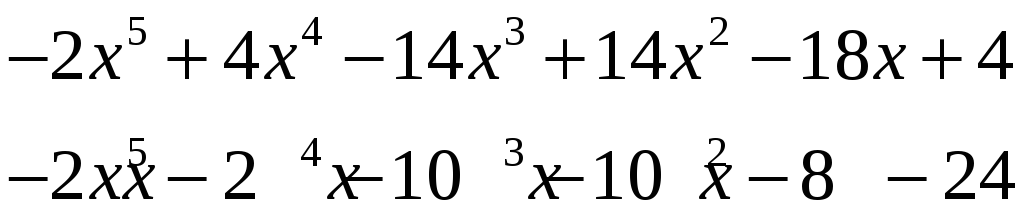
Таким чином

ІІ крок. Поділимо на

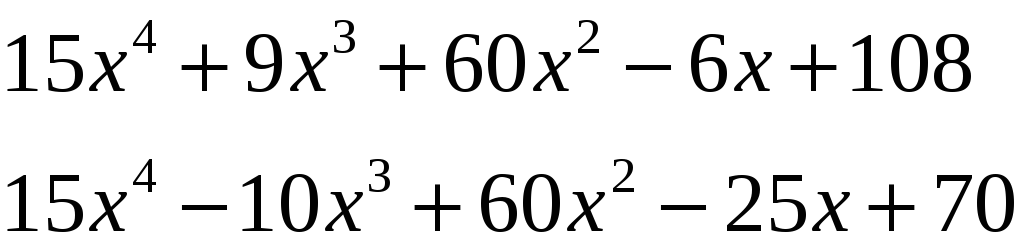
ІІІ крок. Поділимо на

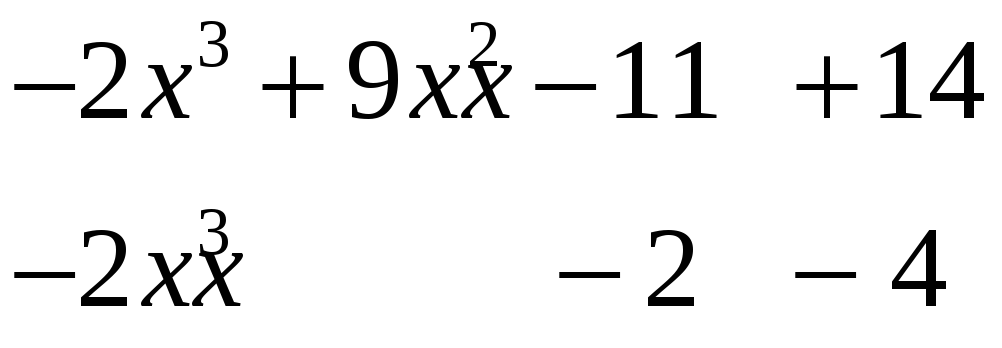
ІV крок. Поділимо на

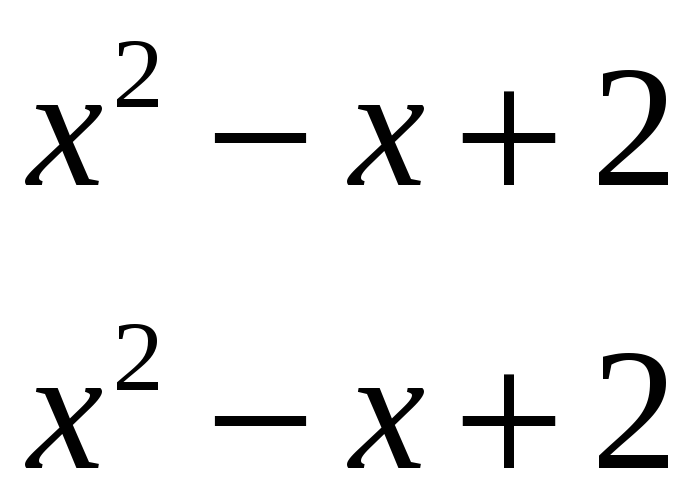
Так як то передостання остача в алгоритмі Евкліда буде найбільшим спільним дільником многочленів .

Із (3) знаходимо

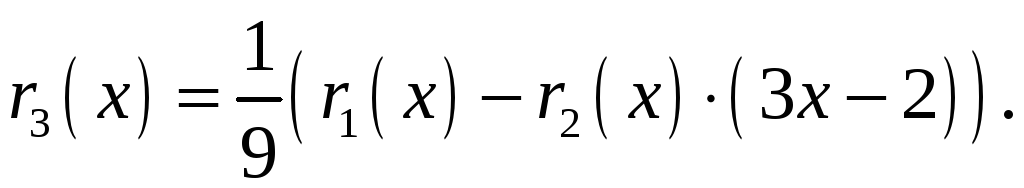
Із (2) виразимо

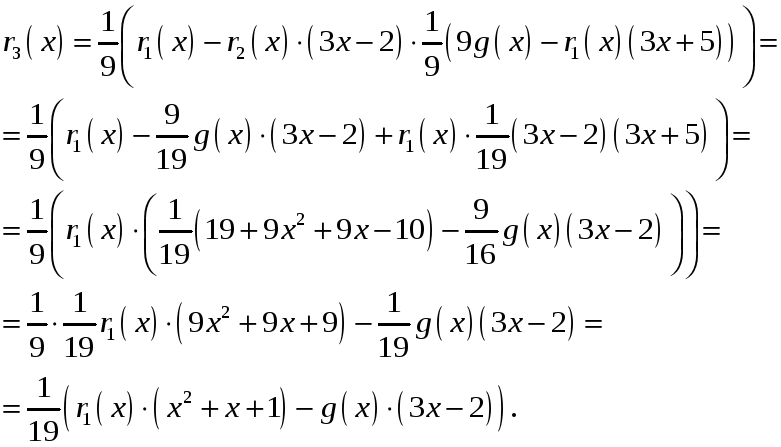
Із (1) виразимо через

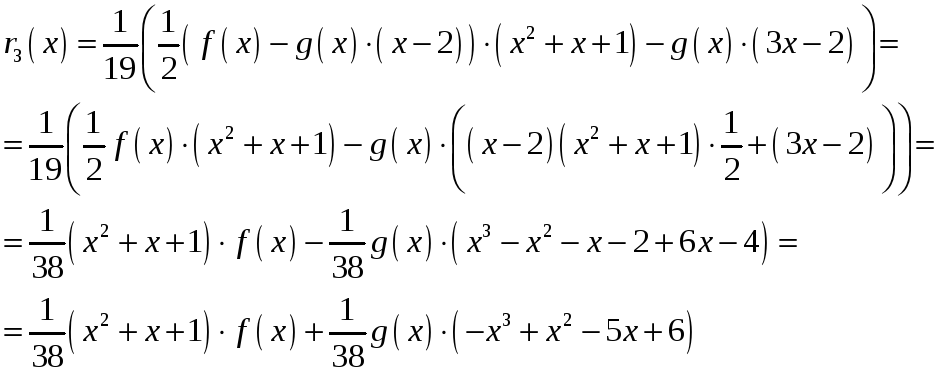
Відповідь:

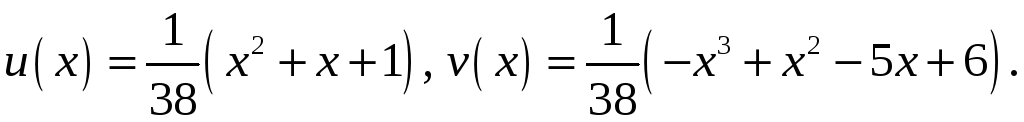
Приклад 8. Розділити многочлен на двочлен

Розв’язання. Виконаємо ділення многочлена на двочлен за схемою Горнера:

	1	2	-16	-2	15
2	1	4	-8	-18	-21

Отже, частка дорівнює а остача

Приклад 9. Розкласти многочлен за степенями двочлена

Розв’язання. Складемо таблицю:

	1	-5	3	-2
2	1	-3	-3	-8
2	1	-1	-5
2	1	1
2	1

У першому рядку цієї таблиці стоять коефіцієнти даного многочлена ; у другому рядку маємо результат ділення на і остачу у третьому рядку маємо вже результат ділення на і остачу що утворилась при цьому діленні, і так далі.

Отже, виділені у таблиці числа є коефіцієнтами шуканого многочлена:

Приклад 10. Обчислити з точністю до 0,001 значення многочлена при

Розв’язання. Розкладемо даний многочлен за степенями двочлена

	1	0	-2	3
1	1	1	-1	2
1	1	2	1
4	1	3
1	1

Якщо то

Відповідь: 1,997027.

Приклад 11. Знайти такі пари многочленів в кільці що де

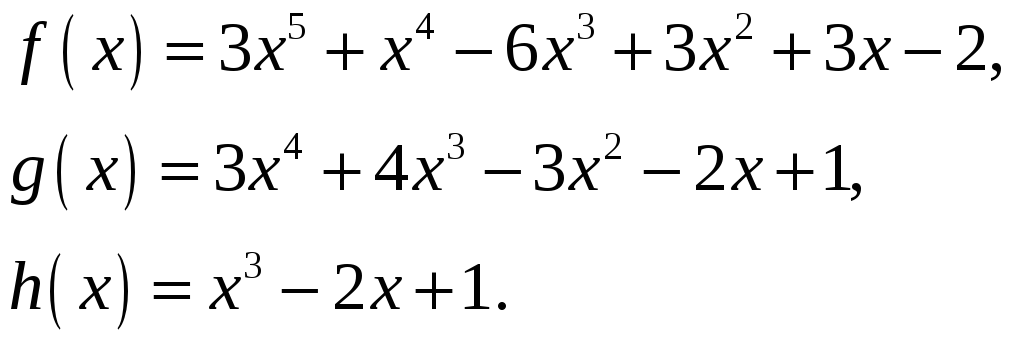
Розв’язання. В кільці нам необхідно розв’язати рівняння (1) з невідомими . Нехай Якщо існує хоча б один розв’язок то так як Нехай Так як многочлен лінійно зображується через многочлени , тобто то , тобто пара многочленів - розв’язок нашого рівняння (1). Таким чином умова необхідна і достатня для існування розв’язку рівняння (1).

Щоб знайти всі можливі розв’язки (коли ), розділимо обидві частини рівняння (1) на

Одержуємо рівносильне рівняння Зафіксуємо який-небудь розв’язок цього рівняння. Нехай - довільні його розв’язки. Тоді

Так як многочлени не мають спільних множників, то

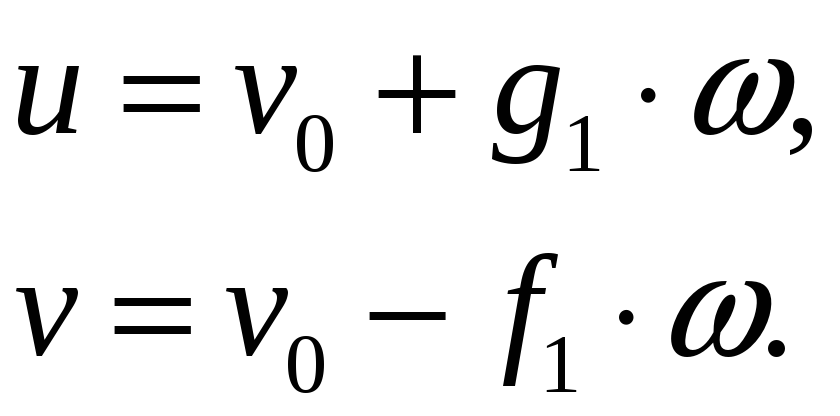(2)

Отже, для будь-якого многочлена пара многочленів одержана із формули (2) дає множину розв’язків рівняння (1), коли пробігає множину всіх многочленів.

За алгоритмом Евкліда знайдемо

Перевіримо подільність на .

Знайдемо лінійне зображення

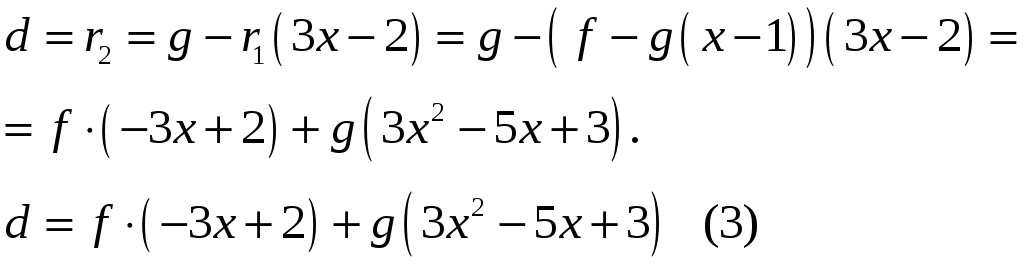
Помножимо обидві частини рівності (3) на

Одержимо

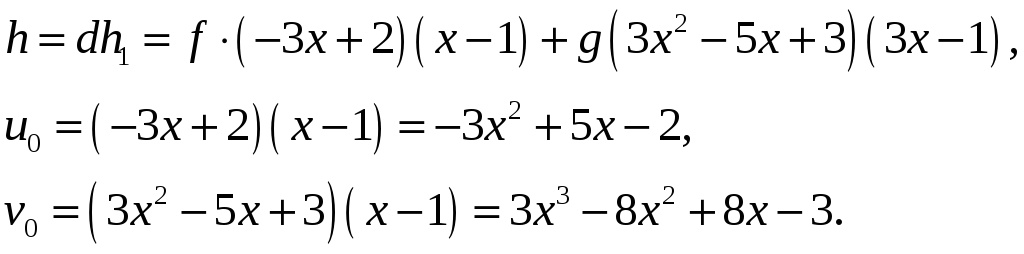
Щоб одержати множину всіх розв’язків, необхідно обчислити

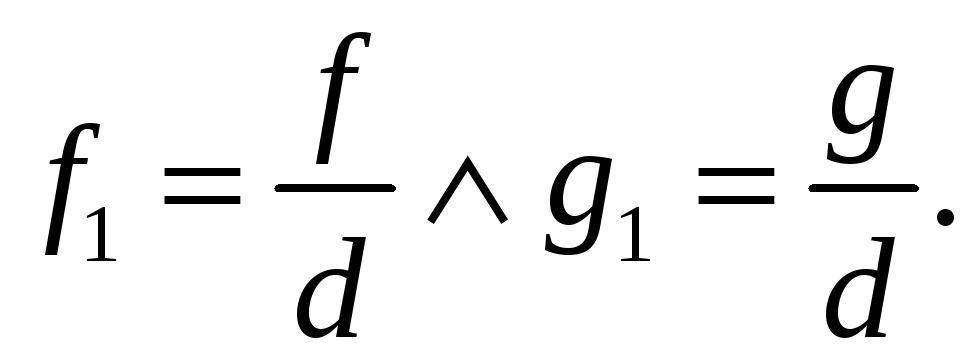
Виконаємо ділення

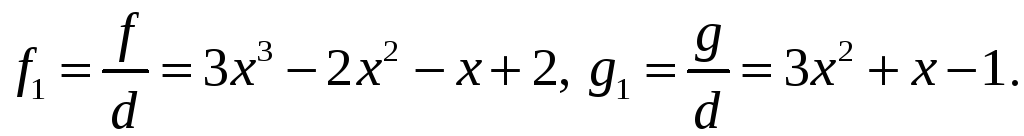
Отже, шукані розв’язки матимуть вигляд:

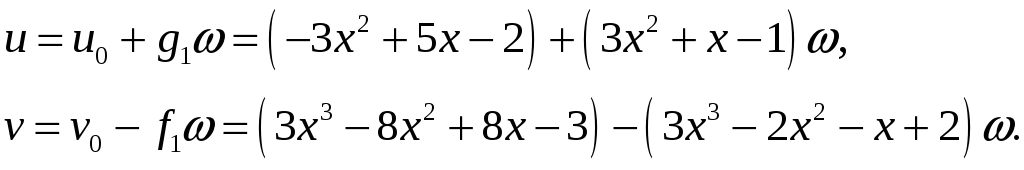
Задачі для розв’язування в аудиторії

І рівень

Виконайте ділення многочлена на многочлен (трьома способами)

,

,

,

,

,

,

,

,

,

,

ІІ. При яких значеннях многочлен ділиться без остачі на , а при діленні на дає остачу, яка дорівнює

ІІІ. При яких значеннях многочлен ділиться без остачі на

ІV. Знайти найбільший спільний дільник та найменше спільне кратне многочленів

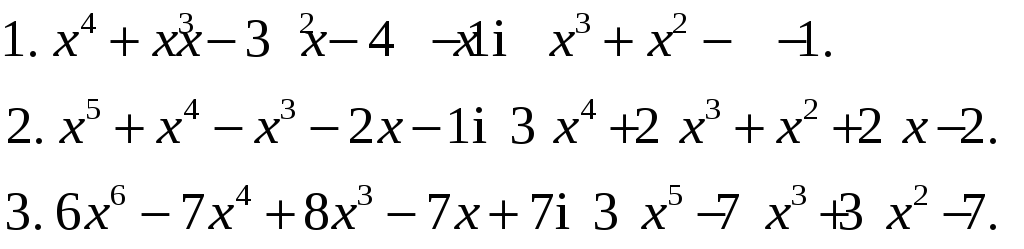
ІІ рівень

1. Розкласти многочлен за степенями :

а) ;

б) ;

в)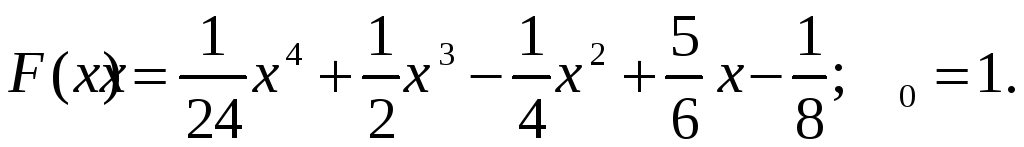

2. Знайти найбільший спільний дільник та найменше спільне кратне многочленів

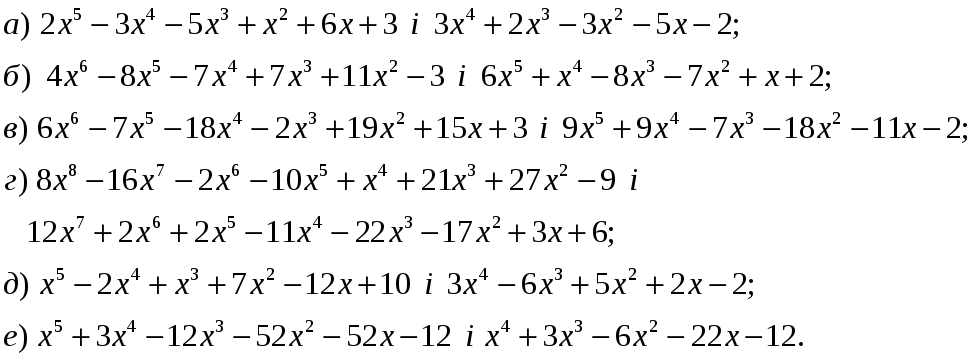3. Для многочленів i визначити многочлени i так, щоб де

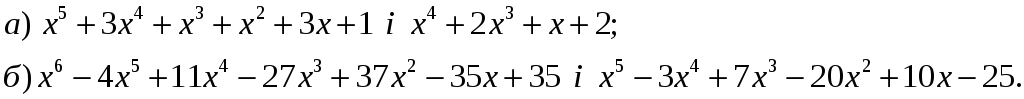ІІІ рівень

Визначення параметрів:

1. Визначити параметр так, щоб многочлен мав коренем не нижче другої кратності.

2. Визначити коефіцієнти так, щоб многочлен мав число коренем не нижче третьої кратності.

3. При якій умові многочлен має відмінний від нуля корінь кратності ?

4. Для многочленів i визначити многочлени i так, щоб

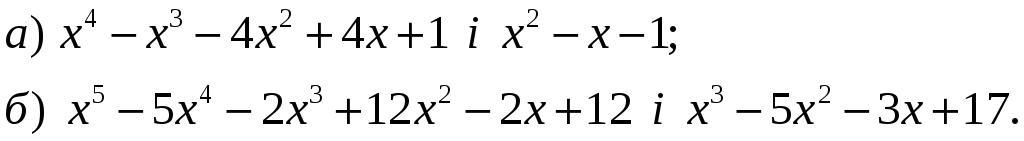
5. Знайти значення і , при яких многочлен ділиться на многочлен

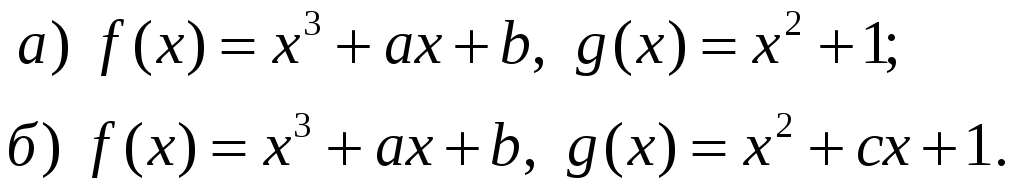
Задачі для розв’язання дома

І рівень

1. Виконайте ділення многочлена на многочлен (трьома способами)

,

,

,

,

,

,

,

,

,

,

2. Знайти найбільший спільний дільник та найменше спільне кратне многочленів

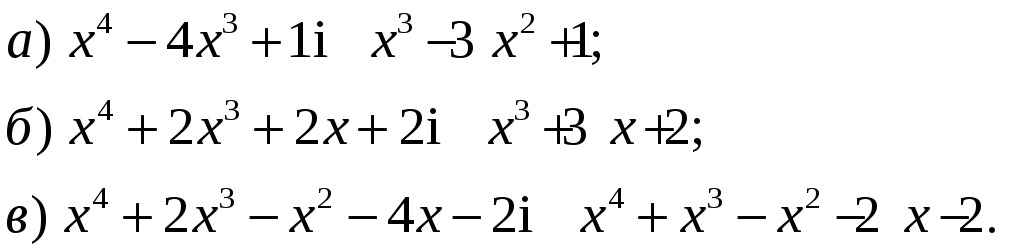
3. Знайти найбільший спільний дільник многочленів та визначити многочлени такі, щоб виконувалась рівність:

якщо:

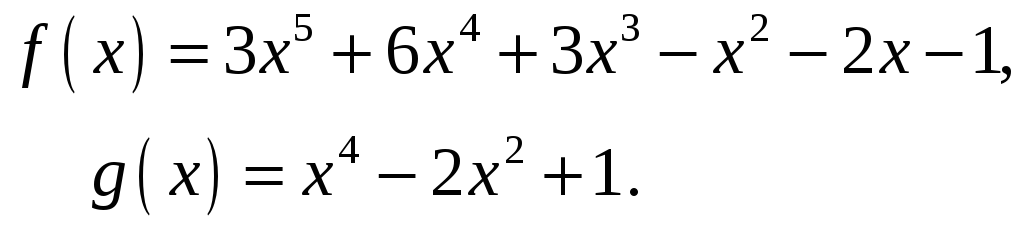
4. При яких значеннях многочлен при діленні на дає остачу а на ділиться без остачі?

5. При яких значеннях многочлен ділиться без остачі на а при діленні на дає остачу

ІІ рівень

1. Розкласти многочлен за степенями :

а)

б)

в)

2. Знайти найбільший спільний дільник і найменше спільне кратне многочленів:

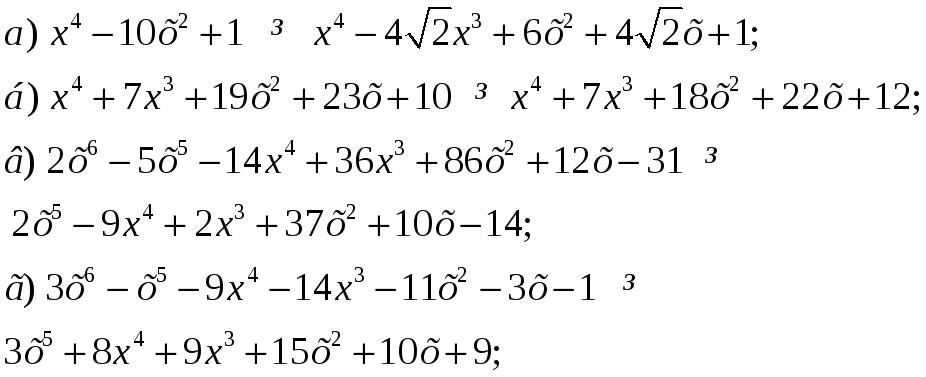
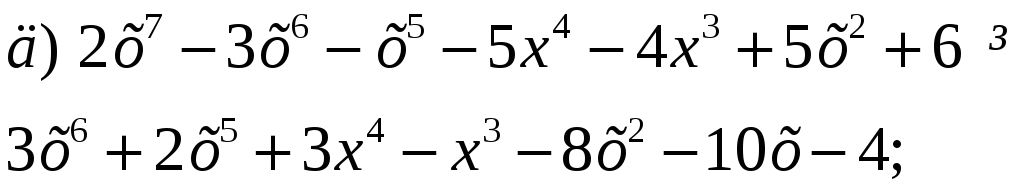
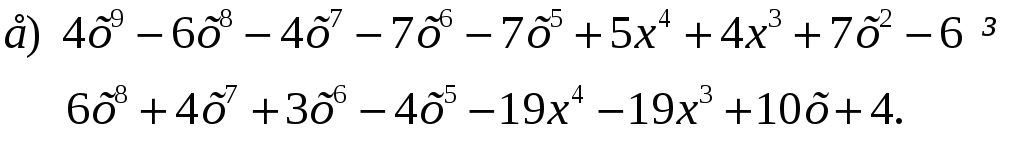
3. Знайти найбільший спільний дільник многочленів та визначити многочлени такі, щоб виконувалась рівність:

якщо:

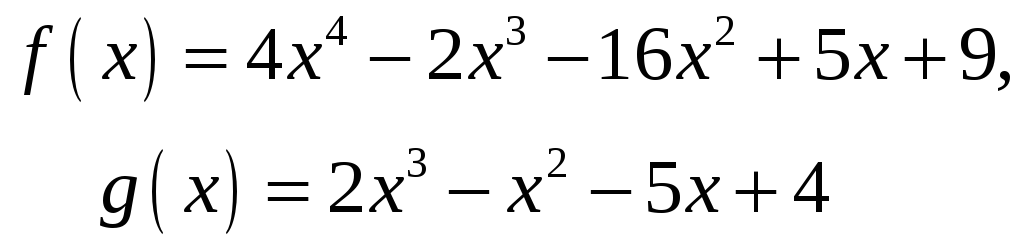
4. Для многочленів i визначити многочлени i так, щоб де

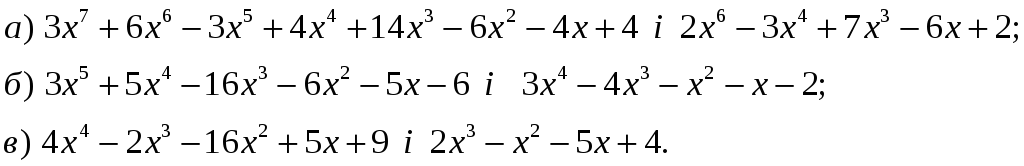
ІІІ рівень

1. Визначити так, щоб многочлен ділився на

2. Визначити параметр так, щоб було коренем кратності многочлена

3. Визначте параметр так, щоб було коренем кратності многочлена

4. Для многочленів i визначити многочлени i так, щоб

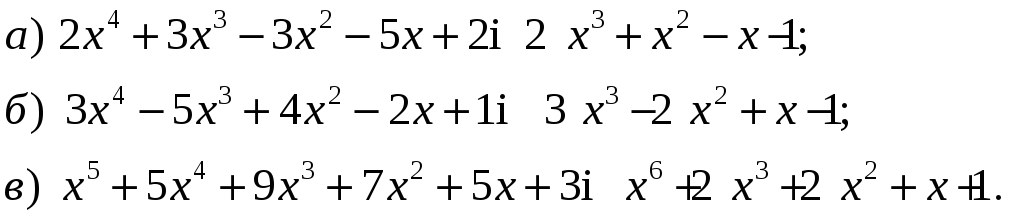
5. Знайти найбільший спільний дільник многочленів та визначити многочлени такі, щоб виконувалась рівність:

якщо:

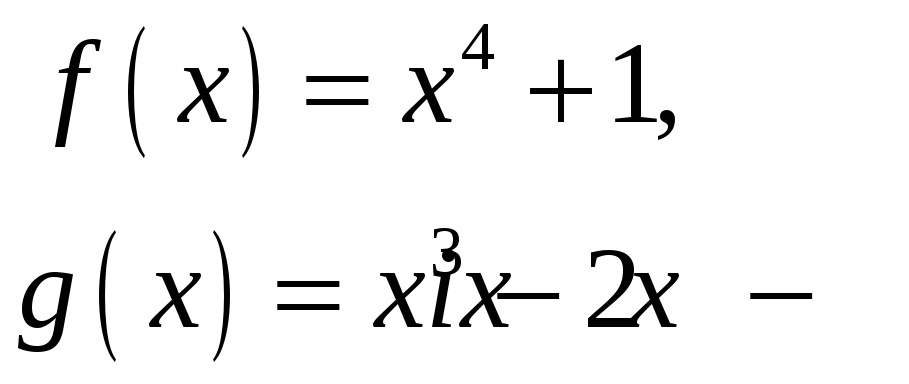
6. Знайти значення і , при яких многочлен ділиться на многочлен

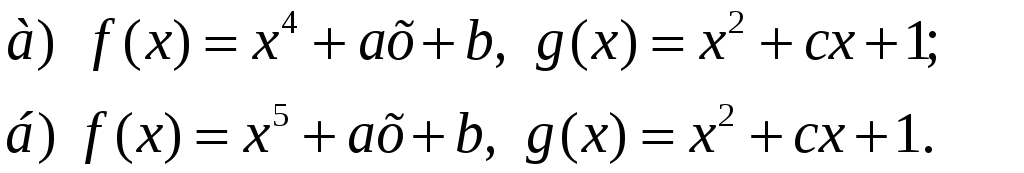
7. Знайти такі пари многочленів в кільці що де

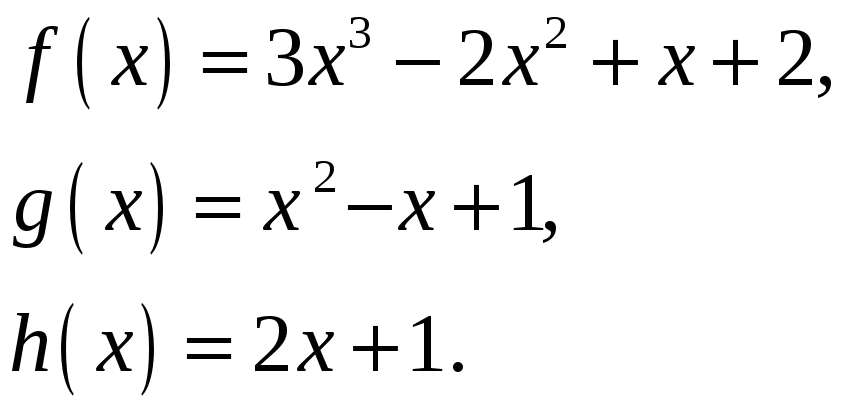
Задачі для самостійного розв’язування

1. Розкласти многочлен за степенями

2. Розкласти многочлен за степенями

3. Розкласти многочлен за степенями

.

4. Розкласти многочлен за степенями

.

5. Знайти числа при яких многочлен

ділиться на двочлен

6. При яких значеннях многочлен буде повним квадратом многочлена

7. а)

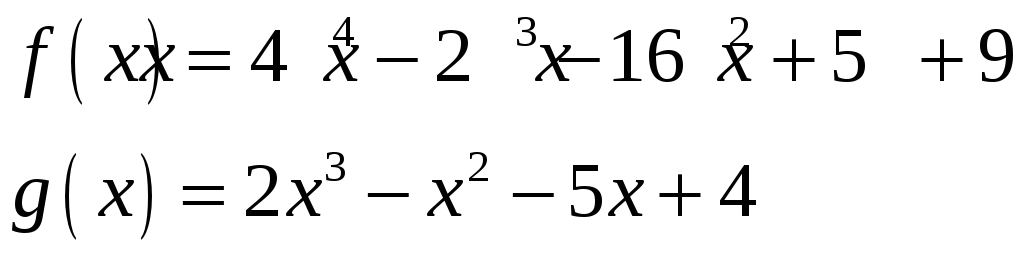
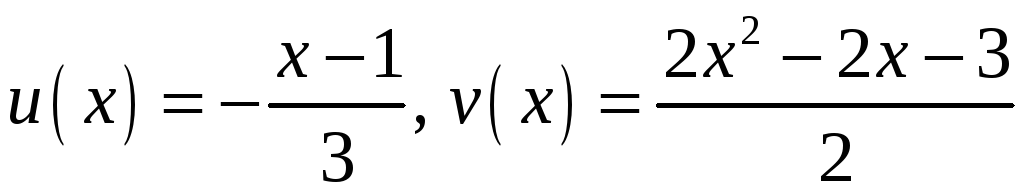
б)

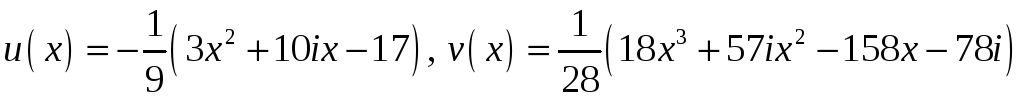
8. При яких значеннях многочлен буде повним квадратом квадратного тричлена

9. При яких значеннях многочлен буде повним квадратом многочлена

10. Виконати ділення многочлена на в кільці .

11. Виконати ділення многочлена на в кільці

Модуль 4

Практичне заняття 3.

Відокремлення кратних множників многочлена