
- •§1 Рівняння прямої лінії у просторі
- •§2 Пряма і площина у просторі
- •Розділ 1. Теоретичні відомості до теми «Пряма у просторі»
- •§1 Рівняння прямої лінії у просторі.
- •1.1 Канонічні рівняння прямої у просторі
- •1.2 Рівняння прямої, яка проходить через дві точки
- •1.3 Параметричні рівняння прямої
- •1.4 Рівняння прямої як лінії перетину двох площин
- •1.5 Взаємне розташування прямих
- •1.6 Кут між двома прямими у просторі
- •§2 Пряма і площина у просторі
- •2.1 Умова належності двох прямих площині
- •2.2 Кут між прямою і площиною
- •2.3 Взаємне розташування прямої і площини
- •Питання для самоперевірки
- •Розділ 2. Аудиторні практичні заняття
- •3. Рівняння прямої як лінії перетину двох площин:
- •Розділ 3.Індивідуальні домашні завдання
Міністерство освіти і науки України
Миколаївський державний університет
імені В.О.Сухомлинського
Методичні рекомендації і дидактичні матеріали для студентів
фізико-математичних факультетів вищих навчальних закладів
Векторна алгебра та аналітична
геометрія.
Пряма у просторі
Розділ 1. Теоретичні відомості до теми «Пряма у просторі»
§1 Рівняння прямої лінії у просторі
1.1 Канонічні рівняння прямої у просторі………………………….3
1.2 Рівняння прямої, яка проходить через дві точки………………3
1.3 Параметричні рівняння прямої………………………………….4
1.4 Рівняння прямої як лінії перетину двох площин………………4
1.5 Взаємне розташування прямих………………………………….5
1.6 Кут між двома прямими у просторі……………………………..6
§2 Пряма і площина у просторі
2.1 Умова належності двох прямих площині………………………7
2.2 Кут між прямою і площиною……………………………………8
2.3 Взаємне розташування прямої і площини……………………...9
Питання для самоперевірки………………………………………….10
Розділ 2. Аудиторні практичні заняття…………………………………...11
Розділ 3. Індивідуальні домашні завдання……………………………….23
Література
Розділ 1. Теоретичні відомості до теми «Пряма у просторі»
§1 Рівняння прямої лінії у просторі.
1.1 Канонічні рівняння прямої у просторі
Пряму
![]() у просторі можна визначити точкою
у просторі можна визначити точкою
![]() ,
яка належить цій прямій, і напрямним
вектором
,
яка належить цій прямій, і напрямним
вектором
![]() цієї прямої (рис.1.1).
цієї прямої (рис.1.1).
Візьмемо
на прямій
![]() плинну точку
плинну точку
![]() і побудуємо вектор
і побудуємо вектор
![]() ,
який матиме проекції
,
який матиме проекції
![]() .
Вектори
.
Вектори
![]() і
і
![]() — колінеарні, а тому їх відповідні
проекції пропорційні. Отже, маємо:
— колінеарні, а тому їх відповідні
проекції пропорційні. Отже, маємо:
![]() (1)
(1)
Рівняння (1) є канонічним рівнянням прямої у просторі.
Зауваження. Коли у рівнянні (1) один із знаменників дорівнює нулю, то відповідний чисельник теж дорівнює нулю.
Приклад.
Визначити положення прямої![]() .
.
Розв’язання.
Дану пряму задано канонічними рівняннями
(1).Оскільки
![]() ,
то
,
то
![]() .
Отже, пряма перетинає вісь
.
Отже, пряма перетинає вісь
![]() у точці
у точці
![]() і
перпендикулярна до цієї осі.
і
перпендикулярна до цієї осі.
1.2 Рівняння прямої, яка проходить через дві точки
Пряму
![]() у
просторі можна визначити двома точками
у
просторі можна визначити двома точками
![]() і
і
![]() ,
що належать цій прямій (рис.1.2).
,
що належать цій прямій (рис.1.2).
В ізьмемо
на прямій
ізьмемо
на прямій
![]() плинну
точку
плинну
точку
![]() і
побудуємо вектори
і
побудуємо вектори
![]() ,
,
![]() .
.
Вектори![]() і
і
![]() – колінеарні , а тому їх відповідні
проекції пропорційні.
– колінеарні , а тому їх відповідні
проекції пропорційні.
Отже,
![]() (2)
(2)
Рівняння (2) є рівнянням прямої у просторі , яка проходить через дві точи.
1.3 Параметричні рівняння прямої
Якщо в
рівнянні (1) значення відношень позначити
параметром
![]() :
:
![]()
а потім
розв’язати одержані рівняння відносно
![]() ,
то дістанемо:
,
то дістанемо:
 (3)
(3)
Так
само, як і для прямої на площині, змінна
![]() набуває довільних дійсних значень і
називається параметром. Коли точка
набуває довільних дійсних значень і
називається параметром. Коли точка
![]() рухається по прямій, параметр
рухається по прямій, параметр
![]() змінюється за абсолютною величиною і
знаком.
змінюється за абсолютною величиною і
знаком.
Рівняння (3) називаються параметричними рівняннями прямої.
Параметричні рівняння зручно застосовувати в тих випадках, коли потрібно знати точку перетину прямої і площини.
Приклад.
Дана пряма
![]() і площина
і площина
![]() .
Знайти точку їх перетину.
.
Знайти точку їх перетину.
Розв’язання. Дану пряму задано канонічними рівняннями. Параметричні рівняння прямої, що відповідають даним канонічним, матимуть вигляд:
![]()
Підставивши ці вирази в ліву частину даного рівняння площини, приходимо до одного рівняння з одним невідомим:
![]()
Розв’язавши
це рівняння, знаходимо
![]() ,
а значить, координати шуканої точки
будуть:
,
а значить, координати шуканої точки
будуть:![]()
1.4 Рівняння прямої як лінії перетину двох площин
Пряма
![]() може бути задана як лінія перетину двох
площин (Рис.1.3)
може бути задана як лінія перетину двох
площин (Рис.1.3)
 (4)
(4)
Нормальні
вектори цих площин матимуть координати
![]() .
Напрямний вектор
.
Напрямний вектор
![]() цієї прямої можна обчислити, як векторний
добуток векторів
цієї прямої можна обчислити, як векторний
добуток векторів
![]() і
і
![]() :
:
 (5)
(5)
Для
того, щоб від рівнянь (4) перейти до
канонічних рівнянь прямої (1), необхідні,
крім координат вектора
![]() ,
координати точки
,
координати точки
![]() ,
яка належить цій прямій. Точку
,
яка належить цій прямій. Точку
![]() беруть
як перетин даної прямої з однією із
координатних площин:
беруть
як перетин даної прямої з однією із
координатних площин:
-
якщо з площиною
 ,
то
,
то
 ;
; -
якщо з площиною
 ,
то
,
то
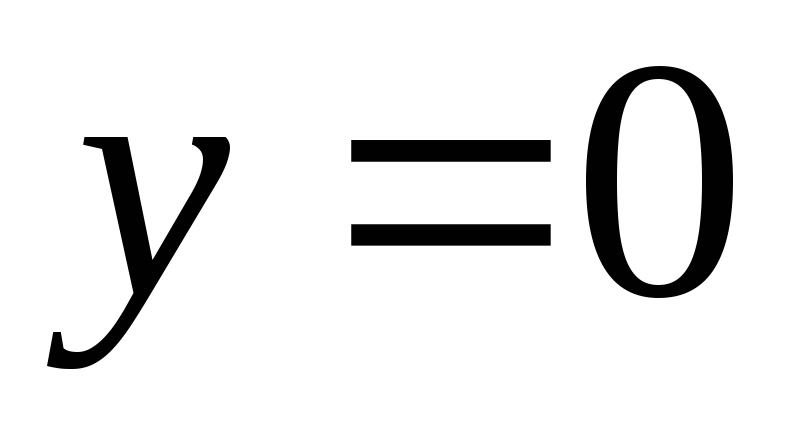 ;
; -
якщо з площиною
 , то
, то
 .
.
У
будь-якому разі з рівнянь (4) дістаємо
систему двох рівнянь із двома невідомими,
розв’язавши яку дістанемо координати
точки
![]() .
.
