План

1. Короткі теоретичні відомості………………………………………….2

2. Питання для самоперевірки……………………………………………8

3. Методичні вказівки до розв’язування задач…………………………..9

4. Задачі до практичних занять………………………………………….15

5. Завдання для самостійної роботи…………………………………….23

6. Відповіді………………………………………………………………..40

7. Література……………………………………………………………...51

Пряма у просторі. Короткі теоретичні відомості. Пряма та її рівняння. Різні способи задання прямої в афінній системі координат.

У просторі пряма може бути задана:

1. Двома різними точками M_l (x_l, y_l, z_l) і M₂ (x₂, y₂, z₂). Тоді її рівняння має вигляд: ;

2. Як лінія перетину двох площин і : , де коефіцієнти при x, y, z не пропорційні. Така пряма l паралельна вектору: .

3. Точкою M₀(x₀, y₀, z₀) і направляючим вектором (α, β, γ), тоді її рівняння мають вигляд – і називаються канонічними рівняннями прямої, де M (x, y, z) – довільна точка прямої.

Якщо одна із координат направляючого вектора, наприклад α = 0, то рівняння можна записати у вигляді: 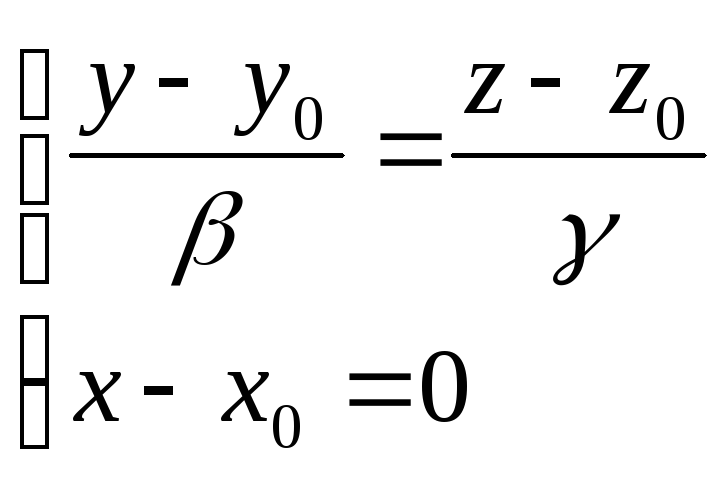. Аналогічно, якщо β = 0 або γ= 0.

Якщо α = β = 0, то рівняння можна записати у вигляді . Аналогічно для а = γ = 0 та β = γ = 0. У всіх цих випадках ми отримали прямі лінії, задані як перетин двох площин, які паралельні до координатних площин.

г) Параметричні рівняння прямої (їх можна одержати з канонічних, позначивши ).

– параметричні рівняння, де t - параметр;

Взаємне розташування двох прямих у просторі.

Нехай задано дві прямі l₁ та l₂, які визначаються відповідно: l₁ – точкою M₁ (x₁, y₁, z₁) і направляючим вектором (α₁, β₁, γ₁) і l₂ – точкою M₂ (x₂, y₂, z₂) і направляючим вектором (α₂, β₂, γ₂). Можливі слідуючи випадки розташування прямих:

1. Мимобіжні: тоді мішаний добуток (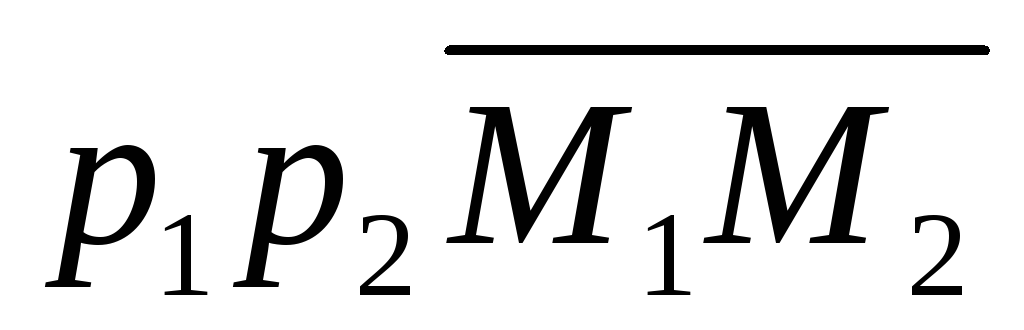) 0 запишемо цю умову в координатному вигляді:

.

2. Співпадають: тоді (у колінеарних векторів відповідні координати пропорційні).

3. Паралельні:

4. Перетинаються: мішаний добуток векторів () = 0 і .

Інакше взаємне розташування двох прямих у просторі можна визначити за допомогою рангів матриць. Розглянемо матриці , та позначимо через R та r ранги цих матриць. Тоді:

1. Прямі l₁ та l₂ мимобіжні тоді і лише тоді, коли R = 3;

2. Прямі l₁ та l₂ перетинаються тоді і лише тоді, коли R = r = 2;

3. Прямі l₁ та l₂ паралельні тоді і лише тоді, коли R = 2, r = 1;

4. Прямі l₁ та l₂ співпадають тоді і лише тоді, коли R = r = 1.

Знаходження відстані від точки до прямої.

Я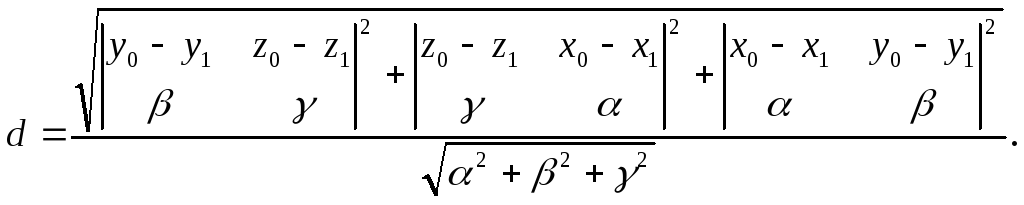 кщо у прямокутній декартовій системі координат пряма l задана точкою M₁(x₁, y₁, z₁) та направляючим вектором (α, β, γ), тоді відстань від точки М₀ (х₀ , у₀ , z₀) до даної прямої знаходиться як висота паралелограма по формулі:

Знаходження відстані між двома мимобіжними прямими.

Якщо у прямокутній декартовій системі координат дано дві мимобіжні прямі рівняннями (l₁): та (l₂): , то відстань d між ними знаходиться за формулою: .

Кут між двома прямими.

Нехай у просторі дві прямі задані їхніми рівняннями відносно де­якої прямокутної системи координат:

, .

Якщо прямі мимобіжні, то кут між ними дорів­нює куту між прямими, що перетинаються і, відповід­но, паралельними кожній із даних мимобіжних прямих. Кут між паралельними прямими вважається рівним 0.

При знаходженні кута між прямими можливі два випадки:

1. Кут  між прямими дорівнює куту між їх направ­ляючими векторами:

 = (). Тоді: cos  = cos () = ,

бо цей кут не перевищує і його косинус невід'ємний.

2. Кут  між прямими є доповнюючим до кута між направляючими векторами. Тоді  = π – ().

< () < π, тому cos () < 0, а

cos  = cos (π – ()) = - cos () = .

В обох випадках cos  = . Отже, cos  = або cos  = – формула косинуса кута між двома прямими.

Якщо прямі l₁ та l₂ взаємно перпендикулярні, то кут  між ними дорівнює 90⁰, a cos 90⁰ = 0. Це буде тоді і тільки тоді, коли у формулі косинуса кута між двома прямими чисельник дорівнює нулю.

Отже, дві прямі l₁ та l₂ , задані канонічними рівняннями будуть взаємно перпендикулярними тоді і тільки тоді, коли викону­ється рівність = 0.