
- •Введение
- •1. Одномерные распределения случайных величин
- •2. Совместное распределение нескольких случайных величин
- •3. Числовые характеристики случайных величин
- •4. Центральная предельная теорема
- •Список литературы
- •Функция распределения нормального закона
- •Содержание
- •Редактор и. Г. Скачек
- •197376, С.-Петербург, ул. Проф. Попова, 5
3. Числовые характеристики случайных величин
▼ Математическим
ожиданием,
или средним значением,
непрерывной случайной величины
X
называется
постоянная, которую обозначают символом
![]() и определяют
равенством
и определяют
равенством
![]()
Замечание. Как и в случае дискретного
распределения, математическое ожидание
для дискретных случайных величин можно
интерпретировать как центр масс.
Действительно, если предположить, что
вдоль вещественной прямой непрерывно
распределена масса с плотностью
распределения
![]() ,
то выражение для математического
ожидания можно интерпретировать как
центр масс. Поэтому точно так же, как и
в случае дискретного распределения,
математическое ожидание можно
рассматривать как центральную точку
случайной величины.
,
то выражение для математического
ожидания можно интерпретировать как
центр масс. Поэтому точно так же, как и
в случае дискретного распределения,
математическое ожидание можно
рассматривать как центральную точку
случайной величины.
Для непрерывных случайных величин математическое ожидание обладает теми же свойствами, что и для дискретных случайных величин. Перечислим их:
1. Математическое
ожидание постоянной равно ей самой
![]() .
.
2. Постоянный
множитель можно выносить за знак
математического ожидания
![]() .
.
3. Математическое
ожидание алгебраической суммы конечного
числа случайных величин равно такой же
сумме их математических ожиданий, т. е.
![]() .
.
4. Математическое
ожидание произведения двух независимых
случайных величин равно произведению
их математических ожиданий, т. е.
![]() .
Данное свойство естественным образом
распространяется на любое число
независимых случайных величин.
.
Данное свойство естественным образом
распространяется на любое число
независимых случайных величин.
Для вычисления
числовых характеристик непрерывной
случайной величины удобно использовать
формулу
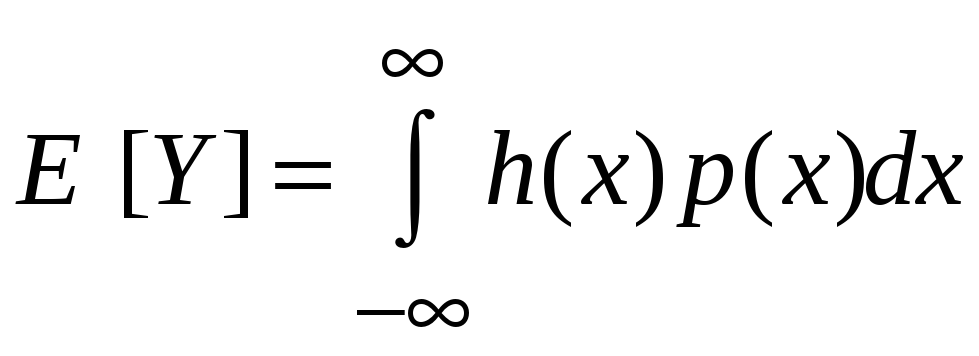 ,
в которой
,
в которой
![]() некоторая
функция, случайная величина
некоторая
функция, случайная величина
![]() определяется равенством
определяется равенством
![]() ,
а p(x)
,
а p(x)
![]() плотность распределения случайной
величины X.
Отметим, что приведенная формула для
математического ожидания
плотность распределения случайной
величины X.
Отметим, что приведенная формула для
математического ожидания
![]() не является
определением этого математического
ожидания, а доказывается с использованием
соотношений между плотностями случайных
величин X
и Y.
не является
определением этого математического
ожидания, а доказывается с использованием
соотношений между плотностями случайных
величин X
и Y.
Дисперсией непрерывной случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания, т. е.
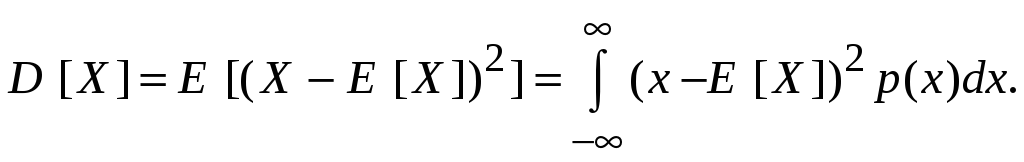
Отметим, что в этой
формуле использовано приведенное
выражение для математического ожидания
случайной величины
![]() при
при
![]()
Дисперсия случайной
величины характеризует рассеяние
(вариацию, разброс) этой величины
относительно ее математического
ожидания. Дисперсия
![]() имеет
размерность квадрата случайной величины,
что не всегда удобно. Поэтому в качестве
показателя рассеяния используют также
величину
имеет
размерность квадрата случайной величины,
что не всегда удобно. Поэтому в качестве
показателя рассеяния используют также
величину
![]() ,
называемую среднеквадратическим
отклонением
случайной величины X.
,
называемую среднеквадратическим
отклонением
случайной величины X.
Свойства дисперсии:
1. Дисперсия
константы равна нулю. Это свойство
вытекает из соотношений
![]()
2. Постоянный
множитель можно выносить за знак
дисперсии, возведя его при этом в квадрат,
т. е.
![]()
3. Дисперсия суммы
конечного числа независимых случайных
величин равна сумме их дисперсий, т. е.
![]() .
.
4. Дисперсия
случайной величины равна разности между
математическим ожиданием квадрата
случайной величины и квадратом ее
математического ожидания
![]() .
Это соотношение становится очевидным,
если раскрыть квадрат под знаком
математического ожидания в формуле,
определяющей дисперсию. ▲
.
Это соотношение становится очевидным,
если раскрыть квадрат под знаком
математического ожидания в формуле,
определяющей дисперсию. ▲
Задача 3.1. X и Y независимые случайные величины, имеющие стандартное равномерное распределение. Найти математическое ожидание и дисперсию случайной величины Z = max(X, Y).
Решение. В задаче 2.3 была получена плотность распределения случайной величины Z. Эта плотность равна
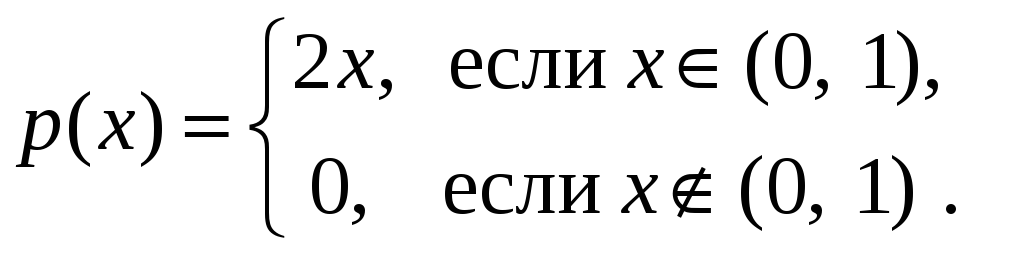
Поэтому
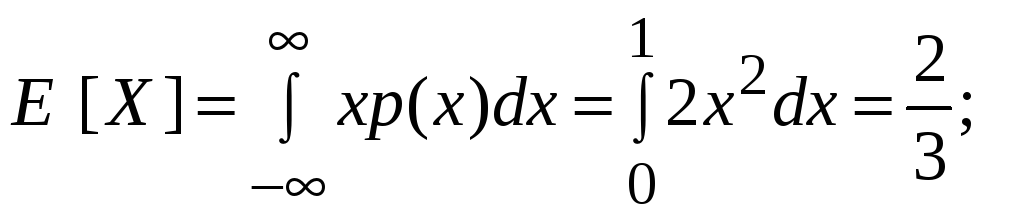
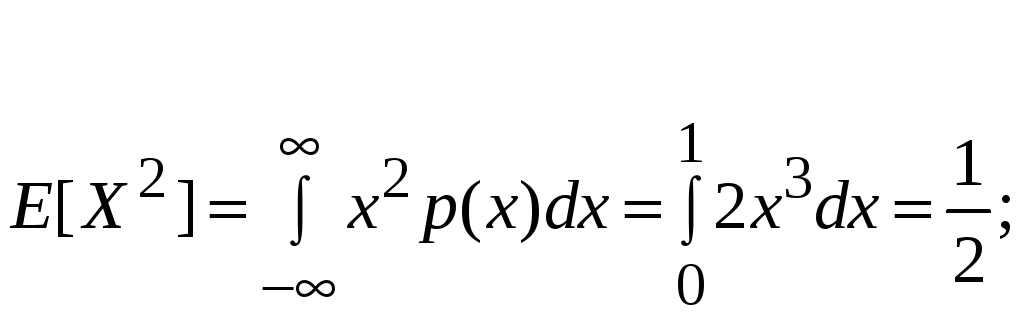
![]()
Задача 3.2.
График плотности
распределения случайной величины X
представляет
собой треугольник с вершинами в точках
(![]() 1,
0), ( 0, 1) и (1, 0).
Написать выражение для
плотности распределения и функции
распределения, найти E
[X],
D
[X].
1,
0), ( 0, 1) и (1, 0).
Написать выражение для
плотности распределения и функции
распределения, найти E
[X],
D
[X].
Решение. Плотность распределения случайной величины X имеет вид
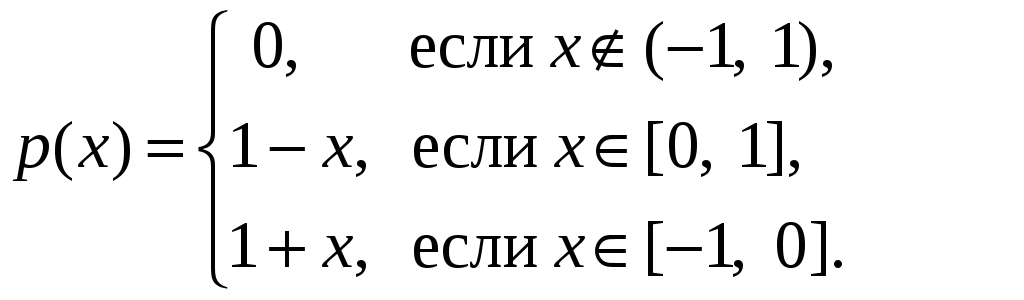
Потому, учитывая то, что функция p(x) является четной, получим
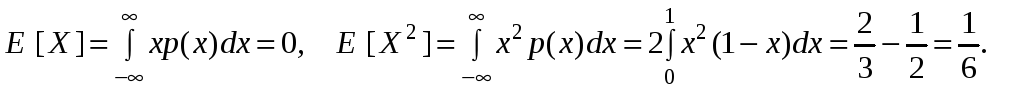 Поскольку
математическое ожидание равно нулю,
Поскольку
математическое ожидание равно нулю,
![]() = 1/6.
= 1/6.
Задача 3.3.
Пусть X
– случайная величина имеющая нормальное
распределение с параметрами
![]() т.
е. с плотностью распределения
φ
т.
е. с плотностью распределения
φ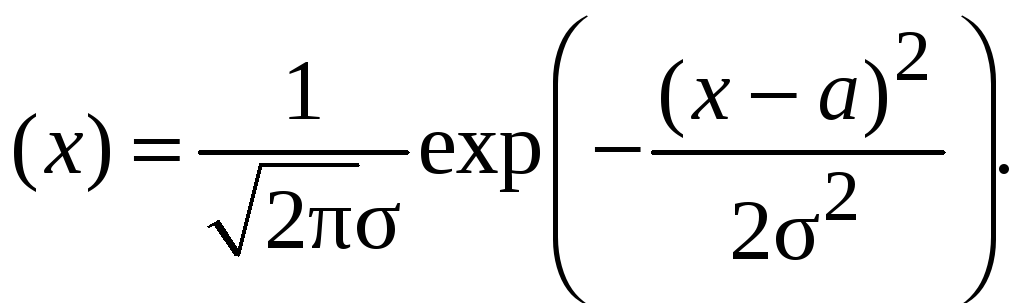 Найти E
[X]
и D
[X].
Найти E
[X]
и D
[X].
Решение. В соответствии с определением вычислим математическое ожидание:
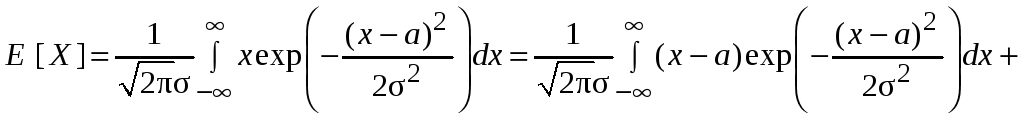
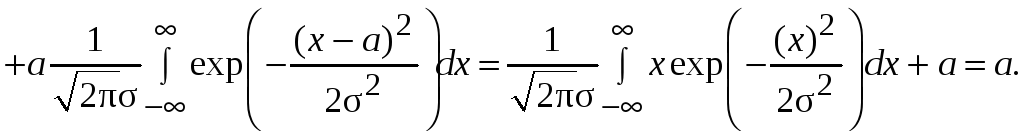
Здесь использовано
то, что
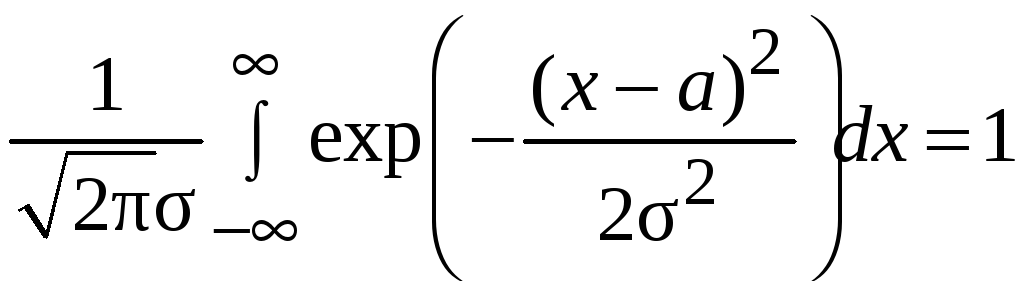 как интеграл
от плотности
нормального распределения, a
как интеграл
от плотности
нормального распределения, a
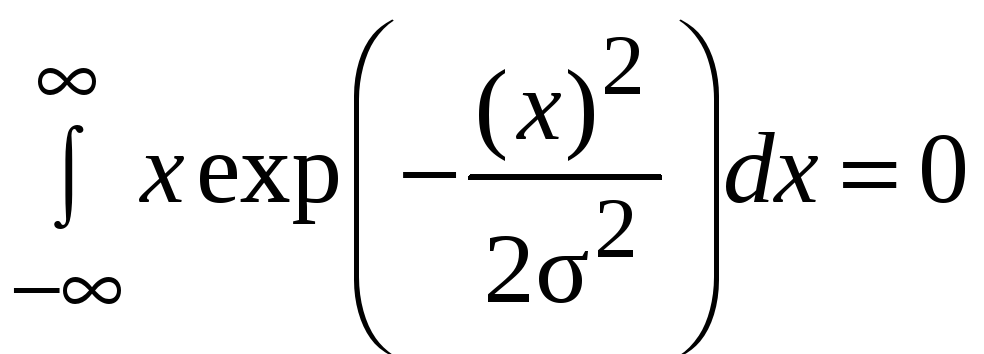 как интеграл от
нечетной функции по симметричному
множеству. Таким образом, показано, что
E
[X]
= a.
как интеграл от
нечетной функции по симметричному
множеству. Таким образом, показано, что
E
[X]
= a.
Перейдем к вычислению дисперсии.
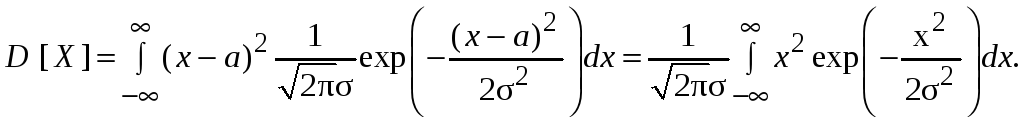
После замены
переменных
![]() и интегрирования по частям получим
и интегрирования по частям получим
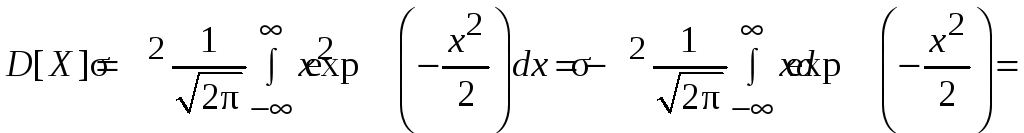
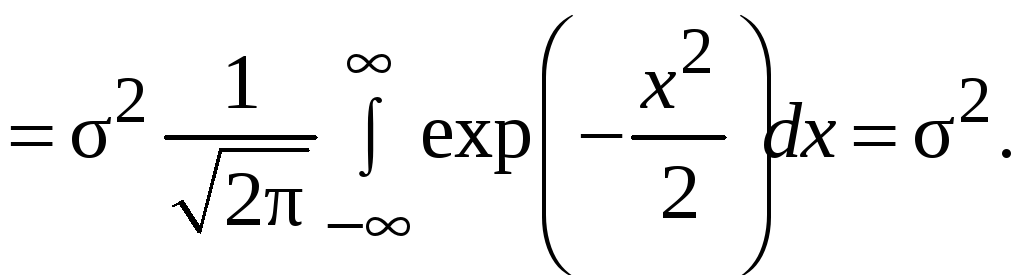
Таким образом,
![]()
Задача 3.4.
X
и Y
независимы и имеют стандартное нормальное
распределение. Определим случайные
величины U
= max(X,
Y),
V
= min(X,
Y).
Определить E
(U![]() V).
V).
Решение.
Пусть
![]() функция распределения и плотность
распределения стандартного нормального
закона. Тогда
функция распределения и плотность
распределения стандартного нормального
закона. Тогда
![]()
Поэтому плотность распределения q(x) случайной величины U равна
![]() Таким образом,
получим
Таким образом,
получим
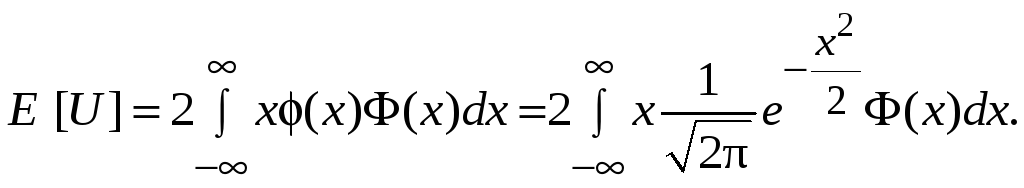
Интегрируя по частям, получим
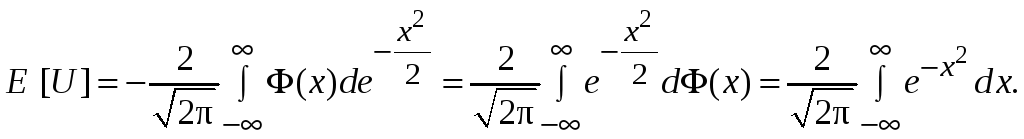
Заметим, что
нормальная случайная величина с
математическим ожиданием, равным нулю,
и дисперсией, равной
![]() ,
имеет плотность распределения
,
имеет плотность распределения
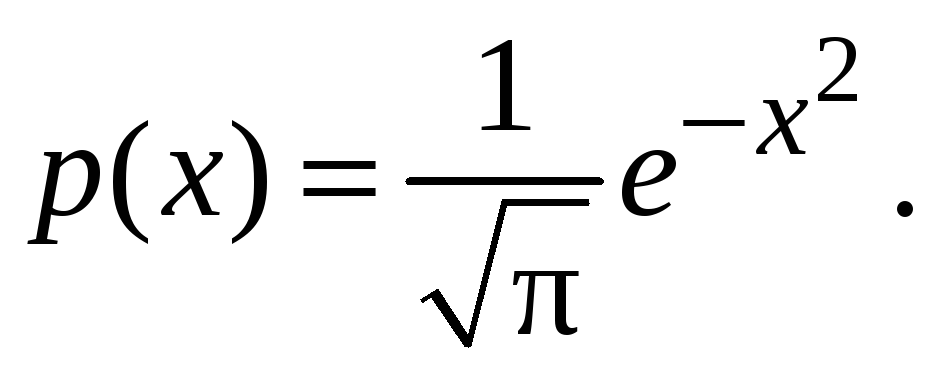 Интеграл от этой плотности распределения
равен единице. Поэтому
Интеграл от этой плотности распределения
равен единице. Поэтому
![]() Из соображений симметрии ясно, что
Из соображений симметрии ясно, что
![]() Таким образом,
Таким образом,
![]()
Задача 3.5.
Пусть случайные величины X
и Y
независимы и имеют стандартное нормальное
распределение. Определить
![]()
Решение.
Случайная величина Z
= 2X
+ 3Y
, будучи линейной
комбинацией независимых нормальных
величин, также имеет нормальное
распределение с математическим ожиданием,
равным 2 + 3 = 5, и с дисперсией, равной 4 +
9 = 13. Поэтому плотность распределения
случайной величины Z
и математическое ожидание случайной
величины
![]() равны, соответственно,
равны, соответственно,
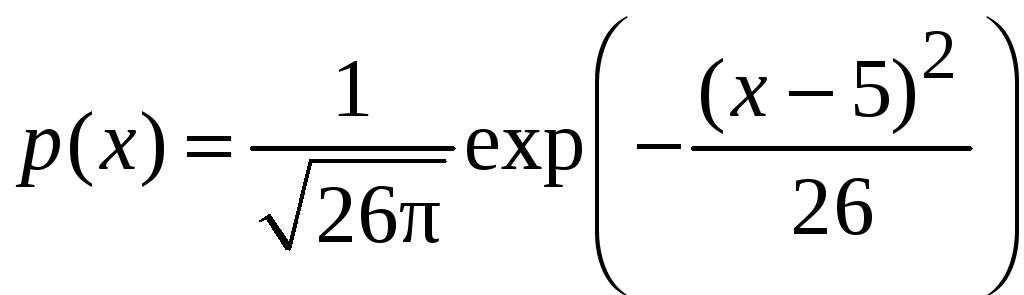 и
и
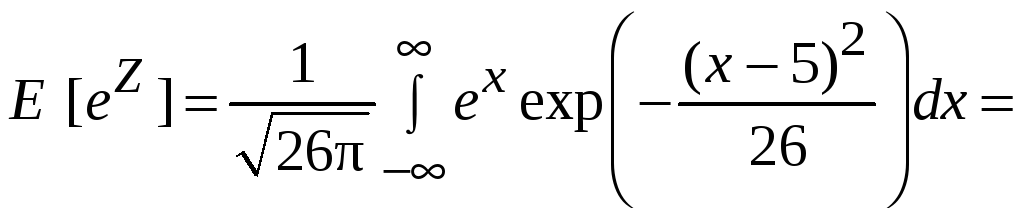
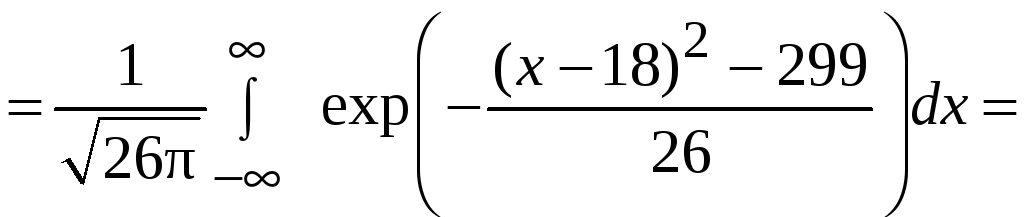
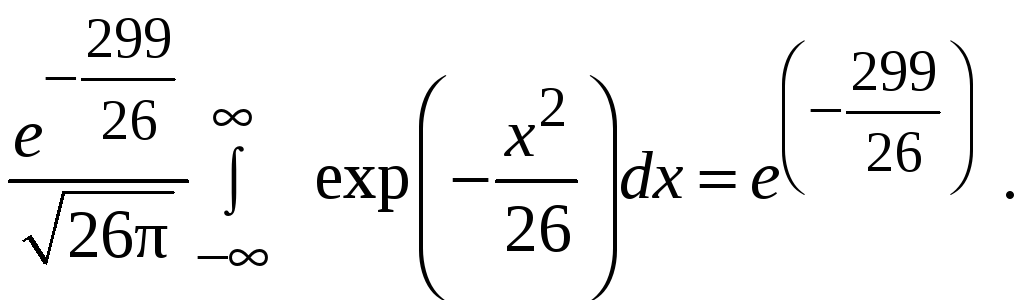
Здесь использован
тот факт, что, будучи интегралом от
плотности нормального распределения,
интеграл
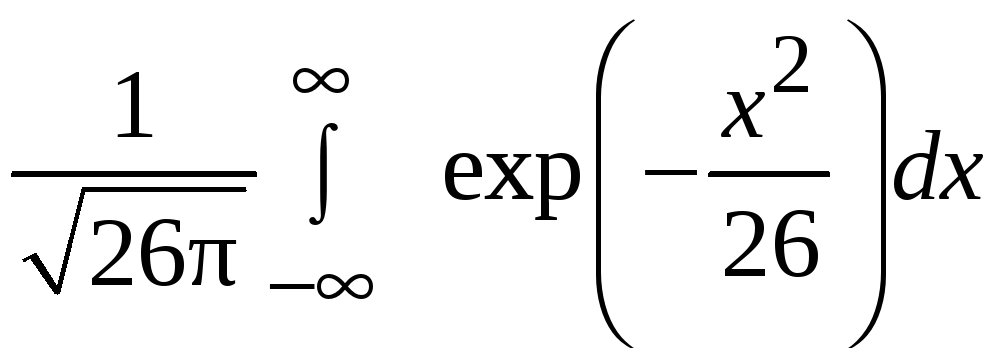 равен единице.
равен единице.
▼ Ковариацией
двух случайных величин X
и Y
называется число
![]()
![]() Его следует рассматривать как меру
линейной зависимости случайных величин
X
и
Y.
Иногда его также рассматривают как меру
стохастической зависимости X
и
Y,
но это правомерно только в том случае,
когда X
и
Y
имеют совместное нормальное распределение.
Изучение таких распределений выходит
за пределы данных методических указаний.
Его следует рассматривать как меру
линейной зависимости случайных величин
X
и
Y.
Иногда его также рассматривают как меру
стохастической зависимости X
и
Y,
но это правомерно только в том случае,
когда X
и
Y
имеют совместное нормальное распределение.
Изучение таких распределений выходит
за пределы данных методических указаний.
Перечислим свойства ковариации. Здесь a, b – вещественные числа.
1. Симметричность,
т. е.
![]()
2. Линейность, т.
е.
![]() Это свойство естественным образом
переносится на любое число слагаемых.
Это свойство естественным образом
переносится на любое число слагаемых.
3. Инвариантность
относительно сдвига, т. е.
![]()
С помощью ковариации
можно вычислять дисперсию суммы зависимых
случайных величин по формуле
![]()
Коэффициентом
корреляции
двух случайных величин X
и Y
называется число
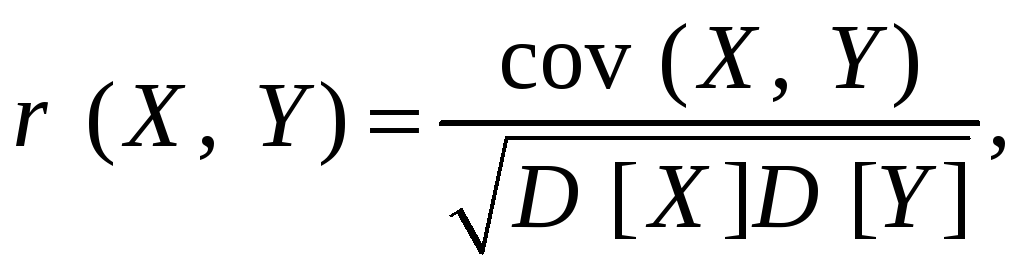 т.
е. коэффициент корреляции – это
нормированная ковариация. Перечислим
его свойства:
т.
е. коэффициент корреляции – это
нормированная ковариация. Перечислим
его свойства:
1. Симметричность,
т. е.
![]()
2. Изменения при линейных преобразованиях:
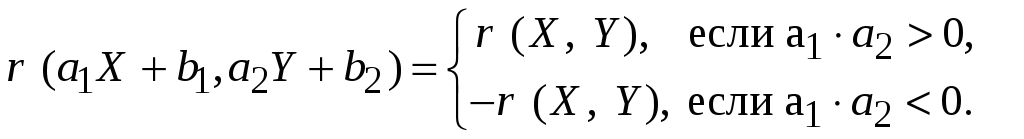
Таким образом, коэффициент корреляции сохраняется, если оба линейных преобразования возрастают или убывают одновременно. ▲
Задача 3.6. Случайный
вектор (X,
Y)
равномерно
распределен в круге
![]() Найти E
X,
D
X,
E
Y,
D
Y,
cov
(X,
Y)
и коэффициент корреляции.
Найти E
X,
D
X,
E
Y,
D
Y,
cov
(X,
Y)
и коэффициент корреляции.
Решение.
Введем случайные величины
![]() Тогда совместная плотность распределения
случайных величин
Тогда совместная плотность распределения
случайных величин
![]() равна
равна
![]() если
если
![]() и равна 0
и равна 0
![]() в противном случае. Поскольку эта
плотность является четной функцией
своих аргументов, то справедливы
равенства
в противном случае. Поскольку эта
плотность является четной функцией
своих аргументов, то справедливы
равенства
![]() Поэтому
Поэтому
![]() Остается вычислить дисперсии:
Остается вычислить дисперсии:
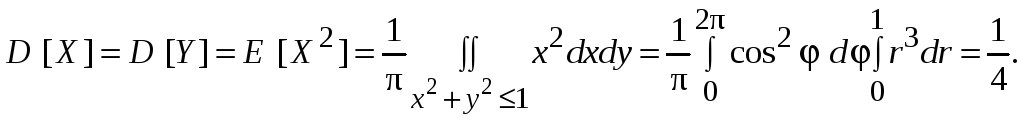
Задача 3.7. Известно, что D (X) = 1, D (Y) = 4, коэффициент корреляции равен 0.5. Найти коэффициент корреляции между 2X + Y + 1 и X + 2Y.
Решение. В соответствии с определениями ковариации и коэффициента корреляции
![]()
![]()
![]()
![]()
![]()
![]()
Поэтому искомый
коэффициент корреляции
![]()
