Тема 10. Елементи описової статистики. Емпірична функція розподілу. Гістограма.

1. Елементи описової статистики.

Нехай треба обстежити сукуп однакових об’єктів за деякою кількісною або якісною ознакою (цікавить ВВξ). Множина всіх можливих значень ξ назив. генеральною сукупністю(ГС). Вибірка з ГС об’єму n – це результати n- незалежних спостережень над ξ. Результати спостережень над ξ можна спостерігати як реалізації n – незалежних ВВ, розподілених так само, як ξ. ГС – ймовірнісний простір {Ω,s,p}і визначена на ньому ВВξ, яка називається – ознакою ГС. Вибіркою об’єму n – наз послідовність ξ1, ξ2… ξn незалежних однаково розподілених ВВ, яка співпадає з розподілом ξ.

Варіанта вибірки Х_j – це спостережене значення ВВ ξ. Статистичним рядом – наз сукупність варіант вибірки та відповідних їм частот (x_i;m_i) i= 1,k; xі є R , mі є N .

Відносні частоти(CP) – варіант вибірки W_i =

xi
wi

Інтервальним статистичним рядом(ICP) – наз сукупність частинних інтервалів зміни варіант вибірки та відповідних їм частот.(Іі, mі ), i= 1,k; Іі = [X_i, X_i+1)

m_і – кількість варіант вибірки, що потрапляють в інтервал І_і. ; W_i = ;

Іі.	[, )	[, )..	[, )
		…

2. Емпірична функція розподілу. Гістограма.

Емпірична функція розподілу є аналогом теоретичної ф-ції розподілу і визначається:

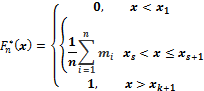
ICP:

Гістограмою (відносних) частот назив. фігура,яка склад. з прямокутників,основами яких частинні інтервали ,а висоти дорівнюють ,де -довжина частинного інтервалу

Гістограма відносних частот є аналогом графіка щільності НВВξ.

Полігон частот – називається ламана вершини якої є точки з координатами (Х_і,М_і) або (Х_і, W_i).

Для ICP (, М_і), де _– середина проміжка ₌

Тема 11. Статистичне оцінювання параметрів. Вибіркове середнє та дисперсія.

Числові хар-ки вибірки (ВВ):

1. Вибіркове середнє : нехай ми маємо вибірку об’єму n з ГС

()

Вибіркове середнє:

=

Для статистичного ряду (СР):

Вибіркове середнє: = =

Для інтервального СР: виб.сер.:

= =

2. Вибіркова дисперсія:

СР: =

ІСР:

Виправлена вибіркова дисперсія:

3. Вибіркове середнє квадратичне відхилення:

=

Виправлене середнє квадратичне відхилення:

=

4. Вибіркова мода:

СР: = , якщо мах , 1≤і≤k

ІСР: нехай [, ) – модальний інтервал (цьому інтервалу відповідають найб. частоти )

= +

5. Вибіркова медіана:

СР:

ІСР: [, ) – медіанний інтервал

= +

Емпіричні, початкові та центральні моменти:

=

=

Статистичні оцінки параметрів ГС:

Нехай задана ознака ГС , що має відомий закон розподілу з невідомими параметрами

F(x,θ), θ – невідомий параметр

()

Точковою оцінкою невідомого параметра θ назив. функція від вибірки (статистика) вигляду:

= ()

є ВВ.

Для того, щоб мала практичну цінність, вона повинна мати наступні властивості: