Уравнение, не содержащее искомой функции

Рассмотрим уравнение

или , (11)

где определена и непрерывна в интервале . Неопределенный интеграл (квадратура)

(12)

есть общее решение уравнения (11) в области

. (13)

Вся область (13) заполнена непересекающимися интегральными кривыми, каждая из которых представляет график частного решения уравнения (11).

Выберем любую точку х₀ из интервала и в качестве первообразной в формуле (12) возьмем функцию переменного верхнего предела с нижним пределом х₀, тогда общее решение (12) принимает вид

.

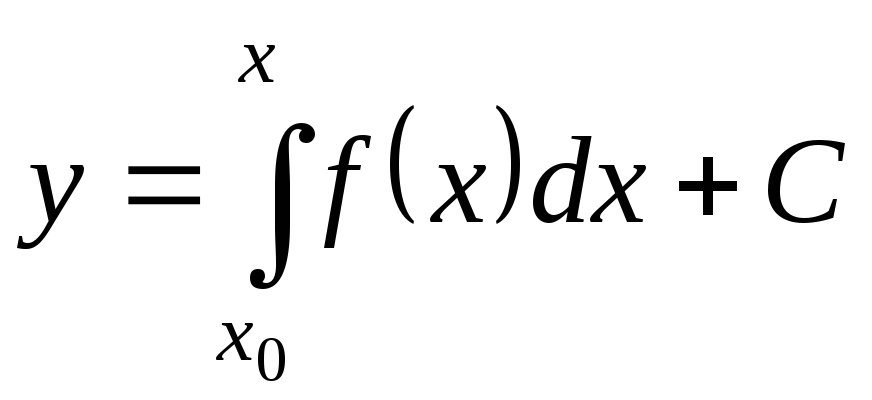Полагая здесь , , найдем , так что можно записать

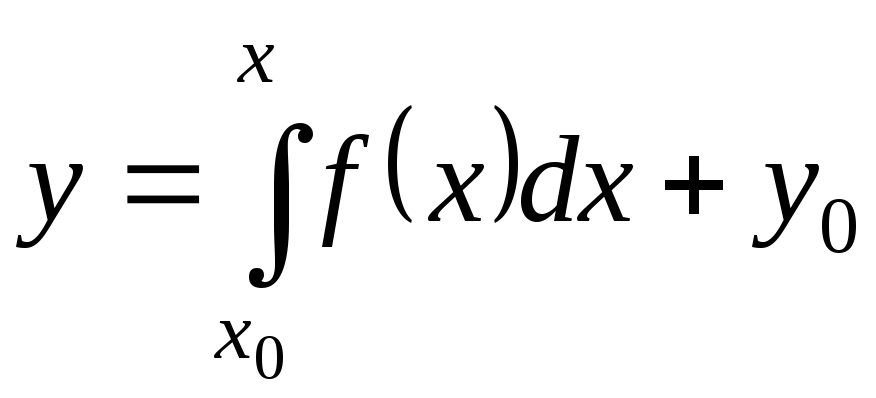. (14)

Эта формула суть решение задачи Коши с начальными данными х₀, у₀. Видно, что решение задачи Коши (функция , стоящая в левой части формулы (14)) есть непрерывно дифференцируемая функция от независимой переменной х и от начальных данных х₀ и у₀.

Если считать у₀ произвольной величиной, то формула (14) (суть неопределенный интеграл) есть общее решение в форме Коши уравнения (11) в области (13).

Пусть в уравнении (11) функция f(x) разрывна в точке , , причем именно обращается в бесконечность в этой точке и непрерывна во всех других точках, тогда формула (12) дает общее решение уравнения (11) в каждой из областей и ; (рис. 6).

Прямая является решением перевернутого уравнения

и должна быть присоединена к решению уравнения (11). Это решение может оказаться особым, если в каждой его точке нарушается единственность, как показано на рис. 6, а. Оно будет частным, если единственность сохраняется во всех точках (рис. 6, б).

Прямая по отношению к семейству интегральных кривых, образующих общее решение, может быть или огибающей и тогда – особое решение, или асимптотой, тогда – частное решение.

Примеры.

10. , , . Правая часть уравнения определена и непрерывна в каждом из интервалов , и обращается в бесконечность в точке х = 0. Общее решение находим по формуле (12)

в каждой из областей и . Прямая х = 0 является решением перевернутого уравнения, она является асимптотой интегральных кривых и потому частным решением рассматриваемого уравнения.

11. . Правая часть уравнения определена и непрерывна в интервале (–1, +1). В области , находим общее решение . Прямые – особые решения рассматриваемого уравнения, они являются огибающими семейства .

Уравнение, не содержащее независимой переменной

Рассмотрим уравнение

, (15)

где функция f(y) определена и непрерывна в интервале и нигде на этом интервале не обращается в нуль. Тогда в горизонтальной полосе

(16)

квадратурой немедленно находим общий интеграл

; (17)

этот же интеграл можно записать в форме Коши

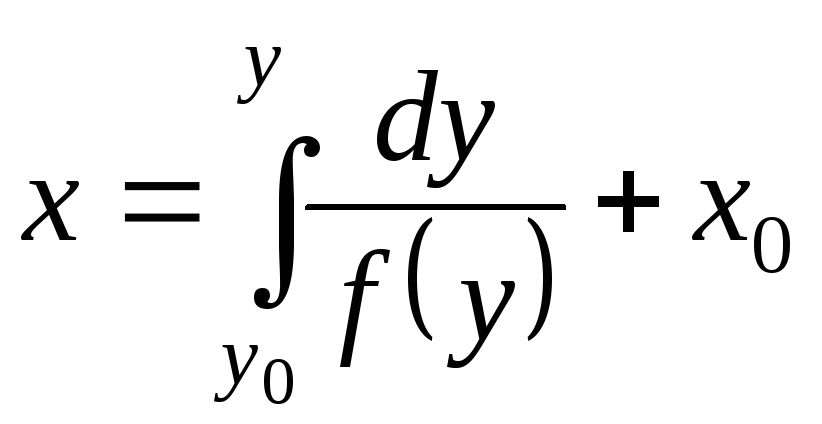, (18)

где х₀ считается произвольной постоянной, а у₀ – фиксированное число, .

Для уравнения (15) перевернутым уравнением будет

.

Уравнение не содержит искомой функции х, поэтому к нему применимо все сказанное относительно уравнения (11), в частности, по поводу особых решений.

Если f(y) обращается в нуль в некоторой точке из интервала , то прямая всегда является решением уравнения (15). Это решение будет особым, если – огибающая семейства кривых (17).

Заметим, что нахождение решения задачи Коши с начальными условиями при для уравнения (15) эквивалентно нахождению решения интегрального уравнения

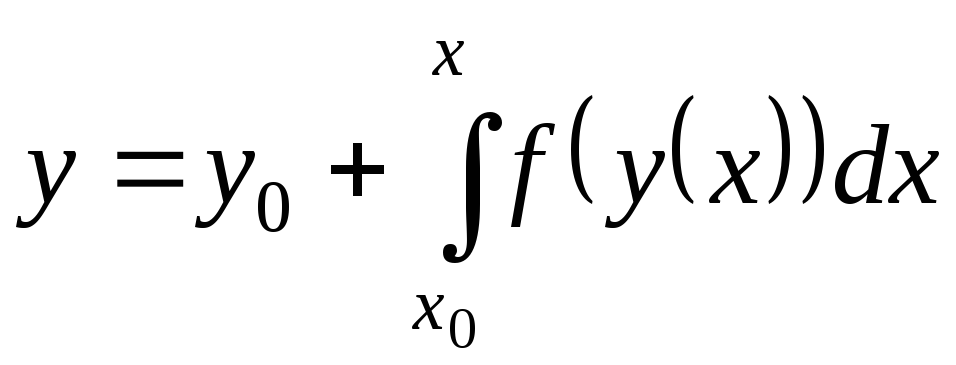. (19)

Уравнение с функцией специального вида

, (20)

где определена и непрерывна в некоторой области D, с помощью подстановки (замены неизвестной функции новой)

, , , (21)

приводится к уравнению вида (15).

Примеры.

12. . Правая часть данного уравнения определена и непрерывна при всех значениях у и обращается в нуль при . Разделяя переменные, квадратурой

, , находим .

Это выражение является общим интегралом уравнения, при его нахождении использовалась табличная формула (на математическом сленге «высокий логарифм»)

.

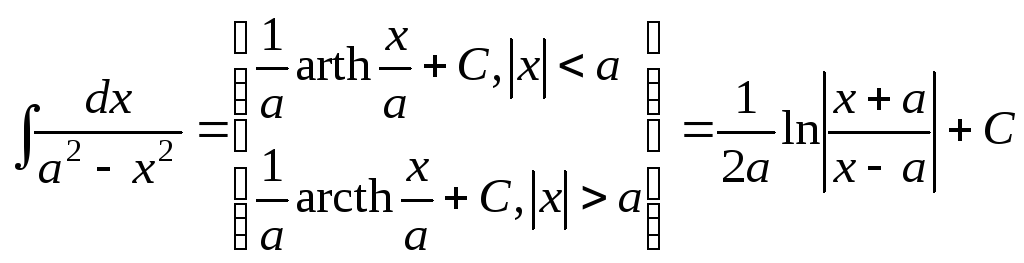Здесь arth x и arcth x – арктангенс и арккотангенс гиперболические – являются обратными по отношению к прямым гиперболическим функциям, соответственно:

и .

Если обозначить прямую функцию как оператор , а обратную – , то в области их существования D (там, где они непрерывны и монотонны) справедливы тождества

.

Используя эти тождества и учитывая логарифмические представления

,

,

из общего интеграла немедленно находим общее решение данного уравнения

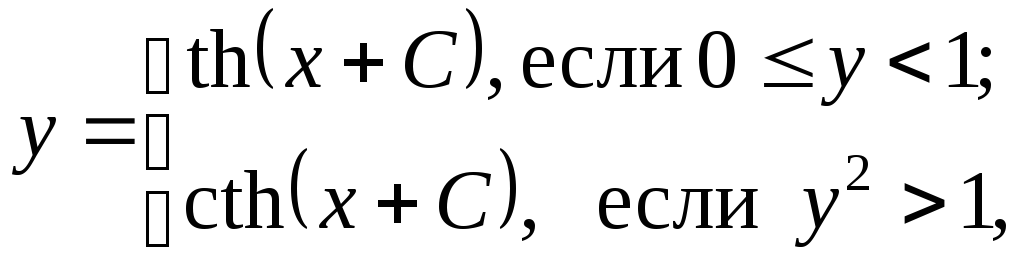
из которого следует, что линии являются горизонтальными асимптотами интегральных кривых и потому – частотными решениями (рис. 7). При графическом представлении общего интеграла данного уравнения, следует учесть, что гиперболический котангенс имеет еще и вертикальную асимптоту при равном нулю аргументе (рис. 7).

13. Проинтегрировать уравнение с начальными условиями:

а. , ; б. .

Запишем данное уравнение в виде . Предполагая , разделим переменные

.

Интегрируем в форме Коши (18)

.

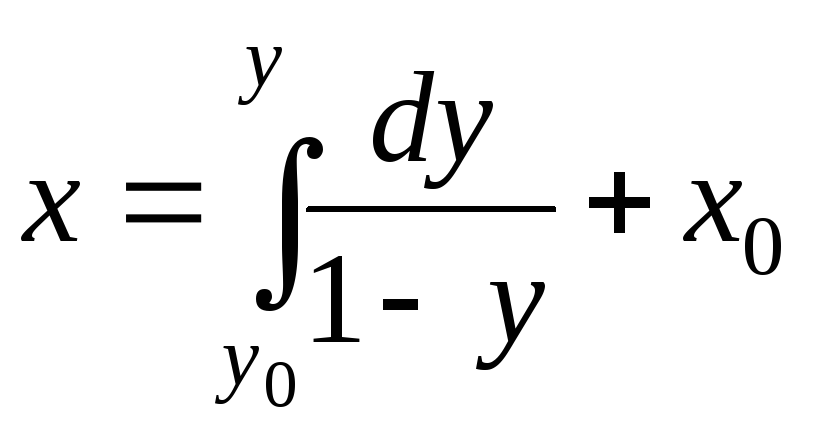Внесением под знак дифференциала

,

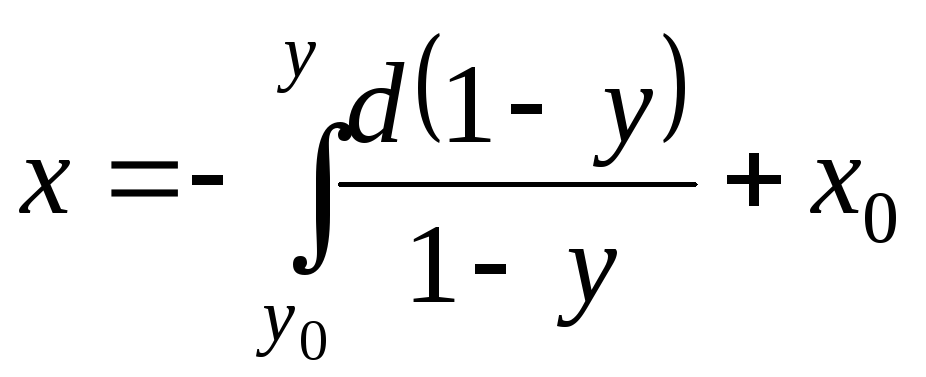непосредственно интегрируем, с использованием формулы Ньютона–Лейбница

,

преобразуем .

Потенцируя и преобразуя, выразим искомую функцию через независимую переменную х и параметры х₀ и у₀

.

Это и есть общее решение данного уравнения в форме Коши, доставляющее частные решения соответствующих задач Коши прямой подстановкой начальных данных. Решения поставленных задач имеют вид (они показаны на рис. 8):

а. ; б.

Для графического построения общего интеграла удобно пользоваться формулой (17), «не убирая» постоянную С от переменной х. Для рассматриваемого уравнения она имеет вид

, или интегрируя, .

Потенцируя и освобождаясь от знака модуля, находим общее решение

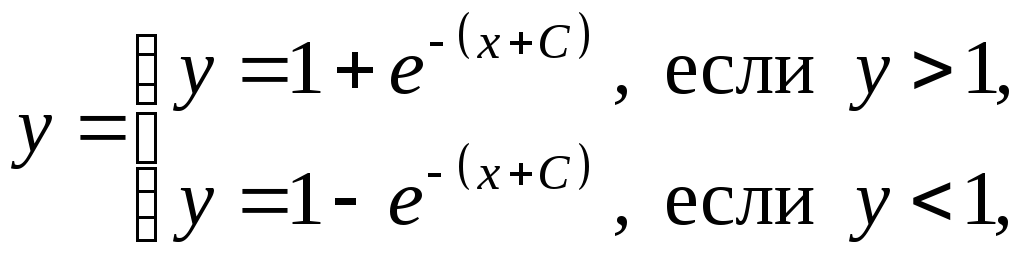
из которого можно получить решение задачи Коши. В полуплоскости (верхнее выражение для общего решения) заданы начальные условия а), а в полуплоскости (нижнее выражение) заданы условия б). Заменяя переменные х и у в общем решении (общем интеграле) их начальными значениями х₀ и у₀, решаем полученное уравнение относительно неизвестной константы С. Найденное значение снова подставляем в общее решение (или интеграл) и тем самым осуществляем выбор частного решения – единственного решения задачи Коши. Для рассматриваемого примера эти действия выглядят так:

а. , , ;

б. , , .

Из вида общего решения (эскиз показан на рис. 8) следует, что линия является частным решением.

14. . Здесь правая часть определена и непрерывна в интервале и обращается в нуль на концах этого интервала. Квадратурой по формуле (17) находим общий интеграл

,

в полосе .

Применяя к обеим частям общего интеграла оператор (см. пример 12), получаем общее решение

, .

Линии являются огибающими данного семейства и потому особыми решениями (рис. 9).

1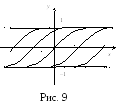5. . Это линейное уравнение относительно неизвестной функции и ее производной. Подстановкой , приводим его к уравнению вида (20)

, ,

которое с помощью подстановки (21)

,

приводится к уравнению . Это уравнение вида (15), его правая часть обращается в нуль на линии . Согласно формуле (17), находим общий интеграл и из него, потенцируя, общее решение

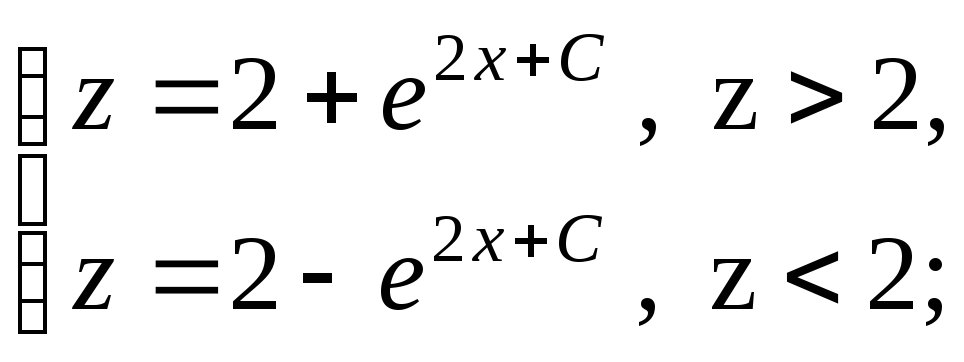
видно, что прямая является общим решением. Последовательно возвращаясь к старым переменным, находим общее решение промежуточного уравнения

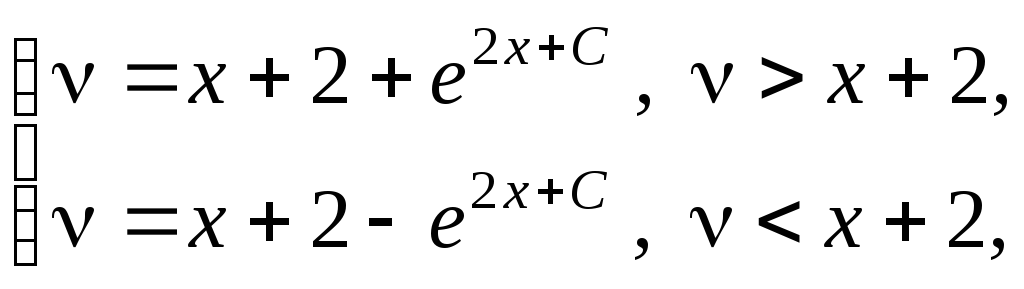
(из которого видно, что прямая является частным решением промежуточного уравнения) и общее решение исходного уравнения в виде

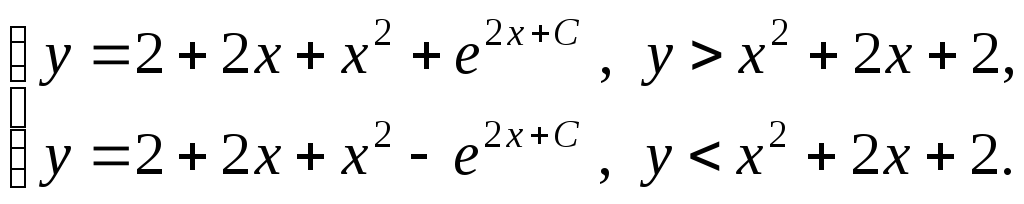
Анализируя процесс получения этого решения, замечаем, что оно состоит из двух частей: частного решения – параболы и общего решения уравнения – функции . С другой стороны, заново решая уравнение (по-другому выбирая расположение произвольной постоянной С)

, , ,

, , ,

находим общее решение исходного уравнения

в более удобном для аналитических целей виде. Аналогичным образом может быть пересмотрено общее решение в примере 13.

16. Найти решение интегрального уравнения .

Это уравнение типа (19). Дифференцируя по х обе его части и учитывая, что производная от функции переменного верхнего предела равна подынтегральной функции, получаем задачу Коши. Найти единственное решение уравнения

, удовлетворяющее условиям у = 1 при х = 0.

Записывая общий интеграл дифференциального уравнения в форме Коши (18) и вычисляя, находим искомое решение

, .

17. . Это нелинейное уравнение вида (20), заменой переменных (21) его можно свести к уравнению вида (15) и найти общий интеграл. Но лучше рассмотреть перевернутое уравнение , которое суть линейное относительно неизвестной функции и ее производной; оно той же заменой сводится к уравнению вида (15). Как известно, внешне различные, общие интегралы прямого и перевернутого уравнений выражают одно и то же геометрическое место точек.

Найдем общий интеграл рассматриваемого уравнения, переходим к перевернутому

, , , , ,

, , .