4. Электромагнитные колебания.

4.1 Основные понятия и законы.

Электрическим колебательным контуром называется замкнутая электрическая цепь, содержащая конденсатор емкости С и катушку индуктивности L.

Если омическим сопротивлением такого контура можно пренебречь, то его называют идеальным, а колебания в контуре происходят по синусоидальному закону:

.

ω – собственная частота колебаний, определяется по формуле Томсона:

Сила тока в контуре изменяется по закону

где I₀= q₀·ω – амплитуда силы тока.

Колебания тока опережают по фазе колебания заряда в контуре на π/2.

Уравнение колебаний напряжения на конденсаторе имеет вид:,

где U₀ = q₀/C – амплитуда напряжения.

Амплитуда колебаний тока связана с амплитудой колебаний напряжения соотношением:

.

Полная энергия контура равна сумме энергий электрического поля конденсатора и магнитного поля катушки:

.

В идеальном колебательном контуре полная энергия сохраняется.

В контуре, содержащем конденсатор емкости С, катушку индуктивности L и активное сопротивление R, соединенные последовательно, происходят затухающие колебания по закону:

,

где – коэффициент затухания,

- частота затухающих колебаний.

Если в колебательном контуре, содержащем конденсатор емкости С, катушку индуктивности L и активное сопротивление R, соединенные последовательно, действует периодическая ЭДС , то в нем возникают вынужденные колебания с частотой ЭДС – ω_в.

При этом установившиеся колебания силы тока имеют вид:

,

где, .

Если в цепи течет переменный ток, то для расчета такой цепи можно применять закон Ома. Всякая реальная цепь обладает конечными сопротивлением R, емкостью С и индуктивностью L. Полное электрическое сопротивление такой цепи называется импедансом и находится по формуле:

где ω = 2πυ – циклическая частота переменного тока,

- индуктивное сопротивление,

- емкостное сопротивление.

Постоянному току индуктивность не оказывает сопротивление, а емкостное сопротивление для постоянного тока равно бесконечности, постоянный ток через конденсатор не течет.

Средняя мощность, выделяемая в цепи переменного тока, рассчитывается по формуле:,

где cosφ₁ называется коэффициентом мощности переменного тока.

Как правило используют действующие(эффективные) значения силы тока и напряжения:

.

Тогда выражение для средней мощности имеет вид:

.

4.2. Примеры решения задач.

1. Задача на идеальный колебательный контур.

Колебательный контур состоит из конденсатора емкостью С=5 мкФ и катушки индуктивности L = 0,2 Гн. Определить максимальную силу тока I₀ в контуре, если максимальная разность потенциалов на обкладках конденсатора U₀ = 90 В. Активным сопротивлением проводов в контуре пренебречь.

Запишем краткое условие задачи.

Решение:

Воспользуемся законом сохранения энергии для идеального колебательного контура:

Д ано: СИ

L=0,2 Гн

С=5 мкФ =5·10^-6Ф

U₀= 90В

I₀ -?

Полная энергия контура равна энергии конденсатора при максимальном значении U: .

Сила тока достигает максимального значения в момент разрядки конденсатора, при этом .

Следовательно, .

Откуда: .

Произведем вычисления: .

Ответ: 0,45 А

2. Задача на формулу Томсона.

В колебательный контур включен конденсатор емкостью С=0,2 мкФ. Какую индуктивность L нужно включить в контур, чтобы получить в нам электромагнитные колебания частоты υ = 400Гц?

Запишем краткое условие задачи.

Решение:

Воспользуемся формулой Томсона: .

Циклическая частота равна

ω = 2πυ

Д ано: СИ

С=0,2 мкФ =0,2·10^-6Ф

υ= 400Гц

L -?

Следовательно, .

Откуда

Произведем вычисления: .

Ответ: 0,79 Гн.

3. Задача на переменный ток.

В цепи, состоящей из последовательно соединенных резистора сопротивлением R = 200 Ом, конденсатора емкостью C = 100 мкФ, катушки индуктивностью L = 0,2 Гн, протекает переменный ток частотой υ = 50 Гц. Найдите среднюю мощность тока. Амплитуда приложенного напряжения U_m = 300 В.

Запишем краткое условие задачи.

Решение:

Мощность тока найдем по формуле.

Причем

Д ано: СИ

R = 200 Ом

L = 0,2 Гн

С=100 мкФ =10^-4Ф

υ= 50Гц

U_m = 300 В

Р -?

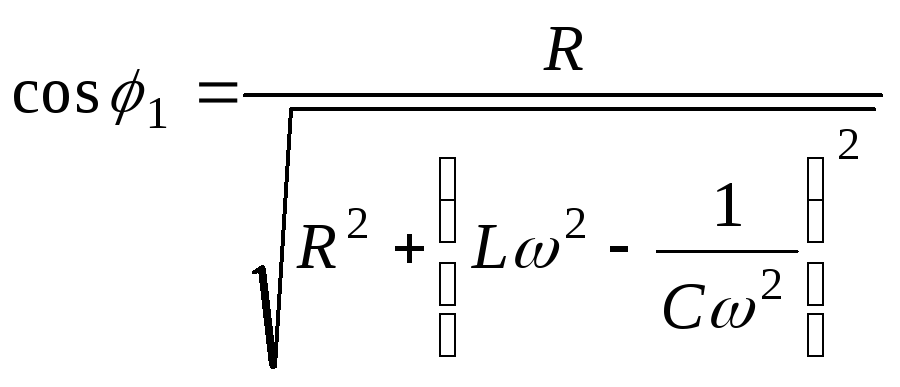
ω = 2πυ

Следовательно, .

Произведем вычисления:

.

Ответ: 0,14·10^-2 Вт.