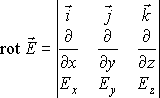1) Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Электрический заряд обычно обозначается буквами q или Q.

Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

Тот факт, что электрический заряд встречается в природе лишь в виде целого числа элементарных зарядов, можно назвать квантованием электрического заряда. При этом в классической электродинамике вопрос о причинах квантования заряда не обсуждается, поскольку заряд является внешним параметром, а не динамической переменной.

Зако́н Куло́на — это закон о взаимодействии точечных электрических зарядов.Был открыт Шарлем Кулоном в 1785 г.

При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:

А)Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.

Б)Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.

В)Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.

Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.

2) Электрическое поле — одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может наблюдаться благодаря его силовому воздействию на заряженные тела.

Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

.

Напряжённость поля точечного заряда:

ПРИНЦИП СУПЕРПОЗИЦИИ ( НАЛОЖЕНИЯ ) ПОЛЕЙ:

Если в данной точке пространства различные электрически заряженные частицы 1, 2, 3... и т.д. создают электрические поля с напряженностью Е1, Е2, Е3 ... и т.д., то результирующая напряженность в данной точке поля равна геометрической сумме напряженностей.

Силовой линией (векторной линией или интегральной кривой, в зависимости от контекста) для поля называется кривая , касательная к которой во всех точках кривой совпадает со значением поля:

Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.

3) Энергия W взаимодействия системы точечных зарядов Q(1), Q(2), ..., Q(n) определяется работой, которую эта система зарядов может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой:

,

где ф(i) — потенциал поля, создаваемого всеми п–1 зарядами (за исключением 1-го) в точке, где расположен заряд Q(i).

Потенциал поля - это энергетическая характеристика поля, характеризует потенциальнную энергию, которой обладал бы положительный единичный заряд, помещенный в данную точку поля.

Потенциал электрического поля, создаваемый точечным зарядом Q на расстоянии r от заряда,

.

РАЗНОСТЬ ПОТЕНЦИАЛОВ электрическая (для потенциального электрического поля то же, что напряжение электрическое) между двумя точками пространства (цепи); равна работе электрического поля по перемещению единичного положительного заряда из одной точки поля в другую.

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

E = - grad = -Ñ.

4) Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N(E).

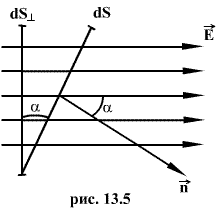
Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).

где - угол между силовой линией и нормалью к площадке dS; - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

Теорема Гаусса для напряженности электростатического поля

Пусть в некоторой области пространства известно векторное поле напряженности электростатического поля . Допустим, что в окрестности фиксированной точки пространства имеется элемент поверхности площади , ориентацию которого можно задать с помощью вектора единичной (безразмерной) нормали к этому элементу поверхности. Поскольку элемент поверхности является двусторонним объектом, то направление нормали можно выбрать произвольно. Введем в рассмотрение объект

(1.42)

вектор элемента площади поверхности. В соответствии с (1.42) этот вектор численно равен площади элемента поверхности, имеет размерность площади и направлен вдоль , то есть вдоль нормали к элементу поверхности.

Элемент потока вектора через площадку по определению равен скалярному произведению вектора и вектора :

. (1.43)

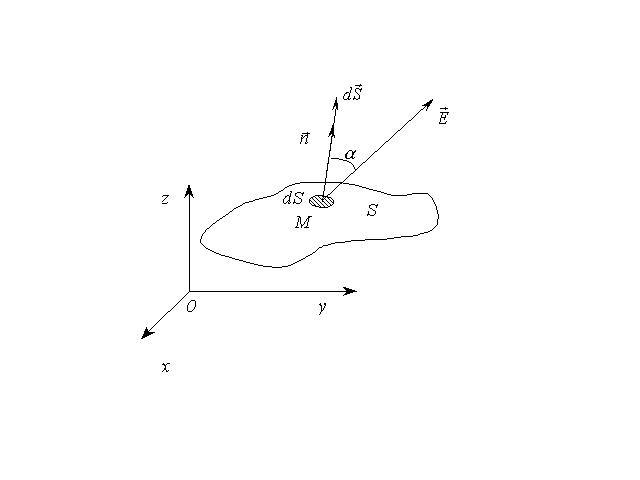
Элементарный поток вектора напряженности электростатического поля

Угол в выражении (1.43) измеряется между направлением вектора и направлением нормали к площадке . При , то есть при , значение элемента потока вектора максимально, а при элемент потока обращается в нуль. Это свойство элемента потока легко понять, если привлечь понятие силовой линии векторного поля. В первом случае силовые линии перпендикулярны площадке , а во втором случае они "скользят" вдоль

Рис. 1.6.

площадки, не пересекая ее. Заметим, что , если угол - тупой.

Если рассматривать поверхность конечных (или бесконечных) размеров, то можно определить поток вектора через эту поверхность:

(1.44)

В определении (1.44) подразумевается, что поверхность достаточно гладкая, направления нормалей к двум соседним элементам поверхности не сильно различаются между собой. Последнее означает, что все элементы поверхности построены "на одной стороне" поверхности . В случае бесконечных размеров поверхности , а иногда и для поверхности конечных размеров, встает вопрос о существовании интеграла (1.44).

Если поверхность является замкнутой поверхностью, то, как правило, поток вектора через поверхность рассчитывают с использованием внешней нормали по отношению к объему, заключенному внутри поверхности :

(1.45),

где кружок у интеграла означает, что поверхность - замкнутая.

Поток вектора напряженности электростатического поля через замкнутую поверхность обладает специфическим свойством: его величина пропорциональна электрическому заряду, расположенному внутри этой поверхности. Это утверждение составляет физический смысл теоремы Гаусса. Теорема Гаусса для вектора напряженности электростатического поля в вакууме является следствием закона Кулона. Теорема Гаусса имеет большое значение в теории электромагнетизма.

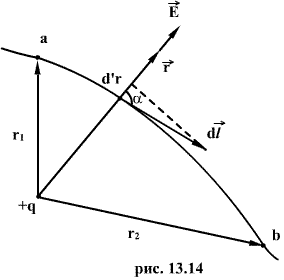
5) Работа перемещения заряда в электростатическом поле равна

или

Условие потенциальности электростатического поля для любого контура l

(1.26)

Заметим, что условие (1.26) будет выполнено, если дифференциальная форма Пфаффа является полным дифференциалом. Последнее влечет за собой необходимость выполнения совокупности условий:

Условия (1.27) можно компактно записать в векторной форме, если ввести в рассмотрение вектор "ротор" напряженности электрического поля :