6. Економічні проблеми, що призводять до необхідності застосування оптимізаційних моделей. Приклади проблемних ситуацій та відповідних ним моделей.

7. Геометрична інтерпретація задачі лінійного програмування.

Коли ЗЛП містить лише дві змінні (), неважко отримати її геометричну інтерпретацію і розв’язати задачу графічним способом.

Геометричний образ цільової функції – це сукупність паралельних прямих , для яких вектор нормалі (градієнт) указує напрям зростання значень цільової функції.

Якщо D обмежена многокутником, то задача розв’язувана, оптимальний розвязок або єдиний (у вершині), або знаходиться на стороні многокутника.

Якщо вектор нормалі дозволяє необмежено рухати цільову функцію вздовж області D, то цільова функція буде набувати будь-яких великих значень і буде необмеженою на D.

8. Графічний метод розв'язання задачі лінійного програмування.

На геометричній інтерпретації базується графічний метод розв’язування ЗЛП.

Алгоритм:

1. Побудова прямих, які відповідають рівнянням обмежень.

2. Визначення півплощин, що відповідають кожному обмеженню.

3. Визначення багатокутника D

4. Побудова вектора нормалі

5. Побудова прямої, що відповідає цільовій функції

6. Переміщення прямої в напрямі вектора нормалі для задач на максимум. Знаходження вершини D.

7. Визначення оптимальної точки та оптимуму.

9. Алгоритм симплекс-методу.

Алгоритм симплекс-методу застосовується для КЗЛП:

,

,

,

де і .

Припустимо, що КЗЛП невироджена і ранг матриці дорівнює , тобто усі рівняння-обмеження задачі лінійно незалежні. Нехай відомий який-небудь базисний розв’язок цієї задачі і вектори утворюють базис, так що і .

Алгоритм симплекс-методу складається з таких процедур:

1. Розкладаються вектори 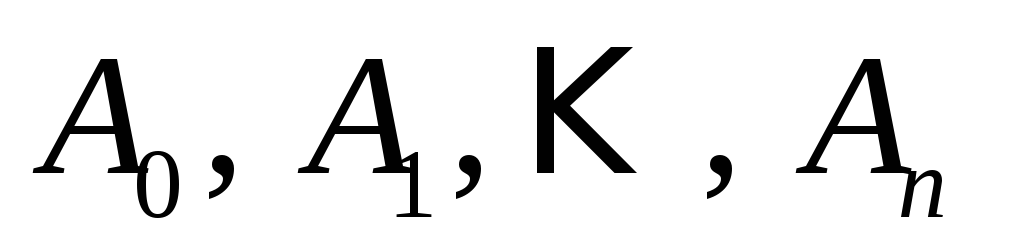за базисом .

2. Для кожного обчислюємо оцінку

.

Якщо всі , тоді даний базисний розв’язок оптимальний. Оптимальне значення цільової функції . Кінець алгоритму.

Якщо є хоча б одна від’ємна оцінка , тоді переходимо на 3-й крок.

3. З’ясовуємо, чи існує хоча б одна оцінка , для якої всі .

Якщо така оцінка існує, тоді цільова функція КЗЛП необмежена зверху на допустимій множині. Кінець алгоритму.

Якщо ж таких оцінок немає (тобто для будь-яких є хоча б одна координата ), тоді переходимо на 4-й крок.

4. Вибираємо одну з . Нехай це буде і підраховуємо відношення для усіх , таких що .

Знаходимо мінімальне з цих відношень (нехай це буде -те відношення):

.

5. Переходимо до нового базисного розв’язку, базис якого отримується заміною вектора на .

Координати усіх векторів у новому базисі підраховуємо за формулами:

,

.. Повертаємося на 2-й крок алгоритму.

10. Основні теореми симплекс-методу.

Теорема 1 (критерій оптимальності базисного розв’язку):

Якщо для даного базисного розв’язку всі оцінки , то цей розв’язок оптимальний.

Доведення. Нехай — базисний розв’язок,— його базис і , тобто . Візьмемо інший допустимий розв’язок . Якщо б інших допустимих розв’язків не було, тоді єдиний допустимий розв’язок і був би оптимальним. Покажемо, що.

Оскільки і , то .

(1.4.12)

Оскільки — допустимий розв’язок, то .

Але і .

Але ж — також допустимий розв’язок, то .

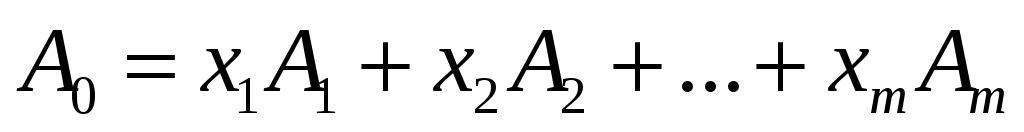Оскільки розклад будь-якого вектора по базису єдиний, то .

Підставляючи це в (1.4.12), дістанемо , що і треба було довести.

Теорема 2 (ознака необмеженості цільової функції)

Якщо для якого-небудь базисного розв’язку існує хоча б одна оцінка така, що для неї всі, то це означає, що цільова функція ЗЛП не обмежена зверху на допустимій множині.

Доведення.

Нехай, наприклад, — базисний розв’язок, для якого виконані умови теореми, і .

Розглянемо вектор з координатами , де - довільне додатне число.

Вектор має невід’ємні координати і, крім того, задовольняє обмеженням задачі, тобто є допустимим для даної ЗЛП. Дійсно

.

Підрахуємо тепер значення цільової функції для побудованого допустимого розв’язку

.

(1.4.13)

Оскільки , то згідно (1.4.13) цільову функцію можна збільшувати необмежено, залишаючись у допустимій області. Теорему доведено.

Теорема 3 (про можливість поліпшення базисного розв’язку)

Якщо для даного невиродженого базисного розв’язку задачі (1.4.1) існує така від’ємна оцінка , що серед координат вектора у даному базисі є додатні, тоді базис, якому відповідає кращий базисний розв’язок (з більшим значенням цільової функції), отримується заміною вектором того вектора початкового базису, для якого .