6.7 Аппроксимация и интерполяция данных
Пусть зависимость между переменными величинами x и y выражается в виде экспериментально полученной таблицы:
|
xi |
x0 |
x1 |
… |
xn-1 |
xn |
|
yi |
y0 |
y1 |
… |
yn-1 |
yn |
Если аналитическое выражение зависимости y = f(x) неизвестно или очень сложно, то возникает задача аппроксимации, т.е. задача нахождения такой достаточно простой функции y = F(x), значения которой на отрезке [a;b], содержащем точки xi, i = 0,…, n, возможно мало отличаются от значений искомой функции. Требование точного совпадения yi = F(xi) приводит к задаче интерполирования.
Полиномиальная аппроксимация измерений, которые сформированы как некоторый вектор Y, при значениях аргумента, которые образуют вектор X такой же длины, что и Y, осуществляется командой polyfit(X,Y,n) по методу наименьших квадратов. Здесь n – порядок аппроксимирующего полинома. Результатом действия этой процедуры является вектор длины (n+1) коэффициентов аппроксимирующего полинома.
Пусть функция f(x) задана таблично:
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
1.1 |
0.2 |
0.5 |
0.8 |
0.7 |
0.6 |
0.4 |
0.1 |
Применяя команду polyfit при различных значениях порядка аппроксимирующего полинома, получим:
>> x=1:8;
>> y=[-1.1 .2 .5 .8 .7 .6 .4 .1];
>> p1=polyfit(x,y,1)
p1 =
0.1143 -0.2393
>> p2=polyfit(x,y,2)
p2 =
-0.1024 1.0357 -1.7750
>> p3=polyfit(x,y,3)
p3 =
0.0177 -0.3410 1.9461 -2.6500
>> p4=polyfit(x,y,4)
p4 =
-0.0044 0.0961 -0.8146 3.0326 -3.3893
Это означает, что заданную табличную зависимость можно аппроксимировать:
прямой y(x) = 0,1143x – 0,2393;
квадратной параболой y(x) = -0,1024x2+1,0357x – 1,7750;
кубической параболой y(x) = 0,0177x3 – 0,3410x2+1,9461x – 2,6500;
или параболой четвертой степени
y(x) = -0.0044x4+0.0961x3 - 0.8146x2+3.0326x - 3.3893.
Построим в одном графическом окне графики заданной дискретной функции и графики трех первых полученных при аппроксимации полиномов:
>> plot(x,y,'ko');
>> hold
>> x1=.5:.05:8.5;
>> y1=polyval(p1,x1);
>> y2=polyval(p2,x1);
>> y3=polyval(p3,x1);
>> plot(x1,y1,'k-',x1,y2,'g.',x1,y3,'b:')
>> legend('table','n=1','n=2','n=3')
>> grid
В результате получается график, изображенный на рис. 6.6.
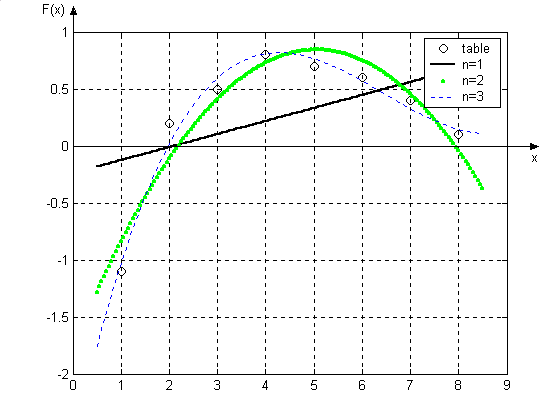
Рис. 6.6
Одномерную табличную интерполяцию производит команда interp1. Обращение к ней в общем случае имеет вид Yi=interp1(X,Y,Xi, метод) и позволяет дополнительно указать метод интерполяции в четвертом аргументе: nearest – ступенчатая интерполяция; linear – линейная; spline – кубическими сплайнами. Она интерполирует значения вектора Y, заданного при значениях аргумента, представленных в векторе X, и выдает значения интерполирующей функции в виде вектора Yi при значениях аргумента, заданных вектором Xi.
Ниже приведен текст файл-программы для сравнения различных способов интерполирования, выполнение которой приводит к появлению графиков, изображенных на рис. 6.7:
>> x=[0.1 0.3 0.4 0.6 0.9 1.2];
>> y=[4 4.5 2 -2.9 -0.9 -0.2];
>> plot(x,y,'ko')
xi=[0.1:0.01:1.2];
y1=interp1(x,y,xi,'nearest');
y2=interp1(x,y,xi,'linear');
y3=interp1(x,y,xi,'spline');
hold
Current plot held
>> plot(xi,y1,'k',xi,y2,'k:',xi,y3,'k-.')
legend('table','nearest','linear','spline',4)
grid on
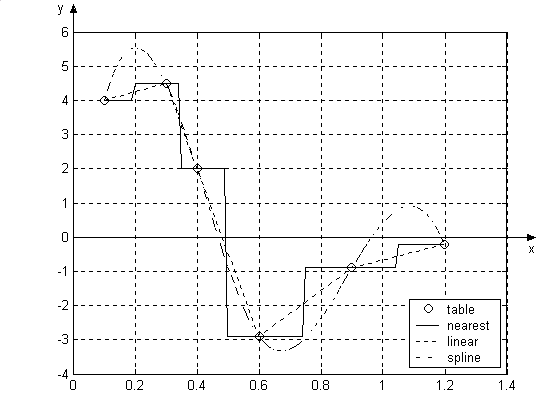
Рис. 6.7