Количество членов выборки с заданным конкретным значением/Объем выборки

Или

f=М/N,

где М – количество элементов выборки с заданным конкретным значением.

Из выше приведенного примера рассчитаем относительную частоту встречаемости дней госпитализации со значением 4,5

f=5/(1+2+3+3+4+5+3+2)=5/23=0,2174

Относительная частота встречаемостипо количеству дней госпитализации со значением 4,5 дня равна 0,22, если это значение выразить в процентах, то получается 22%.

Т.е. 22% от всех участников эксперимента были выписаны спустя 4,5 суток после начала лечения

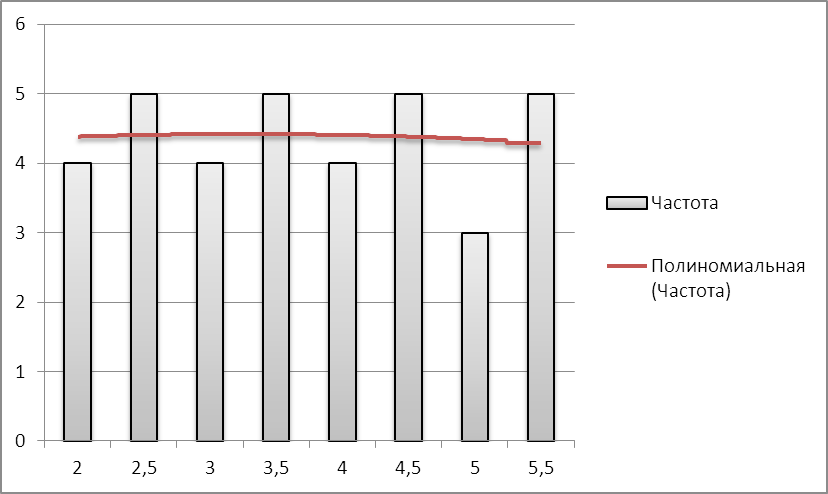
Подсчитав все относительные частоты можно получить следующую таблицу:

Количество дней	Частота встречаемости	Относительная частота встречаемости	Относительная частота встречаемости (%)
2	1	0,0435	4,35 %
2,5	2	0,0870	8,70 %
3	3	0,1304	13,04 %
3,5	3	0,1304	13,04 %
4	4	0,1739	17,39 %
4,5	5	0,2174	21,74 %
5	3	0,1304	13,04 %
5,5	2	0,0870	8,70 %
Сумма:	23	1	100 %

Построим гистограмму:

Изобразим график распределения:

Смысл использования относительных частот встречаемостизаключается в том, что довольно часто необходимо выразить количество членов выборки с разными значениями исследуемого признака в процентном соотношении, или иными словами указатьвероятность возникновенияпризнака с таким значением (в рассмотренном примере значения являются дискретными) уже в генеральной совокупности, при условии, что выборкарепрезентативна.

Также обратите внимание, что суммаотносительных частот равна 1, а их процентного соотношения соответственно 100%.

Забегая вперед, следует сказать, что площадь под кривой распределения всегдаравна 1 (естественно, если при этом используется выражениечастоты встречаемостипризнака в видеотносительной частоты встречаемости).

Также: площадь ограниченной области под кривой распределения равна доле и вероятностипоявленияпризнака с заданными значениями. Т.е. исходя из рисунка, доля членов выборки со значениями в интервале от 4,0 до 5,0 равна площади заштрихованной области на графике.

Далее, если принять, что рассматриваемая случайная величина (признак исследуемого объекта) непрерывна, то увеличивая количество измерений и при этом уменьшая размер интервалов (карманов) мы получим следующие графики (графики соответствуют идеальному случаю нормального распределения):

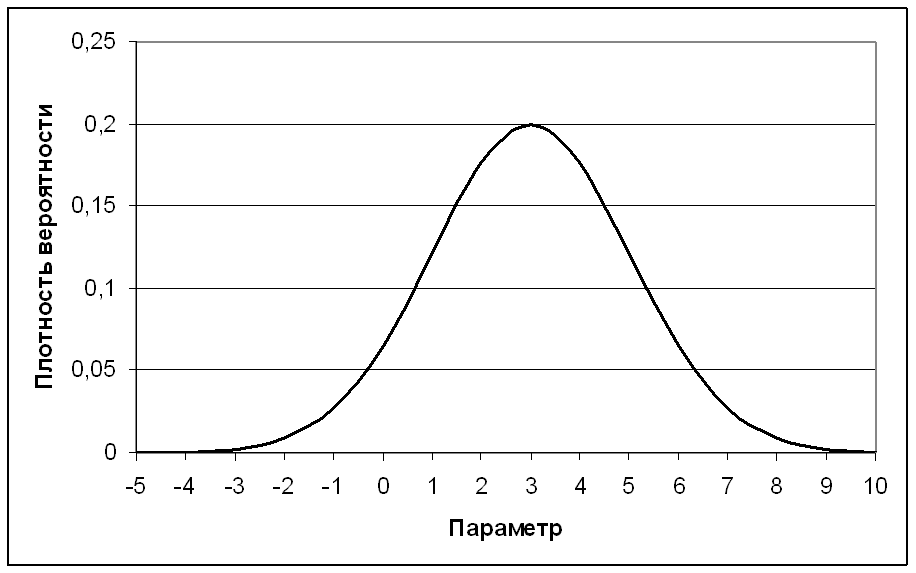
Виды распределения

В большинстве случаев в медико-биологических исследованиях встречаются следующие виды распределения:

• Нормальное

• Ассиметричное

• Равномерное

• Полимодальное

Нормальное (колоколообразное, гауссово) распределение

Нормальное распределение подразумевает, что большая часть значений признака находится в районе так называемого среднего значения (на графике это значение обозначено греческой буквой мю µ).

При нормальном распределении наиболее часто в выборке встречаются значения близкие по величине к среднему по выборке и располагающиеся симметрично ему (значений больше среднего и значений меньше среднего приблизительно одинаковое количество). Или если выражать в процентном соотношении (используя относитльные частоты встречаемости), то можно говорить, что наибольший процент значений признака находится в районе среднего значения, тогда как всего несколько процентов – по краям кривой

При изучении распределений как теоретической базы статистических заключений наибольший интерес представляет площадь под нормальной кривой. Эту площадь можно представить как интеграл от функции f(x).

Как было сказано выше площадь под кривой распределения всегда равна 1 (при выражении частоты встречаеости в виде отьносительных значений), а площадь ограниченная какими-то значениями признака соответствует вероятности или доле.

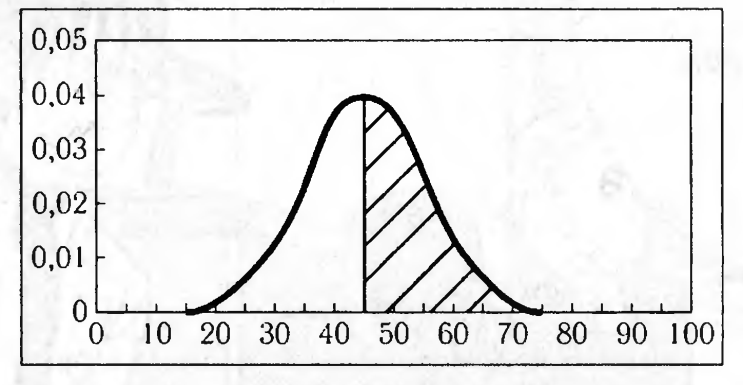
На графике изображено распределение случайной величины. Оно соответствует нормальному распределению, если разделить область под кривой пополам, то обе половины будут равной площади равной 0,5, отсюда можно говорить, что вероятность возникновения значений признака больших 45 (согласно графику) равна 0,5, следоватльно доля членов выборки со значением больше 45 также равна 0,5 (т.е. половине все членов выборки).

Если же мы захотим узнать какая вероятность возникновения признака со значениями больше 65, то изобразив это на графике:

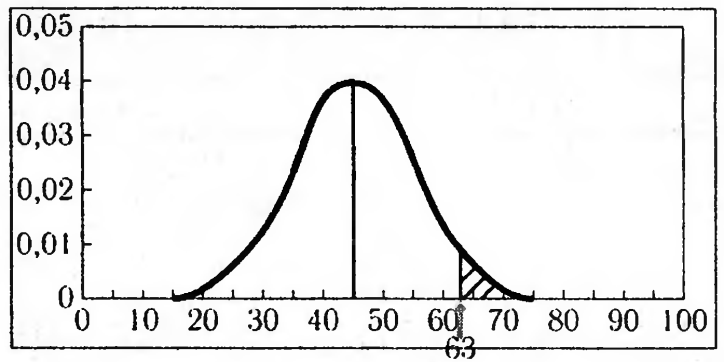
видно, что доля таких членов выборки существенно меньше и вычислив площадь под кривой получим около 3,5%, соответственно меньше 65 равна 100%-3,5%=96,5%

Равномерное распределение

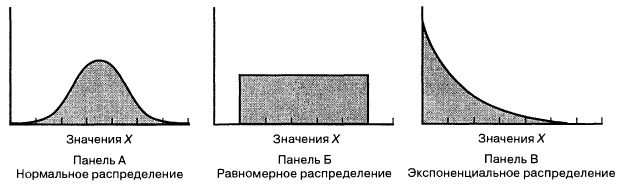
Равномерное распределение указывает на малое влияние переменной на исследуемый процесс или малое влияние процесса на снимаемые показатели.

Ассиметричное (если ассиметрия левосторонняя – логнормальное распределение)

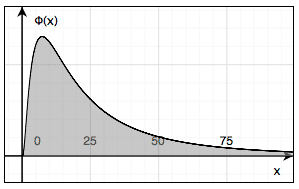
Если функцию f(x) логнормального распределения преобразовать на ее логарифм log(f(x)), то в этом случае полученная функция будет иметь нормальное распределение и характеризоваться теми же параметрами.

Используя графическое представление такой случай можно продемонстрировать следующим образом:

Теперь если рассчитать логарифм десятичный от х, и построить распределение получившихся значений, то мы получим следующий график:

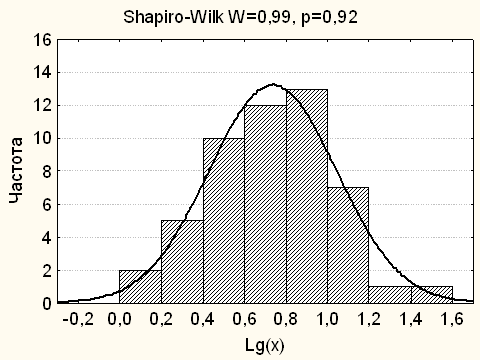
Соответствующий нормальному распределению.

Полимодальное распределение

Полимодальное распределение может быть обусловлено действием нескольких скрытых факторов. Или о, возможно, неправильном построении исследования, например, выборка не является достаточно репрезентативной.

В зависимости от типа распределения выбираются методы статистического анализа

Если распределение является нормальным или логнормальным, то применяют методы так называемой параметрической статистики.

Ниже приведена краткая общая схема статистических исследований.