Поле двухпроводной линии передачи электрической энергии.

Два параллельных цилиндрических провода радиуса а расположены па расстоянии d ≥ а друг от друга. Длина линии l. Заряд одного про­вода + Q, другого — Q. Диэлектрическая проницаемость окружающей среды ε. Длина линии настолько велика, что искажением поля у концов линии можно пренебречь. Так как заряды влияют друг на друга, то распределение их по поверхности проводов будет неравномерным. Чтобы найти потенциал и напряжённость электростатического поля линии, надо определить такое расположение двух фиктивных заряженных осей, при котором поверхность проводов линии совпадает с соответствующими эквипотенциальными поверхностями этих осей. Поле вне проводов такое же как поле заряженных осей. Внутри проводов электростатического поля нет. Пользуясь формулой и учитывая , что x1=0,5, R=a; τ=Q/l, можно найти расстояние ∆ между геометрическими осями проводов и фиктивно заряженными осями

И потенциал любой точки М (x, y)

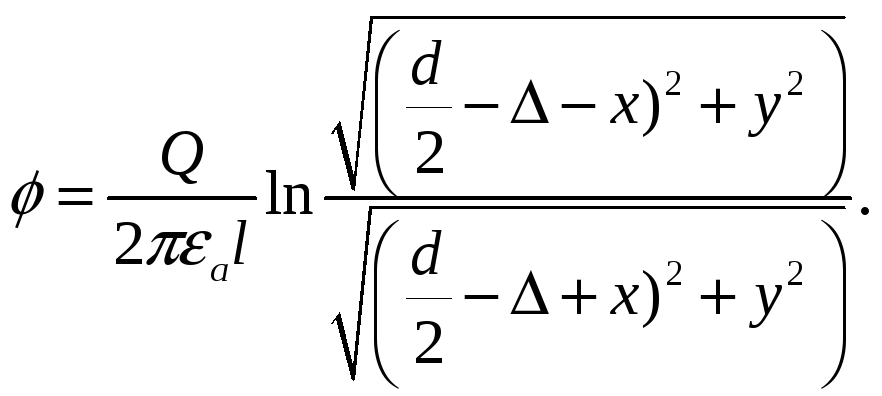
Емкость коаксиального кабеля.

Пользуясь формулой , можно записать потенциал внешнего и внутреннего проводников кабеля:

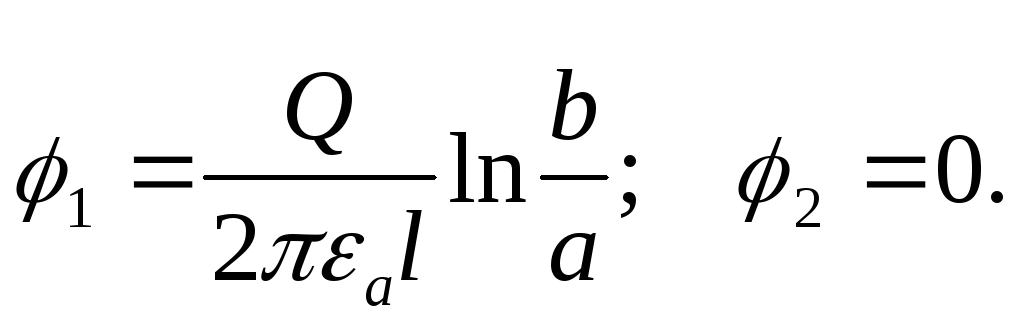
Емкость кабеля будет равна:

Подставив значения постоянных π, ε0 и записав вместо натураль­ного логарифма десятичный, получим формулу емкости единицы длины кабеля, приведенную в § 11-1 ч. I:

Емкость двухпроводной линии передачи электри­ческой энергии.

Так как все точки одного провода в электрическом поле имеют оди­наковый потенциал, то запишем его, пользуясь формулой , для точки А с координатами , y=0, и для точки В с координатами,у=0. Потенциалы этих точек

Следовательно, емкость линии

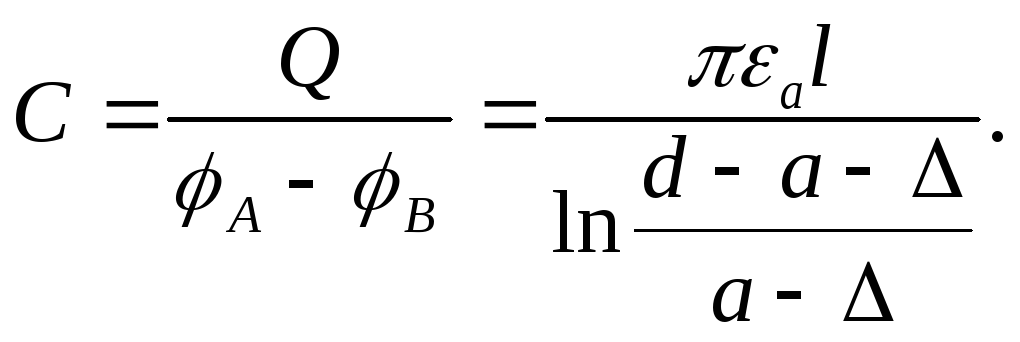
Так как а>>∆, a d >> а, то с достаточной степенью точности емкость двухпроводной линии можно считать равной:

Для воздушноq линии . Подставив значения π, ε0 и заменив натуральный логарифм десятичным, получим формулу емкости еди­ницы длины линии, приведенную :

Электростатическое поле описывается уравнениями Пуассона

и Лапласса

Уравнение Пуассона записывается для области, в которой распре­делены объемные заряды, а уравнение Лапласа описывает поле в остальном пространстве. Интегрирование должно быть выполнено с учетом граничных условии.

Т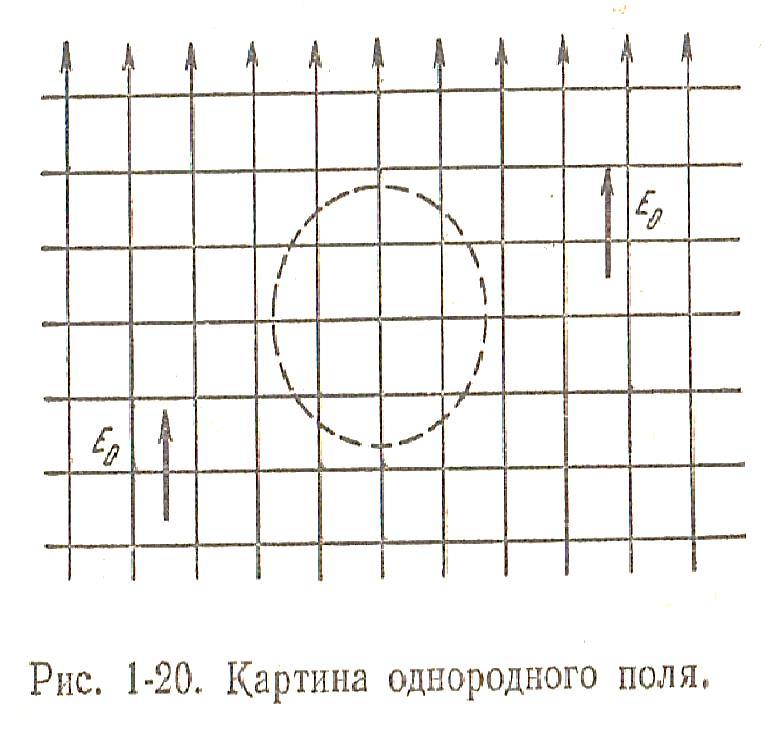очка пулевого потенциала залжется произвольно. В поле объем­ных зарядов напряженность поля Е должна быть конечной величиной.

Рассмотрим следующую задачу.

В однородное электростатическое поле с напряженностью Е0=const помещен металлический шар радиуса а. Шар не заряжен. Диэлектрик, окружающий шар, имеет проницаемость ε. Определить напряженность поля вокруг шара. Начало сферических координат поместим в центре шара. Координату θ будем отсчитывать по часовой стрелке от направления вектора Е0 .

Из соображений симметрии можно установить, что напряженность ноля и потенциал будут зависеть только от двух сферических коорди­нат R и θ. Так как шар металлический, то внутри шара Е=0. Вне шара поле описывается уравнением Лапласа .

Решение этого уравнения будем искать в виде произведения двух функций, одна из которых зависит только от координаты R, другая только от θ.

Чтобы определить эти функции, подставим их произведение в уравнение Лапласса. Получим:

Умножив обе части на R2/f1f2, получим:

Равенство это должно быть справедливо при любых значениях R и θ. Это возможно лишь в том случае, когда каждая из частей уравнения равна некоторой постоянной. Обозначим эту постоянную через k = const.

Уравнение Лапласа разобьется на два уравнения:

Первое уравнение является частным случаем уравнения Лежандра, которое удовлетворяется специальными сферическими функциями, содержащими полиномы Лежандра.

В рассматриваемой задаче искомое решение равно f2 (θ) = cos θ, причем постоянная k2 должна быть равна 2. В этом легко убедиться под­становкой написанного решения в уравнение.

Второе уравнение примет вид:

Введем новую независимую переменную ω так, чтобы R = eω, тогда

Найдём

и

Подставив найденные выражения в решаемое уравнение, получим:

Решение полученного уравнения даст искомую функцию

Корни характеристического уравнения α1=1; α2=-2.

Следовательно,

Окончательное решение уравнения Лапласа примет вид:

Зная потенциал, легко найти и напряжённость поля.

Проекции Е в сферической системе координат

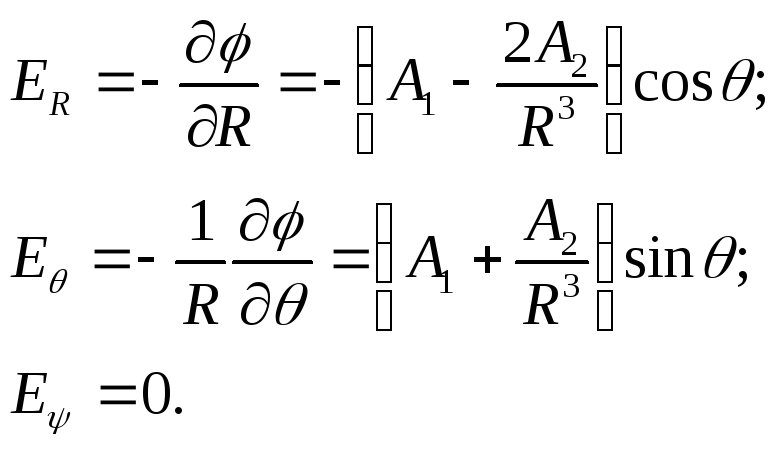
Чтобы найти постоянные интегрирования A1 н А2, необходимо учесть граничные условия. При R=∞ влияние шара не сказывается и Е=Е0, следовательно,

Откуда

Поверхность металлического шара является эквипотенциальной, поэтому φ=const при R = а и всех значениях переменной θ, что возможно только при условии

Следовательно,

Подставив значения A1 и А2, получим искомый потенциал поля

и проекции напряженности электрического поля

Численное значение E равно:

Наибольшая напряженность поля в точке R = а и θ=0

Емакс=3Е0.

Если момент некоторого диполя принять равным

то проекция напряженности электрического поля в рассматриваемой задаче можно записать следующим образом:

Искомое поле получится наложением двух полей, однородного с напряженностью

и поля диполя с моментом р и напряжённостью

Металлический шар, вне­сенный в однородное элект­рическое поле, меняет кар­тину поля так, как изменил бы ее диполь с моментом р, внесенный в то же поле.

Найдем плотность заря­дов, индуцированных на по­верхности шара. Согласно граничному условию (1-18)

Поверхностная плотность заряда

На одной половине шара индуцируется положительный заряд, на другой — равный ему по величине отрицательный заряд:

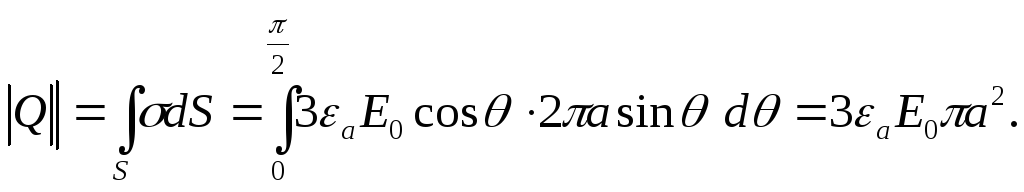
Если положить, что заряд эквивалентного диполя равен этой ве­личине, то плечо диполя