7.2.3. Включение катушки индуктивности к источнику синусоидальной э.Д.С.

1.

2.

3. , где

4. ;;

5. ;

6.

7.

Примечание

1. Начальное значение свободного тока (и характер переходных процессов) зависит от момента включения (начальной фазы ).

Если , т.е., то, т.е.коммутация не повлечет за собой переходный процесс.

Если , т.е., томаксимально и равно.

2. При неблагоприятных условиях коммутации и постоянной времени цепимаксимальное значение переходного тока может достичь почти двойной амплитуды установившегося тока (через время после коммутации).

7.2.4. Заряд конденсатора от источника постоянного напряжения

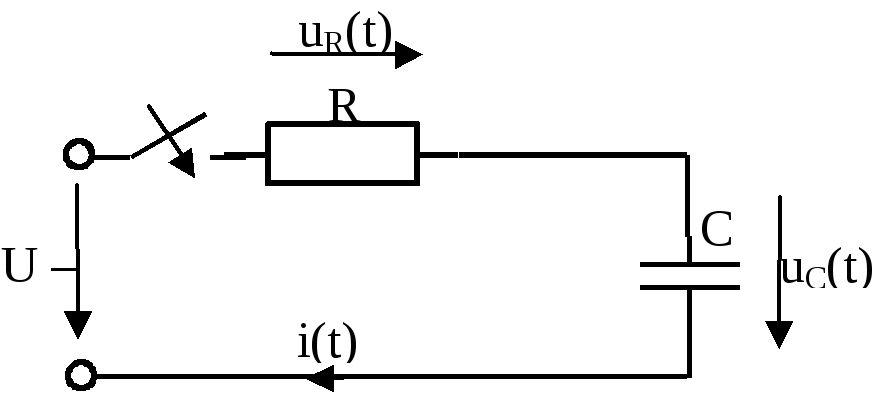
1. ;

;

2.

3.

4.

;;

5. ;

6. ;

;

;

Начальные условия– значения токов через катушки индуктивности и напряжений на конденсаторах, известные из докомутационного режима.

Значения uиiна всех элементах схемы при–зависимые начальные условия. Они определяются из независимых с помощью исходного диф. уравнения.

7.

Примечание

При включении ток изменяется скачком от 0 до и при небольшом активном сопротивлении цепи может достичь больших значений, значительно превышающих номинальное (например, при подключении нагрузки через кабель, распределенная емкость которого велика, а сопротивление проводов низкое).

7.2.5. Разряд конденсатора на резистор

1. ;;

;

2.

3.

4.

;

5.

6.

7. ;

;

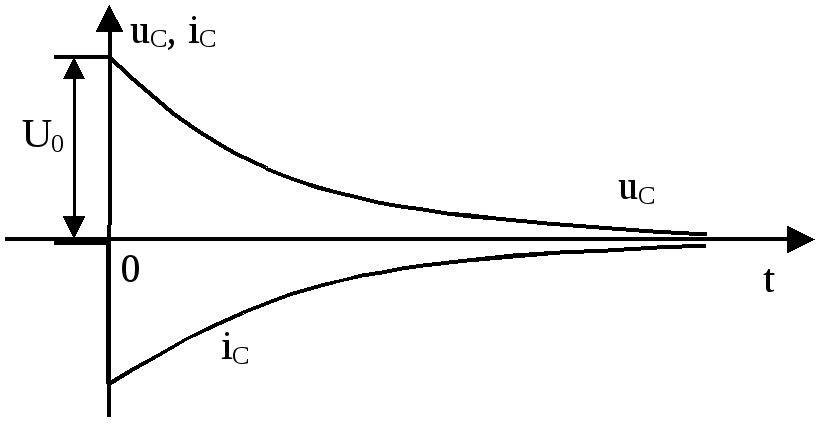
7.2.6. Подключение конденсатора к источнику синусоидального напряжения

1.

2.

3.

4.

5.

6. ;

7. ;

Примечание

1. Если , то переходный процесс не возникает, и сразу же наступает установившейся режим.

2. Если включение происходит при , то свободная составляющая напряжениянаибольшая. Если, то в начальный момент происходит большой всплеск тока, намного превосходящий амплитуду тока. Однако такой большой ток протекает незначительную часть периода, т.к., а потому  <<T.

7.2.7. Разряд конденсатора на rl-цепь

1.

;

где – коэффициент затухания;

– собственная частота контура (резонансная)

2.

3.

4.

5. ;

6.

;;

;

.

Для определения постоянных интегрирования в уравнениях n-го порядка находят начальные значения искомого тока (напряжения) и всех их производных до (n-1) включительно, используя уравнения цепи и начальные значения токов в катушках и напряжений на конденсаторах, определяемых по законам коммутации.

Т.к. здесь n=2, то необходима первая производная:

; .

Из уравнения цепи:

;

.

Т.о.

;

7. ;

;

.

Характер процессов при разряде конденсатора оказывается существенно различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными, что определяется соотношениями между параметрами R,Lи С.

Случай 1:

, т.е.или.

Оба корня p₁ иp₂отрицательны, вещественны и отличны друг от друга:

; ;и.

При изменении tот 0 довеличиныубывают от 1 до 0, причем так как( т.е.), товсегда положительно.

Следовательно, ток iне меняет своего направления, и конденсатор все время разряжается.

Такой односторонний разряд конденсатора называют апериодическим разрядом.

Ток достигает максимума при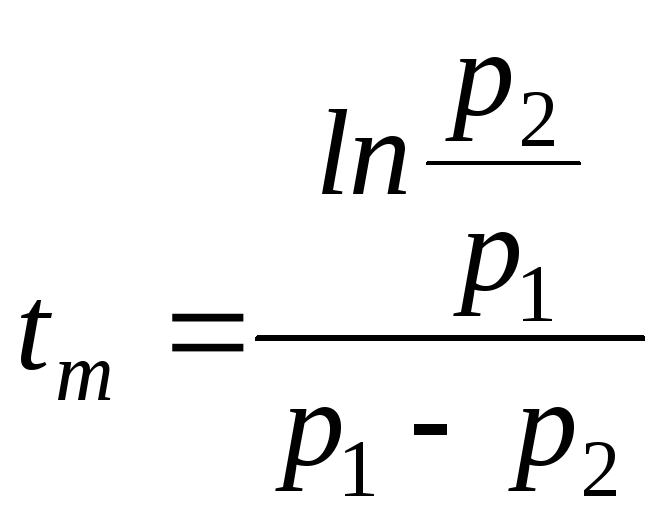, а затем убывает.

Напряжение на емкости монотонно убывает, стремясь к нулю. При расчете использованы условно положительные направления тока и напряжения. Действительные направления показаны на схеме пунктиром и представлены на рисунке (см. выше).

Из уравнения следует, что каждое мгновение:

.

При t= 0.

При t=t_m.

При t>t_mток уменьшается,меняет знак.

С энергетической точки зрения при t<t_mкатушка индуктивности запасает энергию от конденсатора, а приt>t_m– отдает.

Случай 2:

, т.е.или.

Тогда .

Тогда – неопределенность. Раскрыв по правилу Лопиталя получим:

;

;

.

Процесс – апериодический .

Данный случай при являются предельным случаем апериодического разряда, так как при дальнейшем уменьшенииразряд становится колебательным.

Случай 3:

, т.е.или.

Корни комплексно сопряженные:

;

,

где – угловая частота затухающих колебаний.

Тогда ,

где ;;

;.

Для тока:

;

;;

;.

Процесс колебательный.Ток и напряжения на всех участках периодически меняют знак. Амплитуда колебаний убывает по показательному закону –затухающие колебанияс угловой частотой;.

При ;;– формула Томпсона – незатухающие колебания с периодом;– резонансная (собственная) частота контура. При этоми в цепи устанавливается режим, полностью соответствующий установившемуся процессу в нем при резонансе.

Энергетические процессы:

От 0 до t₁=t_m – ток возрастает и режим соответствует апериодическому, т.е. L накапливает энергию,Rрассеивает,Cотдает.

От t₁доt₂–

–Cотдает;

–Lотдает;

–Rрассеивает.

От t₂доt₃– конденсатор С полностью разрядился, ток, поддерживаемый э.д.с. самоиндукции, продолжает протекать в том же направлении и заряжает конденсатор. Энергия магнитного поля частично переходит в энергию электрического поля конденсатора и частично превращается в теплоту на сопротивленииR. К времениконденсатор С заряжается максимально. В этот момент i = 0.

В следующую половину периода процессы повторяются, но знаки напряжений и тока поменяются на противоположные. Таким образом, в зависимости от соотношения параметров возможны следующие режимы разряда конденсатора: