Кучи (heap )

►это абстрактный тип данных, предназначенный для представления взвешенных множеств, имеет свойство - ключ элемента превосходит ключи его потомков.

Множество называется взвешенным, если каждому его элементу однозначно соответствует число, называемое ключом или весом.

Область использования

►сортировка элементов массива ►задачи поиска на графах ►и другие.

Бинарная куча (binary heap)

►Множество, обладающее определенными свойствами упорядоченности:

- нулевой элемент множества – корень

-для каждого элемента множества по

индексу можно определить левую и правую

дочерние вершины

- значение предка должно быть больше потомков

Представлено в виде сортирующего дерева

Сортирующее дерево

►Бинарная куча == ►очередь с приоритетами == ►сортирующее дерево

►Для формулировки этих свойств представим массив А[0], A[1], …A[N- 1] ввиде бинарного дерева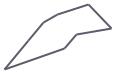

Бинарная куча, состоящая из 10

элементов

каждая вершина: ►ключ (key) ►информационное поле

Основное свойство кучи

►Элементы, хранящиеся в куче, должны обладать основным свойством кучи: для любого i из массива {1, 2, … N-1} существует

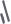
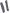
A[HeapParent(i)]>=A[i] ► (i неравно 0).

Свойства

►Размер кучи - это количество вершин в ней

►Высота вершины дерева (максимальная глубина) – высота поддерева с корнем в этой вершине (число ребер в самом длинном пути с началом в этой вершине вниз по дереву к листу)

►вкуче все уровни кроме последнего

заполнены ►Высотадерева = высота корня

►N – число элементов

h log2 N

Основные операции

►Проверка основного свойства кучи Heapify

время работы - O(logn)

►Построение кучи из произвольного массива

BuildHeap - O(n)

►Сортировка массива без использования дополнительной памяти SortHeap -O(nlogn)

► Извлечение наибольшего (очередь с приоритетами) ExtractMax - O(logn)

►Мах - O(1)

►Добавление элемента InsertHeap - O(logn)

Процедура Heapify

►выполняет перестановки между элементами массива

►A[i],

►A[HeapLeft(i)],

►A[HeapRight(i)]

►Сложность T(N) = Ө(i) + T(k), где

► Ө(i) - сложность фиксированной части, T(k) - сложность обработки следующего поддерева.