
Информатика в техническом университете / Информатика в техническом университете. Компьютерная графика
.pdf
3.2. Параметрические кубические кривые
ских полиномиальных кривых, которые задаются на значениями концевых точек и величинами касательного вектора. Обозначим Р\, РА — значения кривой на концевых точках сегмента, a R\, R$— значения касательного вектора в начале и конце сегмента. Удобнее использовать такую нумерацию вместо последовательной, так как далее номерами 2 и 3 обозначаются внутренние точки сегментов кривых.
Для определения базисной матрицы Mh кривой Эрмита, которая связана с геометрическим вектором G/, полиномиальных коэффициентов, запишем четыре уравнения (по одному на каждое геометрическое условие) и, решив полученную систему, найдем значения неизвестных величин.
Запишем компоненту х геометрической матрицы Эрмита в следующем виде:
Чх
и из уравнения (3.2) найдем x(t):
|
3 |
2 |
|
|
3 32 |
2 |
|
h |
|
v |
|
x(t)= |
axt |
+bj |
+cxt+dx= |
|
= t[t ,t |
,t,\] |
xM |
x G |
|
(3.4) |
|
Ограничения в начальной и конечной точках интервала могут быть записа- |
|||||||||||
ны в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х(0) = Р]х= [0,0,0, |
x |
|
|
|
|
|
|
|
|
|
|
x(l) = P4x=[l, I, 1, |
№hGhx. |
|
|
|
|
|
|
|
Найдем производную от уравнения (3.4): |
|
|
|
|
|
|
|
||||
|
|
|
at |
= [3t2, 2t, I, |
0]MhGh x . |
|
|
|
|
|
|
С помощью этого уравнения запишем значения, которые принимает касательный вектор на границах интервала:
=[3, 2, 1, 0]xMhxGh .
dt
Четыре уравнения х(0), х(1), |
, использующие граничные |
dt ' dt J |
условия, можно записать в более компактном матричном виде:
185
3. Математические модели геометрических объектов
Г\х |
0 0 |
|
|
1 |
1 |
|
0 |
1 |
|
2 |
1 |
Из этого уравнения легко найти значение матрицы Mh:
О О О |
-1 |
'2 |
_2 |
1 |
1 |
|
|
||||||
1 1 |
1 |
|
-3 |
3 |
-2 |
-1 |
о о |
1 |
|
О |
О |
1 |
О |
3 2 |
1 |
|
1 |
о |
О |
О |
(3.5)
(3.6)
Полученное значение можно использовать для определения величины x(t). Для этого достаточно воспользоваться соотношением
x(t)=TxMhxGhx,
которое позволяет вычислить искомую величину по известным значениям геометрического вектора Gh . Следуя приведенной схеме, можно найти выражения
для координат y{t) и z(t):
y(t)=TxMhxGhy; z(t)=TxMhxGhz.
Используя три последних уравнения, можно записать компактное матричное выражение для уравнения кривой:
,z(t)]=TxMhxGh;
(3.7)
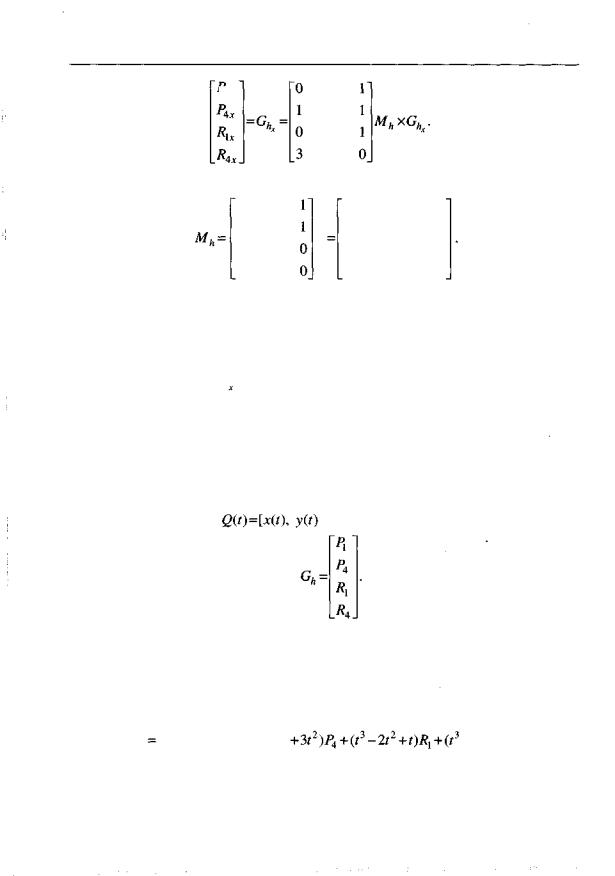
Напомним, что Р\, Р4 — значения кривой в концевых точках; /?ь R4 — значения касательного вектора на границах интервала; Gh — геометрический вектор. Если в уравнении (3.7) раскрыть подвыражение Тх Mh, то можно определить стыковочную функцию Эрмита Bh в явном виде:
Q{t)=TxMhxGh=BhxGh |
= |
(2t3 -3t2 +Щ +(-2t3 |
(3.8) |
~t2)R4. |
На рис. 3.8 показаны графики четырех стыковочных функций, используемых в кривых Эрмита в качестве весов элементов геометрического вектора. На ри-
186
3.2. Параметрические кубические кривые
сунке они помечены именами начальных условий, вклады которых регулируют. Так, функция
fit) = 2t —3t +1, которая задает удельный вес
Р\, фигурирует под этим именем.
В начальной точке it = 0) только одна кривая Pi отлична от нуля. В начальной точке на форму кривой Qit) оказывает влияние только одна кривая Р]. С ростом параметра t влияние функций R], R4, PA становится все более заметным.
Введем обозначения:
/(О
Рис. 3.8. Стыковочные функции Эрмита
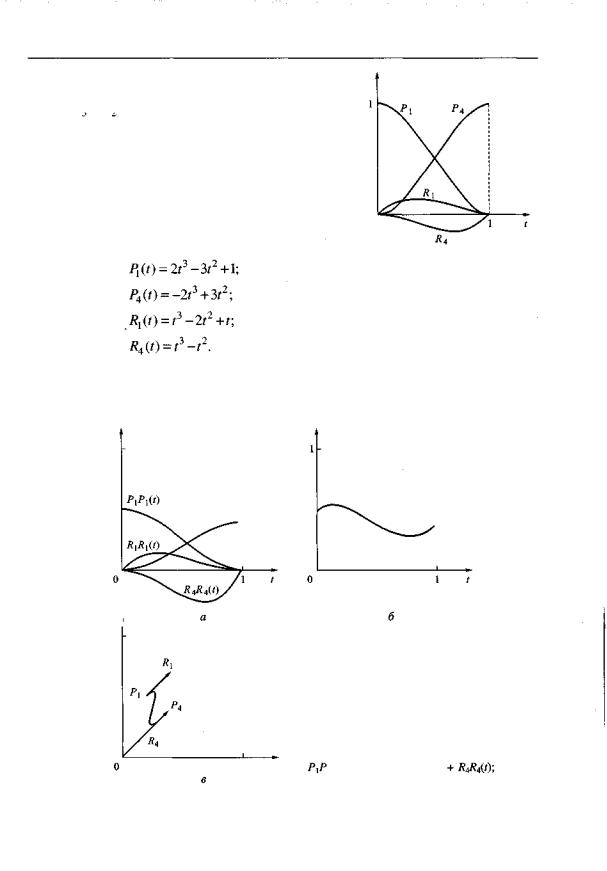
На рис. 3.9 представлены стыковочные функции, взвешенные значениями геометрического вектора (рис. 3.9, а), их сумма (рис. 3.9, б) и результирующая кривая Qit) (рис. 3 9, в).
y(t) |
y(t) |
1 |
|
p4p4(t)
уЩ l
Рис. 3.9. Элементы плоской кривой Эрмита:
а — стыковочные функции; б — сумма стыковочных функций y(t) =
1 x(t) = |
,(0 + P4P4W + RiRi(f) |
|
в — результирующая кривая |
187
3. Математические модели геометрических объектов |
||
y(t) |
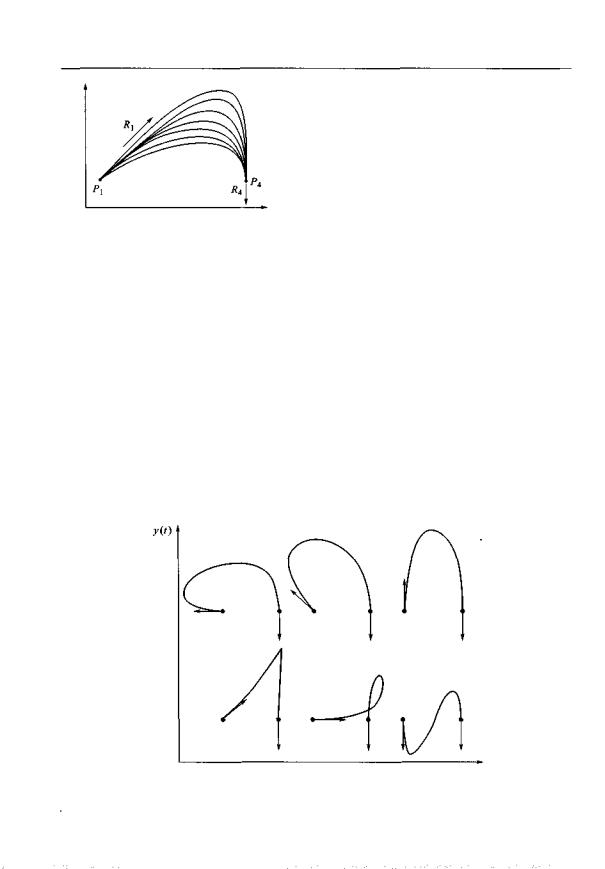
Семейство кривых Эрмита изображено на |
|
|
рис. 3.10. Различная форма кривых продуци- |
|
|
руется вариациями длины касательного векто- |
|
|
ра R\. Направление этого вектора и остальные |
|
|
величины, влияющие на форму кривых, оста- |
|
|
ются без изменения. |
|
|
На рисунке видно, что чем длиннее ка- |
|
x(t) |
сательный вектор, тем большее влияние он |
|
оказывает на форму кривой. |
||
|
||
Рис. 3.10. Семейство кривых Эрмита |
На рис. 3.11 показано еще одно семейст- |
|
во кривых Эрмита, полученное в результате изменения направления касательного вектора одной длины. Если провести дополнительные эксперименты с кривыми Эрмита, то можно заметить еще одну закономерность. Чем меньше длина касательного вектора, тем более спрямленную форму имеет кривая.
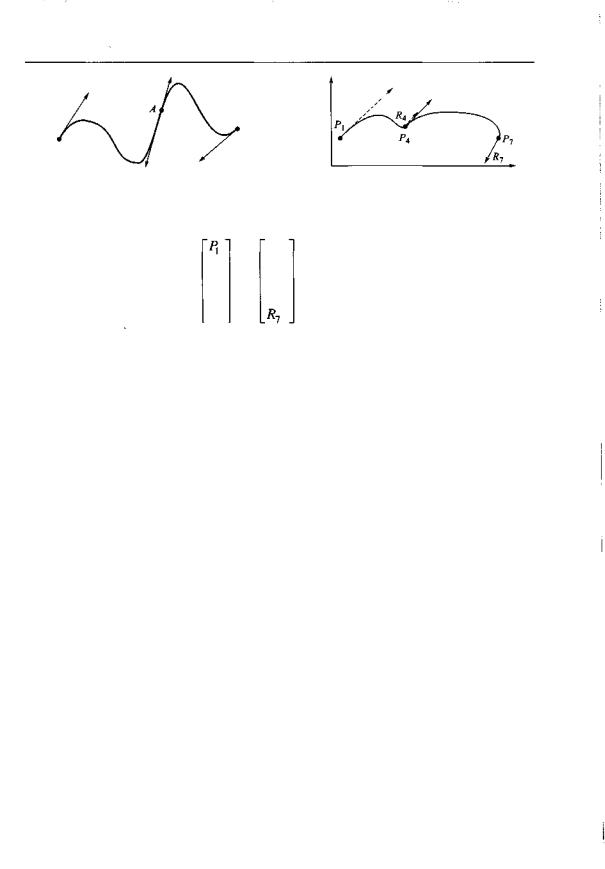
Многие интерактивные графические системы позволяют управлять формой кривых Эрмита интерактивно, посредством настройки положения концевых точек и величин касательных векторов (рис. 3.12). Эти объекты выводятся на экране дисплея и выполняют функции регуляторов формы. Оператор может при помощи мышки перемещать концевые точки и буксировать окончания касательных, программа отслеживает сделанные изменения, рассчитывает и рисует новую форму кривой. Гладкость точки сочленения фрагментов (точка Л на рис. 3.12) обычно задается специальной командой, по умолчанию окончания касательных и точка сочленения являются коллинеарными.
Если две кубические кривые Эрмита соединяются в концевой точке класса G1 (рис. 3.13, точка Р4), то их геометрические векторы должны иметь вид
О |
дс(О |
Рис. 3.11. Семейство кривых Эрмита
188
3.2. Параметрические кубические кривые
y(t)
* 1 /
О x(t)
Рис. 3.12. Интерактивное управление фор- |
Рис. 3.13. Пример соединения двух фраг- |
мой кривой Эрмита |
ментов кривых Эрмита класса G1 |
РА |
|
РА и PI |
при к > О, |
kR4 |
|
А.
т. е. они обязаны иметь общую точку (Р4) и касательные векторы, по крайней мере, с равными направлениями. Более строгие ограничения накладывает принадлежность к классу С\ В этом случае к=1, поэтому в точке сочленения должны совпадать направления и значения касательных векторов смежных сегментов.
С точки зрения визуализации кривые Эрмита очень просты в обработке. Для этого достаточно воспользоваться основным уравнением (3.8). Интервал изменения параметра t делится на несколько частей, после чего вычисляется последовательность значений полинома непосредственно по формуле определения. Для выполнения искомых расчетов существует очень компактный программный код. Эффективность вычислений можно повысить за счет использования схемы Горнера разложения полиномов:
f(t)=at3 +bt2 +ct+d=((at+b)t+c)t+d.
Поскольку кубическая кривая представляют собой линейную комбинацию элементов геометрического вектора (3.3), то можно использовать рациональную стратегию преобразования кривых. Вместо обработки кривой как последовательности сегментов целесообразно выполнить искомое преобразование над элементами геометрического вектора, а затем построить трансформированную кривую. Этот подход оказывается работоспособным для операций поворота, масштабирования и переноса.
3.2.3. Кривые Безье
Рассмотренные в предыдущем разделе методы представления кривых дают хорошие результаты. Они очень удобны при описании формы, основа которой получена с помощью экспериментов или математических расчетов. Это может быть фюзеляж или крыло самолета, некоторые фрагменты двигателя внутреннего сгорания, многие стандартные механические детали и т. д. Существует, одна-
189
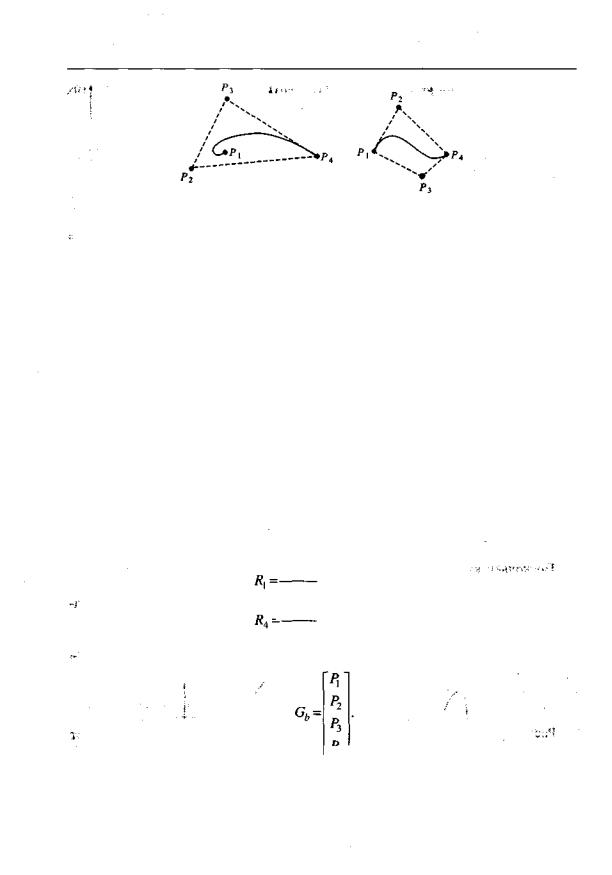
3. Математические модели геометрических объектов
Рис. 3.14. Примеры кривых Безье и положение их контрольных точек
ко, и другой класс задач, когда решение зависит как от функциональных, так и от эстетических требований. Многочисленные примеры таких поверхностей можно найти в любых отраслях дизайна и художественного проектирования, например корпус автомобиля, формы посуды, мебели и т. п. Кроме количественных критериев здесь требуется учет предпочтений дизайнера, и часто необходимо интерактивное вмешательство проектировщика.
Кривые Эрмита не очень удобны для интерактивной работы с кривыми. Направление и величина касательных не дают необходимого интуитивного представления о кривой, так как неочевидна связь между набором чисел и формой соответствующей кривой. Французский исследователь Пьер Безье (P. Bezier) предложил другой метод создания кривых и поверхностей любой формы.
Кривые Безье — специальный вид кубических полиномиальных кривых, у которых для определения положения касательных векторов используются специальные контрольные точки, не принадлежащие самому объекту. На рис. 3.14 пунктиром обозначены выпуклые оболочки контрольных точек. В общем случае выпуклая оболочка может и не касаться всех контрольных точек.
Начальный R\ и конечный R4 касательные векторы кривой Безье зависят от векторов Ри Р2 и Рз, РА, где все Р, — радиусы-векторы, соединяющие контрольные точки с началом координат. Эти величины задаются следующими соотношениями:
СИ |
dQ{0) |
=3(/>2-P1); |
|
dt |
(3.9) |
||
|
|||
|
|
||
О" |
dt |
=3(P4 -P3 ). |
|
I |
Геометрический вектор кривой Безье имеет вид |
||
|
|||
атом:.'
LMJ
Обозначим через МИь матрицу, которая задает соотношение между геометрическим вектором Эрмита и геометрическим вектором Безье. Она определя-
190
3.2. Параметрические кубические кривые |
|
|||||
ется соотношением Gh = Mh x Gb, которое в развернутом виде имеет следую- |
||||||
щий вид: |
|
|
|
|
|
|
1 |
0 |
0 |
0" |
Pi |
|
|
0 |
0 |
0 |
1 |
Pi =MhbxGb. |
(3.10) |
|
-3 |
3 |
0 |
0 |
|||
Рг |
|
|||||
|
|
|
|
|
||
0 |
0 |
-3 |
3 |
p4 |
|
|
Для нахождения базисной матрицы Мь воспользуемся уравнением для кри-
вых Эрмита |
|
|
*•• |
Q(t)=[x(t), y(t), z(t)]=TxMhxGh, |
а |
в котором заменим Gh |
на Mh Gb и представим Мь в виде MbMh |
, тогда |
Q(t)=Tx MhxGh= Tx Mhx(Mhb xGb) = Тх |
(MhxMh) xGb |
= |
TxMbx Gb. |
|||
Выполнив матричное умножение, получим |
|
|
|
|
||
|
|
3 |
-3 |
1 |
|
|
|
3 |
-6 |
3 |
0 |
|
(3.11) |
|
-3 |
3 |
0 |
0 |
|
|
|
|
|
||||
|
1 |
0 |
0 |
0 |
|
|
Окончательно имеем |
|
|
|
|
|
|
|
|
|
|
|
|
(3.12) |
Четыре полинома, которыми взвешены ко- |
|
|
|
|
||
ординаты геометрического вектора в уравне- |
|
|
|
|
||
нии (3.12), называются полиномами Берн- |
|
|
|
|
||
штейна (базисом Бернштейна) (рис. 3.15). По |
|
|
|
|
||
внешнему виду этих полиномов легко оценить |
|
|
|
|
||
влияние контрольных точек на результирую- |
|
|
|
|
||
щую форму кривой Безье. При t = 0 только В] |
|
|
|
|
||
отличен от нуля, поэтому в этой точке кривая |
|
|
|
|
||
приближается к Pi. Аналогично при t - 1 толь- |
|
|
|
|
||
ко полином В4 вносит свой заметный вклад в |
|
|
|
|
||
поведение кривой, поэтому на форму кривой |
|
|
|
|
||
влияет только положение точки Р4. |
|
Рис. 3.15. Представление поли- |
||||
На рис. 3.16 показаны два сегмента кривой |
||||||
Безье, соединенные общей точкой. Для ее при- |
номов Бернштейна, которые слу- |
|||||
жат весовыми коэффициентами в |
||||||
надлежности классу G1 требуется выполнение |
математическом описании кривых |
|||||
условия |
|
|
|
Безье: |
|
|
|
|
|
|
|
||
Р3-Р4=к(Р4-Р5), |
к>0. |
|
|
В, =(1-03 ; |
B2 |
= 3t(\-t)2; |
191

|
3. Математические модели геометрических объектов |
|
|
|||||
|
*Pl |
|
|
Это значит, что три точки Ръ, Р4, Р5 долж- |
||||
|
^_ 5 |
_ |
рь |
ны отличаться друг от друга, но лежать на |
||||
|
|
|
|
одной прямой. Если коэффициент к = 1, то |
||||
|
|
|
|
дополнительно к непрерывности класса G1 |
||||
pi |
p |
|
pi |
гарантируется |
принадлежность |
кривой |
||
|
->-., * |
|
|
классу С1. |
|
|
|
|
Рис. 3.16. Два сегмента кривой Безье, |
^g- |
полиномы |
двух |
смежных |
||||
|
, |
„ |
„ „ |
Обозначим |
||||
|
соединенные общей точкой Р4 |
. |
. |
, J |
. |
тж |
||
|
|
|
|
сегментов xt (левого) и хг |
(правого). |
Ис- |
||
пользуя введенные обозначения, можно сформулировать условия, которые обеспечивают выполнимость условий С0 и С1 в точке сочленения сегментов:
Применив уравнение (3.12), получим
Как и предполагалось, эти условия выполняются и для двух оставшихся координат у и z. Для экономии места соответствующие выражения опускаются. Таким образом, для выполнимости условий С0 и С1 требуется, чтобы Р4 - Р3 =
=Р5-РА.
Если проанализировать полиномы Бернштейна (й| - В4), то очевидно, что их сумма всегда равна единице, а каждый из них принимает только неотрицательные значения на интервале 0 < t < 1. Таким образом, Q(t) представляет собой взвешенное среднее четырех контрольных точек. Это значит, что каждый сегмент кривой Безье полностью вписан в выпуклую оболочку, форма и положение которой зависит от контрольных точек (см. рис. 3.14). Для двухмерных кривых эту оболочку можно представить как многоугольник, который образует резиновая нить, натянутая на контрольные точки. Для кривых в трехмерном пространстве оболочкой служит полиэдр, образованный подобно многоугольнику.
Свойство выпуклой оболочки сохраняется для всех кубических кривых (не только кривых Безье), определенных как взвешенная сумма контрольных точек, если их веса неотрицательны и в сумме дают единицу. Более того, это утверждение оказывается справедливым и для n-мерного пространства.
Еще один очевидный вывод следует из равенства суммы полиномов единице. Значение четвертого полинома всегда могут быть найдены по известным величинам трех других простым вычитанием из единицы их суммы.
192

3.2. Параметрические кубические кривые
Выпуклые оболочки сегментов можно использовать для эффективного решения задачи отсечения изображения. Вместо того, чтобы определять принадлежность области видимости каждого сегмента кривой отдельно, достаточно рассмотреть их выпуклые оболочки. Если выпуклая оболочка не принадлежит области видимости, то ее сегмент автоматически исключается из рассмотрения. И наоборот, принадлежность оболочки фрагмента кривой влечет за собой включение соответствующего сегмента. Если оболочка пересекает границу области, то для решения поставленной задачи требуется рассмотреть положения самого сегмента кривой.
В заключение раздела приведем краткую сводку основных свойств кривых Безье:
•форма кривой Безье зависит от выпуклой оболочки, образованной контрольными точками кривой;
•первая и последняя точки кривой совпадают с соответствующими точками определяющего многоугольника;
•векторы касательных на концах кривой Безье по направлению совпадают с первой и последней сторонами многоугольника;
•кривая обладает свойством уменьшения вариации. Это означает, что кривая пересекает любую прямую линию не чаще, чем определяющий многоугольник;
•кривая инвариантна относительно аффинных преобразований.
Сматематической точки зрения кривая, заданная вершинами многоугольника, зависит от интерполяции или аппроксимации, устанавливающей связь кривой и многоугольника. Здесь основой является выбор базисных функций. Базис Бернштейна, который порождает кривые Безье, обладает двумя свойствами, ограничивающими гибкость кривых. Ограничение состоит в том, что количество вершин многоугольника жестко задает порядок многочлена. Например, кубическая кривая должна быть задана четырьмя вершинами и тремя отрезками. Многоугольник из шести точек всегда порождает кривую пятого порядка. Единственный способ понизить степень кривой — сократить число вершин, а повысить степень кривой — увеличить их число.
Второе ограничение следует из глобальной природы базиса Бернштейна. Это означает, что величина аппроксимирующих функций В,(?) из уравнения (3.12) ненулевая для всех значений параметра t в интервале от 0 до 1. Любая точка на кривой Безье зависит от всех определяющих вершин, поэтому изменение какой-либо одной вершины оказывает влияние на всю кривую. Локальные воздействия на кривую невозможны.
Поскольку наклон концов кривой Безье задан соответствующими сторонами многоугольника, можно передвинуть среднюю вершину пятиточечного многоугольника, не меняя направления на концах. Вследствие глобальности базиса Бернштейна меняется форма всей кривой. Невозможность внесения локальных изменений не является решающим критерием оценки кривых Безье. Это ограничение преодолевается алгоритмическими и программными средствами. Все пакеты, оперирующие с такими кривыми, разрешают пользователю создать новую
193

3. Математические модели геометрических объектов
вершину в любой внутренней точке сегмента кривой. Это влечет за собой разбиение сегмента на две части и предоставляет дополнительные возможности локального управления формой кривой.
3.2.4. Однородные нерациональные В-сплайны
Термин «сплайн» заимствован из традиционной технологии изготовления поверхностей сложного профиля. Так ранее называли полосы материала, которые под действием грузов выгибались таким образом, чтобы получить искомую конфигурацию сложной фигурной поверхности. Математическим эквивалентом физических сплайнов служат так называемые натуральные кубические сплайны, представляющие собой непрерывные кубические полиномы, форма которых задается п контрольными точками. Кривые этого вида обладают более высокой степенью гладкости, чем кривые Эрмита и Безье. При выполнении некоторых дополнительных условий они могут принадлежать к классам С0, С1 и С2. Однако их применение в системах машинной графики сдерживается двумя недостатками. Вычисление формы натуральных полиномов требует обращения матриц высокого порядка, что затрудняет интерактивную работу с ними даже на мощных вычислительных системах. Кроме того, смещение контрольной точки влечет за собой не локальные изменения формы, а влияет на общую форму кривой. •;•• В-сплайны — совокупность полиномиальных сегментов, положение которых задается небольшим числом контрольных точек. Смещение одной контрольной точки влияет только на некоторый фрагмент кривой и не вносит глобальных изменений в ее форму. В-сплайны обладают такой же гладкостью в точках сочленения, как натуральные сплайны, но значительно превосходят последние по эффективности вычислений.
При обсуждении В-сплайнов немного изменим систему обозначений, принятую в предыдущих разделах. Будем рассматривать эти объекты как интегральные кривые, а не как отдельные сегменты. Сегменты В-сплайнов не обязаны проходить через контрольные точки. Условия гладкости могут передаваться на сегмент со стороны соседних фрагментов.
Кубический В-сплайн задается последовательностью полиномиальных сегментов 2з, Q^--,Qm, положение которых зависит от контрольных точек Ро, Ри Рт, т > 3. Сегменты, образующие кривую, могут быть определены как функции аргумента t на интервале 0 < t < 1, однако удобнее переопределить их таким образом, чтобы они принимали значения на общем последовательном интервале (для этого достаточно выполнить подстановку t - t + к).
Итак, каждый сегмент Qt задан на интервале t, < t < t,•+ ь где 3 «S i < т. Первый сегмент (2з (w - 3) задан на интервале /3 ^ t < и четырьмя контрольными точками Р0- • -Ръ- Для каждого i > 4 между соседними сегментами <2<i и <2, существует точка сочленения или узел, положение которого задается значением па-
194
